Метод интервалов ( для решения всех типов уравнений с модулями).

Л.А. Семенко

 

 

                                                                       

 

(Методические рекомендации из опыта работы в 7 – 9 классах)

Отрадная 2006 г.

 

Уравнения с модулем.  

Основные виды уравнений и способы их решений.

Повторение.

Определение: Модулем (абсолютной величиной) действительного числа х, т.е.‌‌ ‌‌| x |, называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное:

 

‌‌| x |=

Геометрический смысл модуля.

Каждому действительному числу соответствует точка числовой оси, для которой это число является координатой. Абсолютная величина этого числа – это расстояние соответствующей точки оси до начала координат. Например: х = а и  х = – а удалены от начала координат на | а|.

                                         

           – а                     0                      а

               .                      .                     .  х

               |←| а| = |– а| →|← | а|     →|

Геометрически, абсолютная величина, (модуль) действительного числа есть расстояние от точки, изображающей это число на числовой оси, до начала координат.

 

Способы решения простейших уравнений с модулями.

1. | x| = с ( действительное число)

| x | = с      

 Примеры: | x |= 5,   х = ± 5;

              | x |= 0,    х = 0;

              | x |= –5,   х  ø;

2. | f(x)| = b, b>0

    | f ( x )| = b

| f ( x )| = b , или | f ( x )| = – b

Примеры:

а). | x +2 |= 7                              

x +2 = 7  или x +2 = – 7           

x = 5;           x = –9              

                                                       

Ответ: 5 ; –9.

                                                            

 б). | x ² –8 |= 1

x ² –8 = 1 или x ² –8 = –1

x ² =9;           x ² =7

 х_1,2=± 3    х_3,4 = ±

Ответ: ± 3; ± .

в). | x ² – 4х |= 4

x ² – 4х = 4       или x ² – 4х = – 4

x ² – 4х – 4=0;        x ² – 4х + 4=0

х_1,2 =2 ± 2 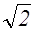;         х_3,4 = 2

Ответ: 2 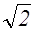± 2 ; 2.

Упражнения для самостоятельной работы:

1. |5 x +1 |=4  | x ² – 4 |= 5  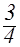          | x –  |=

2. | x – 5 |=4      | x ² – 2х |= 3    | 3– 4х |= 3

3. |2х–5 |= 3 | x ² – 2х |= 1         | x ² – х–1 |= 1  

4. | 3– 4х |= 1 | x ² – 3х |= 2         | x ² –х–5 |=1          

5. | 5– 4х |= 3| x ² + 3х |= 2         | x ² –5х+6|=2

 3. | f(x)| = g(x), g(x) = ≥0.

 

По смыслу модуля это уравнение может иметь решение, если правая часть g ( x ) = ≥ 0 ( неотрицательна ). Значит, раскрывая модуль при g ( x ) = ≥ 0 имеем два уравнения:

f ( x ) = g ( x )   или f ( x ) = – g ( x ). То есть

 

| f ( x )| = g ( x )

 

 Примеры:

а). |2х–3 |= х – 2

х – 2 ≥ 0 х ≥ 2

2х–3 = х – 2 или 2х–3 = – ( х – 2 )

х₁ = 1                     х₂ =

         

                   .     . . .           х

                  0           1      2

Ответ: х  ø

б). |2х–1 |= 5х – 10.

5х – 10 ≥ 0, 5х ≥ 0, х ≥ 2

2х–1 = 5х – 10          или        2х–1 = – (  5х – 10)

2х–5х = 1 – 10                                2х+5х = 1 + 10

–3х = – 9                                      7х = 11

х= 3                                           х =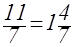

                   .     . . .    .   х

                  0           1      2        3

 Ответ:  х = 3

б). | х–1 |=1 – х²

1 – х² ≥ 0, (1 – х) (1 + х ) ≥ 0, –( х +1)( х–1) ≥ 0,

 ( х +1)( х–1) ≤ 0, –1 ≤ х ≤ 1.

х–1 =1 – х²                или           х–1 = х² – 1

х²  + х – 2 = 0                           –х²  + х = 0

х₁ = – 2                                               х₃ =  0

х₂ = 1                                               х₄ = 1

 

          .     .     .     .   х

          –2        –1      0          1

                        

Ответ:  х = 0; 1.

Упражнения для самостоятельной работы:

1). |х+2 |= 6– 2х                      11).|2х²– 1|= х ²– 2х + 3

2).|3х– 7|=2х + 1                 12).|5– х²|= х²– 7

3).|х– 1|=х + 8                           13).|х²+3х|=1 – х

4).|х+3 |=3(4– х)                           14).|х²+3х– 4|= х ²– 7х – 2  

5).|х²–3х|=4 – х                         15).|х²+3х+2|= (5х +16)

 6). |х²+3х– 10|=3х– 1                16). |х²– 4|=х + 2

 7). |х²–4х– 12|=6– х                   17). |х²–х + 3|= – х – 1

 8). |х²–4х+ 3|=2х–2                   18). |х²+2х–5| = 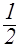(х–1)

 9). |х²–7х+ 12|= х²+8х– 3          19). |3х+3 |= 4– 4х²

10).|х– 1|= 3х²                              20). |х| = 1– х² – 3х  

4. | ± f(x)| = f(x).

Решение данного уравнения равносильно решению неравенства f ( x ) ≥ 0, т.е. | ± f ( x )| = f ( x ) f ( x ) ≥ 0.

Примеры:

а). |х–8 |= х – 8

х – 8 ≥ 0,

х ≥ 8

Ответ: [8; + ∞).

б). |х| = – х.

Это уравнение можно рассматривать как уравнение             

|–(–х)|= – х, поэтому– х ≥ 0, х ≤ 0.

               Ответ:(– ∞; 0].

в). | х² + х–6 |= х² + х–6

х² + х–6 ≥ 0; (х+3)( х–2) ≥ 0

х₁ = –3    х₂= 2

 

                                 .              .                         х

                                    -3                 2

       Ответ:(– ∞; -3]  [2; + ∞).

в). |4х–7 |= 7 – 4х

|–(7 – 4х) |= 7 – 4х;

7 – 4х ≥ 0; – 4х ≥ –7 ; х = , х ≤

                            .                  х

                                         

Ответ:(– ∞; ].

Упражнения для самостоятельной работы:

1). |х–2 |= х – 2               6). | х² –8 х+ 12 |= х² –8 х+ 12

2). |х| =  х = 0                   7). |2 х² –8 х+ 6 |= 2 х² –8 х+ 6

3). 7 – 4х = |4х–7 |           8). |- х² +5 х+ 6 |= х² +5 х+ 6

4). |9 – х² |= 9 – х²             9). | х² – х+ 5 |= х² – х+ 5.

5). х– |х–2 | = 2              10). | х² +х |= х² +х.

  5. | f(x)| = | g(x)|.

Уравнение равносильно двум уравнениям f ( x ) = g ( x ) или f ( x ) = – g ( x ). То есть | f ( x )| = | g ( x )|  

Примеры:

а). |х²–5х+ 7|= |2х– 5|

х²–5х+ 7= 2х– 5            или    х²–5х+ 7= 5– 2х   

х²–7х+ 12=0                                 х²–3х+ 2=0

х₁ = 3                                              х₃ = 2

х₂ = 4                                              х₄ = 1

 

Ответ: 1; 2; 3; 4.

 

б). |х²– 1|=| х + 3|

х²– 1= х + 3                     или      х²– 1=– х– 3

х²– х–4 =0                                    х²+ х+2 =0

D = 17 > 0                               D = – 7 < 0 - корней нет

x _1,2 =

 

Ответ: .

 

в). |х²+5х– 3|= |2х– 1|

х²+5х– 3= 2х– 1    или         х²+5х– 3=1– 2х

D = 25 > 0                                      D = 81 > 0

x _1,2 =                                       x _1,2 =

х₁ =                                                    х₃ =

х₂ = – 2                                              х₄ = –4

 

Ответ: – 2;  ; –4.

Упражнения для самостоятельной работы:

1). | х² +6 х + 8 |= | 7х –6|          7). | 2х –1|=| х +3|

2). | 3х² –5х – 2 |= | х² +6х –16|   8). |х–2 |=| 3х +9|

3). | 2х² –1|=| х²– 2х – 3|           9).  |х–2 |=| 3 –3х|

4). | 2х –3|=| х +7|                     10). |х – х² –1|= | 2х –3 + х²|

5). | х +7|= |х–2 |                      11). | х² +4 х + 3 |= | х +1|

6). | х² –1|= | х +5|                     12). |х–2 |=3| 3 – х|

Способ подстановки ( замены переменной ).

  х² –6| х| + 5 = 0.    по   свойству   х² =| х|²    имеем:

| х|²–6| х| + 5 = 0. Применим подстановку | х| = t ≥ 0, Тогда получим уравнение t ² – 6 t + 5 = 0, t ₁ = 1, t ₂ = 5.

1. | х|=1,  х_1,2 = ± 1;

2. | х|=5, х_3,4 = ± 5

Ответ: –5; – 1; 1; 5.  

Примеры:

а). х² –6| х| + 8= 0.

| х|²–6| х| + 8 = 0.

| х| = у ≥ 0, у ² – 6у + 8 = 0, у₁ = 4, у₂ = 2;

1. | х|=4, х_1,2 = ± 4;

2. | х|=2 х_3,4 = ± 2.

 

  Ответ: – 4; –2; 2; 4.

а). х² +| х| – 2= 0.

| х|² +| х| – 2= 0

| х| = у ≥ 0, у² +у – 2= 0, у₁ = – 2, у₂ = 1;

1. | х|= –2, корней нет

2. | х|=2 х_1,2 = ± 1.

  Ответ:   ± 1.

Упражнения для самостоятельной работы:

1).   х² –2| х| – 3= 0                     9). х² –3| х| = 0

2).   х² –| х| – 2= 0                      10).  х² –| х| + 2= 0                      

3). х² +5| х| + 4= 0                    11).  х² –2| х| + 3= 0

4).  х² –6| х| + 5= 0                     12).  х² –7| х| + 12= 0

5). х² –5| х| + 6= 0                    13). х² –2| х| – 35 = 0

6). х² +| х| + 2= 0                     14). х² –| х| – 6 = 0

7). х² –4| х| + 5= 0                    15). х² –2| х| – 4 = 0

8). х² –3| х| + 2= 0                     16). Х² +7| х| +12= 0

Метод интервалов ( для решения всех типов уравнений с модулями).

Метод интервалов - это универсальный метод решения уравнений всех видов с модулями.

Метод интервалов состоит в том, что область определения уравнения разбивается на промежутки, в каждом из которых все подмодульные выражения сохраняют знак. Для этого достаточно найти корни подмодульных выражений и расположить их в порядке возрастания. Концы полученных промежутков можно относить к любому из смежных промежутков. Раскрыть модули ( входящие в уравнение) на каждом промежутке. Для этого необходимо число из данного промежутка подставить вместо переменной в подмодульное выражение. Определив знак подмодульного выражения, освободиться от модуля. Решить уравнение на каждом промежутке своё и найденные решения объединить в ответе.

 

Примеры:

а). | х–1 |+| х +2|= 1.

 

Найдем корни подмодульных выражений

х – 1 =0, х = 1;

х +2 = 0 , х= – 2.

       

                                .         .               х

                                             –2                1

Решим уравнения на промежутках.

Ι.  (–∞;–2): –х+1–х–2 = 1; –2х – 1 = 1; –2х =2; х = – 1;

 – 1 (–∞;–2); корней нет

ΙΙ.  [–2; 1] ; –х + 1+х + 2 = 1; 0х = –2, решений нет.

ΙΙΙ. ( 1; + ∞ ); х – 1 + х + 2 = 1; 2х + 1 = 1; 2х = 0; х = 0; 0  ( 1; + ∞ ); корней нет.

 

               Ответ: корней нет.

б). |2 х + 1  |+ |5 –3 х |+1– 4х= 0 .

2х + 1 = 0;  2х= – 1;  х = – .

5 – 3х = 0; – 3х= – 5; х =  =

                           .               .             х

                                –                         

Ι.  (–∞;– ): –2х–1+ 5 –3х+ 1 –4 = 0; –9х +5 = 0; х = ;

(–∞;– ); корней нет.

ΙΙ.  [– ; ] ;    2х + 1 + 5 – 3х + 1– 4х = 0  ;   –5х = –7,      х = ,  х =  [– ; ];  - корень уравнения.

ΙΙΙ. ( ; + ∞ ) ; 2х + 1 – 5+ 3х + 1– 4х = 0; х – 3 = 0,     х = 3 ( ; + ∞ ); х = 3- корень уравнения.

                  Ответ: 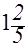; 3.

в). |  х – 1  |+ |х –2 | = 1

х – 1 = 0,  х = 1.

х –2 = 0, х = 2.

                         .     .                  х

                                     1          2

Ι.  (–∞;1) : – х + 1 –х + 2 – 1; –2х + 3 = 1;   – 2х = – 2;

х = 1  (–∞;1), корней нет.

ΙΙ.  [1; 2] ; х – 1 – х + 2 = 1; 0х + 1 = 1; 0х = 0, х – любое число х  из промежутка [1; 2] .

ΙΙΙ. (2; + ∞ ); х – 1 + х – 2 = 1; 2х –3 = 1; 2х = 4;            х = 2  (2; + ∞ ),  корней нет.

 

  Ответ: [1; 2]

 

Упражнения для самостоятельной работы

1). |  х + 4 |– |х –3 |= 1     9). | 2 х + 6 |+|3х +7 |= х – 3

2). |  х |+ |х –1|+ |х –2|= 6  10). |  х–1 |+ | х –2|+ |х –3 |= 4

3). |  х + 4 |+ |х –3 |= 7        11). |х–1|–| х|+ 3|х –1|–|х –2|=х+2

4). |  х |+ |х –1|+ |х –2|= 2 12). |  х + 2 |– | 5 – х  |= –7

5). |  х |– |х –2| = 2            13). |х –4|+ |х +4|= 9

6). |х –3|+|х +2|–|х –4|=3 14). |  х |+ |х –1|+ |х –2|= 6

7). |5–х |+|х +2|=|3–х |     15). |  х–1 |+ | х –2|= |х –3 |– 4

8). |х|–2|х +1|+3|х +2|= 0    16).  х² – |х –2| – 10 = 0