Равнобедренный треугольник

Теорема Пифагора

Задание 15 № 70

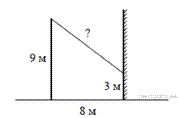От стол­ба вы­со­той 9 м к дому на­тя­нут провод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли (см. рисунок). Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те длину провода.

Задание 15 № 96

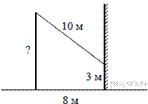От стол­ба к дому на­тя­нут провод дли­ной 10 м, ко­то­рый закреплён на стене дома на вы­со­те 3 м от земли (см. рисунок). Вы­чис­ли­те высоту столба, если рас­сто­я­ние от дома до стол­ба равно 8 м.

Задание 15 № 148

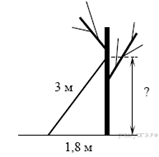Лестницу дли­ной 3 м при­сло­ни­ли к дереву. На какой вы­со­те (в метрах) на­хо­дит­ся верхний её конец, если ниж­ний конец от­сто­ит от ство­ла дерева на 1,8 м?

Задание 15 № 132751

Мальчик про­шел от дома по на­прав­ле­нию на во­сток 800 м. Затем по­вер­нул на север и про­шел 600 м. На каком рас­сто­я­нии (в метрах) от дома ока­зал­ся мальчик?

Задание 15 № 132752

Девочка про­шла от дома по на­прав­ле­нию на запад 500 м. Затем по­вер­ну­ла на север и про­шла 300 м. После этого она по­вер­ну­ла на во­сток и про­шла еще 100 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Задание 15 № 132753

Мальчик и девочка, рас­став­шись на перекрестке, пошли по вза­им­но перпендикулярным дорогам, маль­чик со ско­ро­стью 4 км/ч, де­воч­ка — 3 км/ч. Какое рас­сто­я­ние (в километрах) будет между ними через 30 минут?

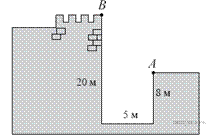
7. Задание 15 № 311509  Глубина кре­пост­но­го рва равна 8 м, ши­ри­на 5 м, а вы­со­та кре­пост­ной стены от ее ос­но­ва­ния 20 м. Длина лестницы, по ко­то­рой можно взо­брать­ся на стену, на 2 м больше, чем рас­сто­я­ние от края рва до верх­ней точки стены (см. рис.). Най­ди­те длину лестницы.

Задание 15 № 311854

Девочка про­шла от дома по на­прав­ле­нию на запад 20 м. Затем по­вер­ну­ла на север и про­шла 800 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 200 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Задание 15 № 311962

Лестница со­еди­ня­ет точки A и B и со­сто­ит из 35 ступеней. Вы­со­та каж­дой сту­пе­ни равна 14 см, а длина — 48 см. Най­ди­те рас­сто­я­ние между точ­ка­ми A и B (в метрах).

Задание 15 № 314845

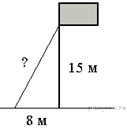Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 15 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 8 м. Най­ди­те длину троса.

Задание 15 № 315106

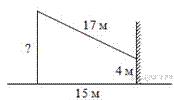
От стол­ба к дому на­тя­нут про­вод дли­ной 17 м, ко­то­рый за­креплён на стене дома на вы­со­те 4 м от земли (см. ри­су­нок). Вы­чис­ли­те вы­со­ту стол­ба, если рас­сто­я­ние от дома до стол­ба равно 15 м.

Задание 15 № 316289

Девочка про­шла от дома по на­прав­ле­нию на запад 880 м. Затем по­вер­ну­ла на север и про­шла 900 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 400 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Задание 15 № 316326

Мальчик прошёл от дома по на­прав­ле­нию на во­сток 400 м. Затем по­вер­нул на север и прошёл 90 м. На каком рас­сто­я­нии (в метрах) от дома ока­зал­ся мальчик?

Задание 15 № 316352

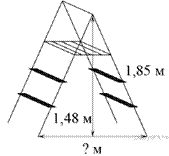Длина стре­мян­ки в сло­жен­ном виде равна 1,85 м, а её вы­со­та в раз­ло­жен­ном виде со­став­ля­ет 1,48 м. Най­ди­те рас­сто­я­ние (в метрах) между ос­но­ва­ни­я­ми стре­мян­ки в раз­ло­жен­ном виде.

Задание 15 № 316378

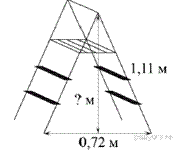Длина стре­мян­ки в сло­жен­ном виде равна 1,11 м, а рас­сто­я­ние между её ос­но­ва­ни­я­ми в раз­ло­жен­ном виде со­став­ля­ет 0,72 м. Най­ди­те вы­со­ту (в метрах) стре­мян­ки в раз­ло­жен­ном виде.

Задание 15 № 322886

Лест­ни­ца со­еди­ня­ет точки A и B и со­сто­ит из 20 сту­пе­ней. Вы­со­та каж­дой сту­пе­ни равна 16,5 см, а длина — 28 см. Най­ди­те рас­сто­я­ние между точ­ка­ми A и B(в мет­рах).

Задание 15 № 324941

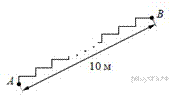
Лест­ни­ца со­еди­ня­ет точки A и B . Вы­со­та каж­дой сту­пе­ни равна 14 см, а длина — 48 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 10 м. Най­ди­те вы­со­ту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в мет­рах).

Задание 15 № 324946

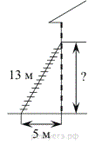
По­жар­ную лест­ни­цу дли­ной 13 м при­ста­ви­ли к окну пя­то­го этажа дома. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 5 м. На какой вы­со­те рас­по­ло­же­но окно? Ответ дайте в мет­рах

Задание 15 № 324948

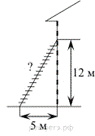
Пожарную лестницу приставили к окну, расположенному на высоте 12 м

от земли. Нижний конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.

Задание 15 № 325270

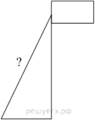
Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 5,5 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 4,8 м. Най­ди­те длину троса. Ответ дайте в мет­рах.

Задание 15 № 325275

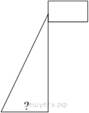
Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 6,3 м от земли. Длина троса равна 6,5 м. Най­ди­те рас­сто­я­ние от точки ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле. Ответ дайте в мет­рах.

Задание 15 № 325281

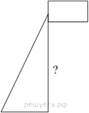
Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 1,6 м. Длина троса равна 3,4 м. Най­ди­те рас­сто­я­ние от земли до точки креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии. Ответ дайте в мет­рах.

Задание 15 № 333123

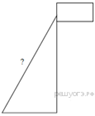Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном положении, на­хо­дит­ся на вы­со­те 6,3 м от земли. Рас­сто­я­ние от ос­но­ва­ния флагштока до места креп­ле­ния троса на земле равно 1,6 м. Най­ди­те длину троса в метрах.

Задание 15 № 333150

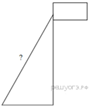Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном положении, на­хо­дит­ся на вы­со­те 4,4 м от земли. Рас­сто­я­ние от ос­но­ва­ния флагштока до места креп­ле­ния троса на земле равно 3,3 м. Най­ди­те длину троса в метрах.

Задание 15 № 341503

Лестница со­еди­ня­ет точки A и B. Вы­со­та каж­дой сту­пе­ни равна 10,5 см, а длина равна 36 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 7,5 м. Най­ди­те высоту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в метрах).

Задание 15 № 341529

Лестница со­еди­ня­ет точки A и B и со­сто­ит из 30 ступеней. Вы­со­та каж­дой сту­пе­ни равна 16 см, а длина равна 63 см. Най­ди­те рас­сто­я­ние между точ­ка­ми A и B (в метрах).

 

 

Квадрат

Задание 18 № 169862

Сторона квад­ра­та равна 10. Най­ди­те его площадь.

Задание 18 № 169863

Периметр квад­ра­та равен 40. Най­ди­те площадь квадрата.

Задание 18 № 322861

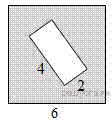
Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

Задание 18 № 323977

Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

Задание 18 № 323997

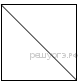Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

Задание 18 № 324364

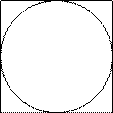Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 83.

Параллелограмм

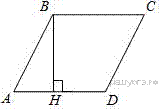
Задание 18 № 65

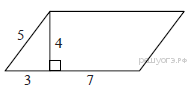Найдите пло­щадь параллелограмма, изображённого на рисунке.

Задание 18 № 169868

Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

Задание 18 № 169869

Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Задание 18 № 169872

Периметр ромба равен 24, а синус од­но­го из углов равен . Най­ди­те площадь ромба.

Задание 18 № 169875

Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

Задание 18 № 169876

Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на .

Задание 18 № 169878

Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен . Най­ди­те площадь параллелограмма.

Задание 18 № 169879

Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен . Най­ди­те площадь параллелограмма.

Задание 18 № 169880

Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен . Най­ди­те площадь параллелограмма.

Задание 18 № 169889

В пря­мо­уголь­ном треугольнике один из ка­те­тов равен 10, ост­рый угол, при­ле­жа­щий к нему, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те площадь треугольника, делённую на .

Задание 18 № 169900

В ромбе сто­ро­на равна 10, одна из диагоналей — , а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

Задание 18 № 169912

Радиус круга равен 3, а длина огра­ни­чи­ва­ю­щей его окруж­но­сти равна 6π. Най­ди­те площадь круга. В ответ за­пи­ши­те площадь, деленную на π.

Задание 18 № 314870

Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

Задание 18 № 323957

Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

Задание 18 № 324017

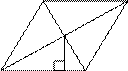Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

Задание 18 № 324097

Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

Задание 18 № 324117

Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Задание 18 № 339859

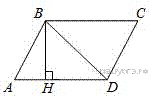
Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

Задание 18 № 340367

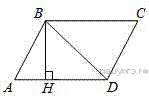
Высота BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 5 и HD = 8. Най­ди­те площадь ромба.

Задание 18 № 341330

Диагональ AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 30° и 45° . Най­ди­те боль­ший угол параллелограмма. Ответ дайте в градусах.

Задание 18 № 341523

Площадь ромба равна 54, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

Задание 18 № 348821

Высота ромба делит его сторону на отрезки и . Найдите площадь ромба.

Прямоугольный треугольник

Задание 18 № 169840

В пря­мо­уголь­ном треугольнике один из ка­те­тов равен 10, а угол, ле­жа­щий напротив него, равен 45°. Най­ди­те площадь треугольника.

Задание 18 № 323159

Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 28 и 100.

Задание 18 № 323356

В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

 

Прямоугольник

Задание 18 № 169864

В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сторона равна 12. Най­ди­те площадь прямоугольника.

Задание 18 № 169867

В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на .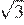

Задание 18 № 169898

В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны 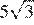. Най­ди­те площадь прямоугольника, деленную на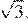

Задание 18 № 311761

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

Задание 18 № 311849

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

Задание 18 № 316321

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше другой.

Задание 18 № 324077

В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

Задание 18 № 340106

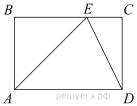
На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 12 и AD = 17, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.

Равнобедренный треугольник

Задание 18 № 169847

Сторона рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на .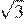

Задание 18 № 169848

Периметр рав­но­сто­рон­не­го треугольника равен 30. Най­ди­те его площадь, делённую на .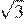

Задание 18 № 169849

Высота рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на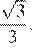

Задание 18 № 169850

В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, делённую на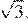

Задание 18 № 169851

Периметр рав­но­бед­рен­но­го треугольника равен 16, а бо­ко­вая сторона — 5. Най­ди­те площадь треугольника.

Задание 18 № 169893

В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, основание — 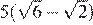, а угол, ле­жа­щий напротив основания, равен 30°. Най­ди­те площадь треугольника.

Задание 18 № 323179

Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Задание 18 № 323396

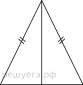Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.

Трапеция

Задание 18 № 39

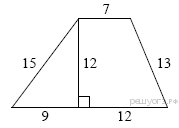Най­ди­те площадь трапеции, изображённой на рисунке.

Задание 18 № 117

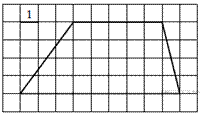Найдите пло­щадь трапеции, изображённой на рисунке.

Задание 18 № 143

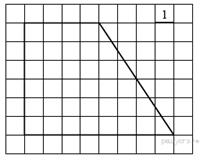Найдите пло­щадь трапеции, изображённой на рисунке.

Задание 18 № 169

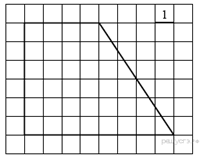Найдите пло­щадь трапеции, изображённой на рисунке.

Задание 18 № 169881

Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 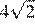, а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те площадь трапеции.

Задание 18 № 169883

Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен 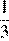. Най­ди­те площадь трапеции.

Задание 18 № 169884

Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен 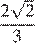. Най­ди­те площадь трапеции.

Задание 18 № 169885

Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а тан­генс угла между ней и одним из ос­но­ва­ний равен 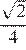. Най­ди­те площадь трапеции.

Задание 18 № 311480

Средняя линия тра­пе­ции равна 11, а мень­ше основание равно 5. Най­ди­те большее ос­но­ва­ние трапеции.

Задание 18 № 311682

Най­ди­те площадь трапеции, изображённой на рисунке.

Задание 18 № 314876

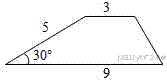
Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

Задание 18 № 314882

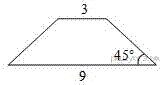
В рав­но­бед­рен­ной тра­пе­ции ос­но­ва­ния равны 3 и 9, а один из углов между бо­ко­вой сто­ро­ной и ос­но­ва­ни­ем равен 45°. Най­ди­те пло­щадь тра­пе­ции.

Задание 18 № 316347

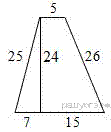
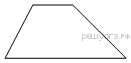
Найдите пло­щадь трапеции, изображённой на рисунке.

Задание 18 № 316373

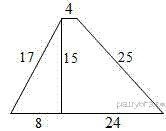
Найдите пло­щадь трапеции, изображённой на рисунке.

Задание 18 № 323902

Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 5 и 17, а ее бо­ко­вые сто­ро­ны равны 10. Най­ди­те пло­щадь тра­пе­ции.

Задание 18 № 324155

Ос­но­ва­ния тра­пе­ции равны 7 и 49, одна из бо­ко­вых сто­рон равна 18 , а ко­си­нус угла между ней и одним из ос­но­ва­ний равен 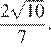Най­ди­те пло­щадь тра­пе­ции.

Задание 18 № 339837

Основания тра­пе­ции равны 1 и 13, одна из бо­ко­вых сто­рон равна 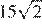, а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь трапеции.

Задание 18 № 340197

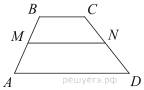
В тра­пе­ции ABCD AD = 5, BC = 2, а её пло­щадь равна 28. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 340408

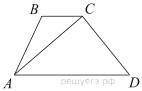
В тра­пе­ции ABCD AD = 3, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

Задание 18 № 341356

Тангенс остро­го угла пря­мо­уголь­ной тра­пе­ции равен 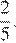Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 58.

Задание 18 № 341382

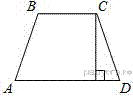
Высота рав­но­бед­рен­ной трапеции, проведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 2 и 9. Най­ди­те длину ос­но­ва­ния BC.

Задание 18 № 341497

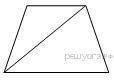
Основания рав­но­бед­рен­ной тра­пе­ции равны 4 и 14, бо­ко­вая сто­ро­на равна 13. Най­ди­те длину диа­го­на­ли трапеции.

Задание 18 № 348628

Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен 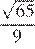. Найдите площадь трапеции.

Задание 18 № 349108

В тра­пе­ции ABCD известно, что AD = 6, BC = 2, а её пло­щадь равна 32. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349118

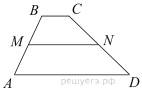
В тра­пе­ции ABCD известно, что AD = 5, BC = 1, а её пло­щадь равна 51. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349207

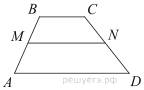
В тра­пе­ции ABCD известно, что AD = 8, BC = 5, а её пло­щадь равна 52. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349241

В тра­пе­ции ABCD известно, что AD = 2, BC = 1, а её пло­щадь равна 48. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349295

В тра­пе­ции ABCD известно, что AD = 7, BC = 5, а её пло­щадь равна 72. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349592

Основания тра­пе­ции равны 6 и 24, одна из бо­ко­вых сторон равна 11, а синус угла между ней и одним из ос­но­ва­ний равен 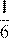. Най­ди­те площадь трапеции.

Задание 18 № 349659

В тра­пе­ции ABCD известно, что AD = 5, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 349665

Основания тра­пе­ции равны 7 и 63, одна из бо­ко­вых сторон равна 18, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен 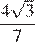. Най­ди­те площадь трапеции.

Задание 18 № 349714

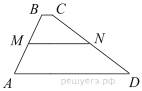
В тра­пе­ции ABCD известно, что AD = 9, BC = 1, а её пло­щадь равна 70. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

Задание 18 № 351297

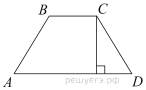
Высота равнобедренной трапеции, проведённая из вершины , отсекает от основания 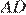отрезок длиной 2. Длина основания 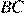равна 7. Найдите длину основания .

 

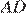ТРЕУГОЛЬНИК

Задание 18 № 169853

В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее высота — 5. Най­ди­те площадь треугольника.

Задание 18 № 169854

В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна 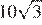, а угол между ними равен 60°. Най­ди­те площадь треугольника.

Задание 18 № 323436

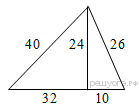Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

Задание 18 № 341524

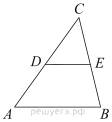
В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

Задание 18 № 349889

Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.