Теория релаксационной спектроскопии глубоких уровней.

Физические процессы DLTS изложены выше. Основное достижение DLTS схемы, представленной здесь, заключается в удобстве и быстроте, с которыми может быть получена информация, содержащаяся в экспериментах с последовательностью релаксаций емкости. То есть, информация, получаемая с помощью нескольких 10-ти минутных DLTS термических сканирований, может быть получена также путем более утомительного и с большей затратой времени измерения релаксации емкости по точкам при различных фиксированных температурах. Последняя процедура может быть полезна для детального исследования неизвестной ловушки, так как она более точна, однако, для первоначальной характеризации многих ловушек в неизвестном образце или в случае контролирующей работы большого объема DLTS – схема обладает очевидными преимуществами.

Существенной особенностью DLTS является возможность установить окно скорости эмиссии, при котором измерительная аппаратура дает отклик только в случае релаксации со скоростью эмиссии в пределах данного окна. Таким образом, если скорость эмиссии ловушки изменяется с изменением температуры образца, аппаратура покажет пик отклика при температуре, для которой скорость эмиссии находится в пределах окна. Скорости эмиссии имеют термически актив анионную зависимость, и, согласно принципу детального равновесия, могут быть записаны в виде:

e ₁ =(σ₁<ν₁> N_{D 1} /g₁ )exp(-Δ E /κ T )      (4)

где σ ₁ - сечение захвата неосновных носителей, < ν ₁ > - средняя тепловая скорость неоснов­ных носителей, N_{D 1} - эффективная плотность состояний в зоне неосновных носителей, g₁ -вырождение уровня ловушки и ΔЕ — энергетическое расстояние между уровнем ловушки и зоной неосновных носителей. Аналогичное уравнение справедливо для е₂ с изменением всех индексов равных 1 на 2 и всех величин на величины, относящиеся к основным носителям. Стандартный способ характеризации глубины ловушки заключается в построении графика зависимости loge ₁ или loge ₂ от 1000/T и получении из наклона результирующей прямой энергии активации ловушки. Эта величина равна ΔЕ, если только коэффициенты перед экспонентой в уравнении (4) не зависят от температуры. Поскольку эти коэффициенты, вообще говоря, зависят от температуры, необходимо это учитывать, чтобы получить точное значение ΔЕ.

На рис.5 приведен типичный график активационной зависимости, и показано, как измерительная система. дающая отклик на релаксацию в заданном окне скорости эмиссии, может разрешать сигналы от разных ловушек, зависящие от температуры. Существует сильная температурная зависимость скорости эмиссии согласно уравнению (4), которая позволяет путем температурного сканирования с данным окном скорости эмиссии разрешать сигналы.

Представленная здесь DLTS - схема использует накопитель сигналов (двойной бокскар) с двумя стробированиями (моментами времени измерений), что позволяет точно определить окно скорости эмиссии и обеспечить усреднение сигнала для улучшения отношения сигнал-шум. что необходимо для обнаружения ловушек с низкой концентрацией. В сочетании с быстродействующим измерителем релаксации емкости (детали в работе) максимальная достижимая скорость эмиссии примерно равна 10⁵ сек^-1. В принципе нет нижнего предела для скорости эмиссии. однако, практически нецелесообразно опускаться ниже 1 сек^-1 , так как время температурного сканирования становится довольно большим, при усреднении сигнала. Таким образом, можно охватить интервал по крайней мере в пять порядков величин скорости эмиссии.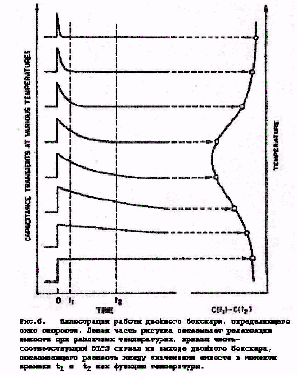

Использование двойного бокскара для выбора окна скорости эмиссии иллюстрируется на рис.6. Релаксация емкости наблюдается с помощью быстродействующего емкостного моста. Последовательность таких релаксаций емкости для типичной ловушки при различных температурах схематически показана в левой части рис.6. Согласно уравнению (4) и рис.5, скорость эмиссии очень мала для низких температур и становится более быстрой с ростом температуры. Этот пример приведен для ловушки неосновных носителей (ΔС >0 при t=0), которая заполнена в момент t=0 насыщающим импульсом инжекции. Реальный сигнал периодически повторяется на временной шкале, несколько превышающей показанную на рис.5. Сигналы релаксации поступают на двойной бокскар с установленными стробами t ₁ и t ₂ (рис.6), Сигнал дифференциального выхода бокскара поступает на вход Y двух - координатного самописца. Этот сигнал есть разность значений емкости в моменты времени t ₁ и t ₂. Из рис.6 видно, что величина С( t ₁ )-С( t ₂ ) проходит через максимум, когда τ величина обратная скорости эмиссии, становится приблизительно равной t ₁ и t ₂. Таким образом, величины t ₁ и t ₂. определяют окно скорости эмиссии при температурном сканировании DLTS сигнала.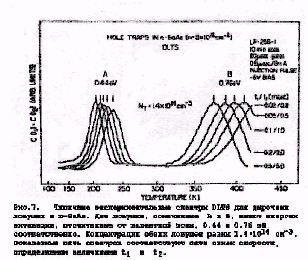

Теперь получим соотношение между τ_max (значением τ в максимуме С( t ₁ )-С( t ₂ )) при некотором значении T для данной ловушки и моментами измерений t ₁ и t ₂. Величину, которую будем называть не совсем точно окном скорости, определим как τ_max^-1. Для простоты получим желаемое выражение, считая временной интервал измерений бесконечно малым. Можно показать, однако, что результат справедлив также при менее строгом условии, когда временной интервал много меньше τ_max Полное решение для произвольного значения временных интервалов измерений получается непосредственно, но громоздко, и здесь не приводится. Представим нормированный сигнал DLTS, S ( T ) показанный в правой части рис.6 в виде

S ( T )=( С( t ₁ )-С( t ₂ ))/ ΔC (0)     (5)

где ΔС(0) - изменение емкости, обусловленное импульсом в момент t =0. Тогда для экспо­ненциальной релаксации имеем

S ( T )=( exp (- t ₁ / τ )- exp (- t ₂ / τ )),           (6)

где температурная зависимость τ дается уравнением (4). Можно также записать

S ( T )= exp (- t ₁ / τ )-(1- exp (- Δt / τ )),       (7)

где Δ t = t ₂ – t ₁ . Соотношение между τ_max и t₁ и t₂ просто определяется дифференцированием S (Т) относительно τ и приравниванием результата нулю. Искомое выражение имеет вид

τ_max=(t₁ – t₂) (ln(t₁/t₂))^-1                  (8)

Таким образом, скорость эмиссии, соответствующая максимуму пика ловушки, наблюдаемого при термическом сканировании, есть точно определенная величина, которая может быть использована вместе с значением температуры пика для построения в полулогарифмическом масштабе графика энергии активации, как на рис.5. То есть, в максимуме сигнала можно измерить температуру и вычислить τ_max из уравнения (8), чтобы получить одну точку на графике зависимости log(e₁) или log(e₂) от 1000/T. Другие точки могут быть аналогично получены при сканированиях с установкой других моментов стробирования, и, следовательно, других значений τ_max и положений пиков ловушки. Величина пика связана с ΔС(0) уравнениями (7) и (8), и концентрация ловушек может быть определена из уравнения{3).

Очевидно из выше сказанного, что скорость изменения температуры не играет роли при определении формы и положения пиков DLTS. Однако это утверждение справедливо в определенных границах. То есть, если датчик температуры измеряет истинную температуру диода, и, если постоянная времени бокскара достаточно мала и не искажает сигнал, тогда скорость и направление термического сканирования не воздействуют на сигнал. Это означает, что можно наблюдать спектр при охлаждении с одним окном скорости и при нагревании с другим окном скорости, и сделать грубую опенку различных энергий активации в одном температурном цикле. В действительности, воспроизводимость при сканировании вверх и вниз по температуре с одним и тем же окном скорости - хороший способ подтвердить, что измеряемая температура верна и форма сигнала не искажена электронной аппаратурой.

Режимы работы

Делая серию термических сканирований для определения энергий активации, необ­ходимо изменять t₁ и t₂, чтобы получить различные окна скорости для каждого сканирования согласно уравнению (8). Три схемы изменения этих параметров кажутся естественными: а именно, (i) t ₁ фиксировано, изменяется t ₂; (ii) t ₂ фиксировано, изменяется t ₁; (iii) t ₁ / t ₂ фиксировано, изменяются t ₁ и t ₂ Третий вариант кажется предпочтительным по причинам, которые ниже обсуждаются.

На рис.7 показана серия спектров, полученных с пятью различными окнами скорости. Две ловушки неосновных носителей в образце n - GаАs обозначены для удобства А и В. Отсчитанные от валентной зоны, энергии активации, определенные путем тщательных измерений релаксации емкости по точкам при фиксированных температурах, равны, соответственно. 0.44 и 0.76 эВ. Концентрация обеих ловушек равна 1.4 10¹⁴ см^-3 в не легированном образце с n=5·10¹⁵ см^-3 , выращенном методом жидкофазной эпитаксии. Изменение t₁ и t₂ на рис.7 соответствует приведенному выше варианту (iii). Отметим важную особенность: пики смещаются относительно жестко, не изменяя формы с изменением окна скорости. При использовании метода (i) пики изменяют существенно и величину и форму: низкотемпературная сторона смещается с изменением t ₂, тогда как высокотемпературная сторона почти не смещается. Метод (ii) дает прямо противоположный результат - смещается высокотемпературная сторона, как и ожидалось.

Уравнение (8), конечно, справедливо для всех 3-х случаев, и данные, полученные тремя способами, согласуются. Однако, определять местоположение пика проще и эстетически приятнее, используя схему (iii) с фиксированным отношением. Кроме того, получение результатов упрощается, так как ln(t₁/t₂) становится константой в уравнении (8).

Интересно сравнить данные зависимости «скорость от 1/Т», полученные из рис.7, и данные, полученные путем серии тщательных измерении при различных фиксированных температурах. Температуры, соответствующие максимумам ловушечных пиков, помечены на рис.7 стрелками. Соответствующие скорости эмиссии при этих температурах просто рассчитываются из t ₁ и t ₂ с помощью уравнения (8). Результирующие точки данных показаны на рис.8 с горизонтальной полоской ошибки, указывающей неопределенность локализации максимумов пиков на рис.7. Сплошная линия получена путем многих тщательных измерений релаксаций емкости при фиксированных температурах. Пунктирная линия - это экстраполяция в случае В, так как пик DLTS наблюдался в температурном интервале отличном от того, в котором проводились измерения данных в фиксированных точках. Согласие между двумя методами действительно замечательное, принимая во внимание огромную разницу во времени и усилиях. необходимых для получения данных. В качестве демонстрации точности DLTS метода, подчеркнем снова — то, что сделано на рис.8, это только определение положений максимумов пиков на рис,7 в сочетании с уравнением (8) и установкой моментов времени измерений. Без использования каких-либо регулируемых параметров получено очень хорошее согласие с чрезвычайно точным результатом.

Также легко получить концентрацию ловушек из температурного DLTS сканирования. Так как τ_max определяется установкой величин t ₁ и t ₂, можно, используя уравнения (6) и (7) в сочетании с (5). получить -ΔС(О) для максимума пика. Затем. если импульс основных носителей достаточно большой и достаточно длительный, чтобы полностью заполнить ловушки, можно использовать (3) для расчета концентрации ловушек. Последнее условие легко контролировать, сделав несколько сканирований с возрастающими по величине и длительности импульсами, пока пик ловушки не будет больше расти. Контроль концентраций ловушек с известными свойствами на серии образцов становится особенно удобным с помощью DLTS метода. А priori известно, где на температурной шкале будет появляться данная ловушка для определенного окна скорости, известны также величина и длительность импульса инжекции, необходимые для полного заполнения ловушки, что позволяет применять уравнение (3). Достаточно сканирования с понижением температуры и медленным окном скорости и последующего сканирования с повышением температуры, чтобы сделать видимыми большинство типов ловушек в регулируемом температурном интервале. Следует указать, однако, что описанная выше схема строго справедлива только в случае ловушек с экспоненциальной релаксацией. Не экспоненциальный случай может иметь место, особенно для промежуточных и мелких ловушек, и должна быть соблюдена осторожность при анализе такой ситуации. Относительное сравнение од­ной и той же ловушки на серии образцов с одинаковым окном скорости все же справедливо. Единственная проблема в том, что нельзя использовать уравнения (5)-(8), чтобы определить ΔС(0) в не экспоненциальном случае, и абсолютное определение N с помощью (3) является более трудным.

Обсудим теперь более сложные измерения профилей концентрации и скоростей захвата. Процедура такая же, как на рис.7, за исключением того, что все ловушки измеряются вместе при температурном сканировании, при этом нет трудностей разделения сигналов, которые существуют в методе фиксированных температур. Изложим здесь способ кратко, для более полного обсуждения читатель отсылается к работе.

Профилирование концентрации и ловушек при DLTS сканировании является непосредственным, однако, требует некоторого числа сканирования для достижения хорошего разрешения. Рис. 9 и 10 показывают типичные данные о концентрационном профиле ловушек неосновных носителей А и В в n - GaAs. Сущность метода та же, что и при фиксированных температурах в работе, а именно, в наблюдении зависимости величины сигнала от напряжения импульса основных носителей. Для ловушек основных носителей это особенно просто: если изменять импульс основных носителей от нуля до максимальной величины, то сразу после инжекции пики ловушек возрастают соответственно большей доле равновесной области обеднения, в которой ловушки заполнены (рис.3). При этом необходимо использовать достаточно длительный импульс, чтобы полностью заполнить исследуемые ловушки основными носителями в области, определяемой амплитудой импульса. Затем строится график зависимости сигнала от напряжения импульса основных носителей, аналогичный изображенном на рис.10. Если это прямая линия, то, как показано ранее, профиль концентрации ловушек пропорционален профилю носителей. Отклонение от линейности указывает на соответствующее отклонение от профиля носителей.

Для профилирования ловушек неосновных носителей требуется два импульсных генератора (рис.9 и 10). Первый импульс, как при обычном DLTS сканировании, - насыщающий импульс инжекции, который заполняет все ловушки неосновными носителями в исследуемой области (рис.2). Второй импульс, как в работе, это импульс основных носителей, регулируемого напряжения и длительности достаточной, чтобы полностью опустошить ловушки от неосновных носителей в области, определяемой напряжением импульса. Как и в случае ловушек основных носителей, делают серию сканирований, постепенно увеличивая импульс основных носителей (рис.9), но при этом строят график зависимости убывания сигнала от напряжения импульса (рис.10), чтобы определить профиль. Используя уравнение (А7) из работы, данные рис.10 и профиль носителей в данном образце, мы определили, что обе ловушки (А и В) имеют однородное распределение и концентрацию около 1,4 · 10¹⁴ см^-3 .

Скорость захвата определена путем измерения высоты пика как функции инжекции, или ширины импульса основных носителей, как в работе. Рис.11 показывает типичный пример для случая радиационного дефекта-ловушки в n - GaAs. Отметим также, что разница знаков для ловушек основных и неосновных носителей иллюстрируется графически. Чтобы измерить обе скорости захвата для данной ловушки, необходимо использовать два генератора импульсов - один для измерения скорости заполнения, второй - для измерения скорости опустошения, когда ловушка заполнена. Скорость захвата основных носителей измеряется непосредственно. Для этого просто строится график высоты сигнала в 'зависимости от ширины импульса основных носителей. Захват неосновных носителей более сложен, так как скорость его зависит от концентрации инжектированных неосновных носителей. Построив скорость заполнения для ловушки неосновных носителей или скорость опустошения для ловушки основных носителей как функцию тока инжекции можно получить скорость захвата неосновных носителей. Абсолютные значения трудно получить для GaAs из-за сложности в установлении соотношения между концентрацией неосновных носителей и измеряемым током импульса инжекции. Однако, эта проблема менее строгая в Si и GaP.

Пожалуй, большинство важных ловушек действуют как центры быстрой безизлучательной рекомбинации. Так как такие ловушки определяют рекомбинирующую кинетику, их присутствие желательно, например, в быстрых полупроводниковых переключателях, но вредно для работы полупроводниковых лазеров и излучающих световых диодов. DLTS метод обеспечивает особенно простой способ изменить спектр в пользу таких ловушек быстрого захвата, в тоже время подавляя сигнал от более медленных ловушек, а именно, использовать очень короткие импульсы, как показано на рис.11. Такие короткие импульсы могут заполнить быстрые ловушки, но не могут существенно заполнить медленные ловушки. Таким образом, ширина импульса является эффективным дискриминатором в методе DLTS, позволяя подавлять сигналы от медленных и. возможно, менее интересных ловушек.

В заключение, скажем несколько слов о проблеме не экспоненциальных релаксаций, упомянутой выше. Еще раз подчеркнем, что весь изложенный анализ строго справедлив только для экспоненциальных релаксаций емкости. DLTS метод все же хорошо работает в случае неэкспоненциальных релаксаций, однако, нужно соблюдать осторожность, определяя абсолютные значения параметров ловушки из экспериментальных данных. Тем не менее, относительное сравнение от образца к образцу с одним и тем же окном скорости вполне применимо независимо о формы релаксации.

Не экспоненциальное поведение из-за пространственного варьирования скорости эмиссии ловушки, обусловленное пространственным изменением электрического поля р-п перехода, относительно легко обнаружить методом DLTS. Такое поведение типично для ZnO центра в GaP. Пример пространственно неоднородной скорости эмиссии, обнаруженной с помощью DLTS, показан на рис.12 для радиационно введенных ловушек в n - GaAs. Чтобы наблюдать неоднородность такого типа, нужно следовать процедуре профилирования концентрации. описанной выше. Если, как на рис.12. положение и форма пика меняются с изменением напряжения импульса, значит имеется пространственная неоднородность. Это можно понять, рассматривая область обеднения как разделенную на n частей, в каждой из которых сигнал является чисто экспоненциальным, но с разными константами скорости в каждой части. Каждый из этих n-сигналов появляется в разных положениях при DLTS сканировании. Когда все они присутствуют вместе, наблюдается широкий пик ловушки, в котором индивидуальные компоненты не разрешаются. При меньшем числе этих сигналов, как это делается в последовательности измерения концентрационных профилей, широкий пик сдвигается и сужается по мере удаления некоторых компонент линии. Пик однородной ловушки в силу чисто экспоненциальной релаксации будет оставаться фиксированным по положению и по форме (рис.9).