Адаптивные регуляризирующие алгоритмы

1. Пусть Z,U – гильбертовы пространства, а A – линейный ограниченный оператор, действующий из Z в U. Рассмотрим операторное уравнение

 

 

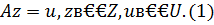
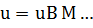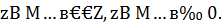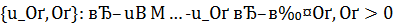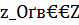Без ущерба для общности будем считать, что ||A||<1. Предположим, что для  уравнение (1) имеет нормальное псевдорешение  . Будем решать задачу его устойчивого нахождения по приближенным данным уравнения (1)  , пологая оператор А заданным точно. Таким образом, требуется по данным  найти такой элемент ,который сильно сходиться в Z к  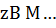при  .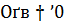

2. Эта задача может быть решена многими методами (регуляризирующими алгоритмами). Например, для ее решения можно использовать метод невязки (в обобщенной форме для решения несовместных уравнений). В этом методе приближение 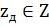 к 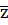 ищется как решение экстремальной задачи

 

.

 

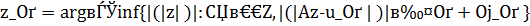Здесь 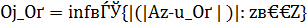 - оценка меры несовместности

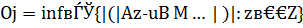 решаемого операторного уравнения. Известно, что без привлечения дополнительной информации об искомом решении  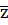или о точных данных задачи ( 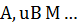) метод невязки не может обеспечить точность приближенного решения лучше, чем 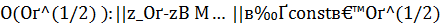. Аналогичная ситуация складывается и при использовании метода регуляризации А. Н. Тихонова, в котором наилучшая возможная точность есть 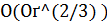, как бы ни выбирался параметр регуляризации. Это явление обычно называют «насыщением точности» регуляризирующего алгоритма (РА). Его можно избежать, если учесть в РА априорную информацию о свойствах точного решения. Например, если известно, что 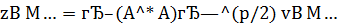, где 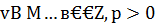, то, используя величину p, можно построить РА, которые дают приближение с порядком точности 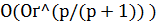, оптимальным на классе задач (1) с решениями указанного вида.

С другой стороны, можно, не зная величины р, но используя оценку 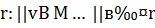, построить РА, которые позволяют устойчиво определять число р и получать приближение к  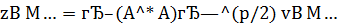с оптимальным порядком точности для произвольного р>0. Алгоритмы такого рода предлагаются в данной заметке.

3. Сформулируем основные положения. Пусть известно, что нормальное псевдорешение 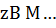 задачи (1) истокообразно представимо с помощью степени оператора 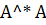. Поскольку такое представление не единственно, будем иметь ввиду, что

 

 

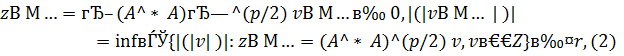
где р>0 – максимально возможное число. В общем случае число р полагается неизвестным, но при этом считается, что дана величина r.

Ниже будет использована величина  - устойчивая оценка меры несовместимости 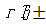 уравнения (1), удовлетворяющая требованиям: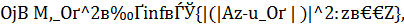  

 

.

 

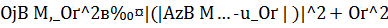В качестве 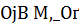 можно выбрать, например, упомянутое выше число .

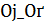4. Методику построения алгоритмов рассмотрим на примере специализированного метода невязки. Предлагаемый РА основан на решении экстремальной задачи: при заданном параметре 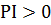 найти элемент  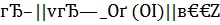такой, что

 

 

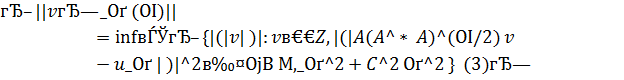
(C=const > 1). Алгоритм состоит из двух шагов:

1) Найти число

 

 

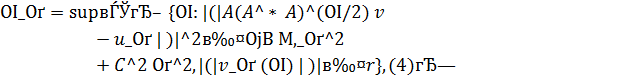
2) Вычислить при 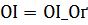 решение  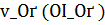задачи (3) и применять элемент  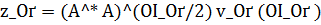в качестве приближения к .

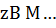Экстремальные задачи (3), (4) обладают важными свойствами.

Теорема 1. Пусть выполнено (2). Тогда задача (3) однозначно разрешима при всяком 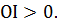 Для каждого 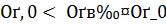, найдется такое число 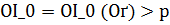, что при любом 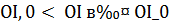, для решения задачи (3) справедлива оценка: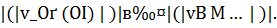

Теорема 2. Если выполнено (2), то решение задачи (4) конечно, и при каждом 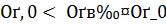, для него верна оценка

 

.

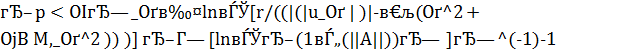Теорема 3. Если 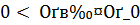, то для решения  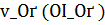задачи (3) при  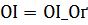выполнено неравенство .

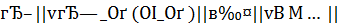Сходимость приближенных решений устанавливает

Теорема 4. Если выполнено условие (2), то 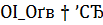 при 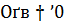 и обеспечены сильные сходимости в Z:

 

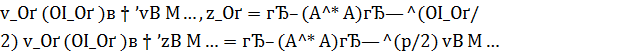. При этом .

 

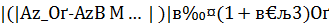Введем множество 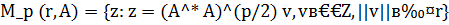. Ясно, что 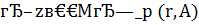. Тогда из приведенной в теореме 4 оценки и из теории оценивания погрешности приближенных решений некорректных задач на множествах типа  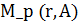вытекает

Теорема 5. При выполнении условий (2) метод (3), (4) гарантирует при любом р>0 оптимальный порядок точности приближенного решения для задач (1), у которых .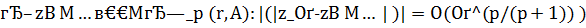

Рассмотрим случай, когда оператор А – вполне непрерывный. Тогда множество 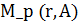 - образ слабого компакта в Z – является сильным компактом. Это следует из того, что оператор  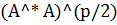также будет вполне непрерывным. По этой причине задача решения уравнения (1) приобретает интересные свойства. На основе этих свойств могут быть построены регуляризирующие алгоритмы, допускающие апостериорную оценку погрешности решения.

Отметим теперь следующий тривиальный результат.

Теорема 6. Если в дополнение к условиям теоремы 5 известны, что оператор А нормально разрешим, то алгоритм (3), (4) при любом р > 0 дает точность .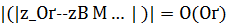

5. Из теорем 5,6 следует, что алгоритм (3), (4), не используя данных о степени р истокообразной представимости элемента 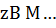, в процессе решения задачи сам «настраивается» на нужную величину р. В связи с этим дадим

Определение. Регуляризирующий алгоритм называется адаптивным для задач (1) с решениями из некоторого семейства множеств { 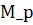}, зависящих от параметра р, если: 1) он не использует явно величину р, определяемую включением 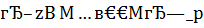; 2) он оптимален по порядку точности для всякого  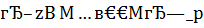независимо от допустимого параметра р.

Примером адаптивного РА служит алгоритм (3), (4). Имеются и другие адаптивные РА, для которых справедливы такие же результаты, как в теоремах 4-6. К числу таких РА относятся специализированный метод регуляризации А.Н. Тихонова, эквивалентный методу (3), (4), специализированный метод квазирешений, получаемый из обычного метода квазирешений [5] по схеме, которая использована в методе (3), (4). Все эти адаптивные алгоритмы были программно реализованы в системе MATLAB и показали свою высокую эффективность в численных эксперементах.

6. Остановимся особо на случае, когда при выполнении условий (2) степень истокопредсавимости р точного решения задачи (1) известна. Тогда нет необходимости использовать величину r. В качестве приближения к 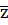 в этом случае можно взять элемент  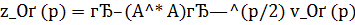- решение задачи (3) при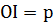

Справедлива

Теорема 7. Гарантированы сильные сходимости: 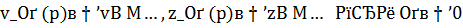. Приближение  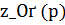имеет оптимальный порядок точности 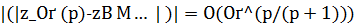. Если оператор А нормально разрешим, то при всяком р > 0 верна оценка: 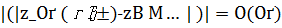. (Ист. №7)

Кроме специализированного метода невязки, адаптивными являются также и некоторые другие регуляризующие алгоритмы. Сформулируем и кратко обсудим важнейшие из них.

Специализированный метод регуляризации А. Н. Тихонова. Он основан на решении следующей параметрической задачи: при фиксированном β > 0 и при заданном параметре α>0 найти элемент 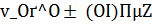, такой что

 

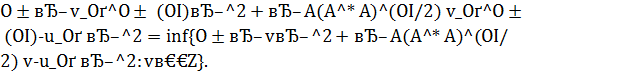(5.1)

 

Алгоритм этого метода состоит из таких шагов: 1) выбор параметра регуляризации α(δ,β)>0 для каждого β > 0 по (обобщенному) принципу невязки , то есть как решение уравнения

 

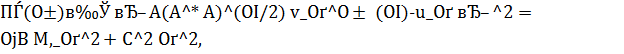(5.2)

 

2)использование элементов 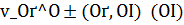, получаемых в результате решения задачи (5.1) с

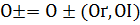, для нахождения числа  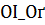по правилу

 

 

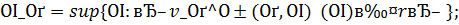
3) принятие в качестве приближения к 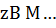 элемента  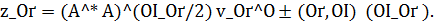Имеется тесная связь метода регуляризации с выбором параметра регуляризациипо (обобщенному) принципу невязки и метода невязки.

Теорема 8.Элемент 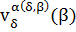, вычисляемый в шагах 1, 2 алгоритма специализированного метода регуляризации, по крайней мере при достаточно малых δ совпадает с элементом  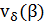, полученным в специализированном методе невязки. Число 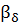, определяемое этими алгоритмами, — одно и то же при таких δ.

Доказательство . Существование единственного решения задачи (5.1) следует из общей теории метода регуляризации линейных некорректных задач в гильбертовых пространствах. Существование и единственность параметра регуляризации 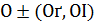, выбираемого из условия (5.2), при каждом фиксированном βвытекает из результатов работ. Установлена эквивалентность принципа и метода невязки при решении линейных операторных уравнений в гильбертовых пространствах в случае, если  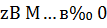и δ достаточно мало. Поэтому  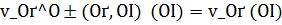при каждом  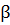> 0. Но тогда задача нахождения величины  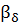оказывается одной и той же для обоих специализированных алгоритмов и поэтому имеет одно и то же решение.

В силу установленной в теореме 4.1 эквивалентности алгоритмов специализированного метода регуляризации и специализированного метода невязки для первого из них справедливы те же результаты о сходимости и оптимальности порядка точности приближений, что и для второго. Это можно суммировать так.

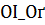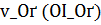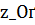Теорема 9.Пусть выполнены условия (2). Тогда для величин ,  и , полученных по специализированному методу регуляризации, гарантируются сходимости при .

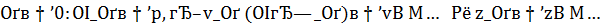Этот метод оптимален по порядку точности при всяких 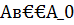 и при каждом p > 0. Он обеспечивает неулучшаемый порядок точности на всем классе 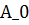, каково бы ни было p > 0, причем гарантированная верхняя оценка точности есть  .

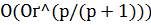Теорема 9 обосновывает адаптивность алгоритма специализированного метода регуляризации.

Специализированный метод квазирешений. Он базируется на решении экстремальной задачи: при фиксированном числе β > 0 найти элемент 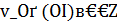 , для которого

 

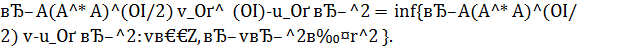(6.1)

 

В задаче (6.1) минимизируется непрерывный выпуклый (квадратичный) функционал на замкнутом, выпуклом, ограниченном множестве гильбертова пространства. Известно, что такая задача разрешима. Будем использовать далее произвольное ее решение 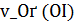 при каждом рассматриваемом β > 0. Алгоритм специализированного метода квазирешений состоит из следующих шагов: 1) найти число

 

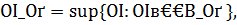                                          (6.2)

 

здесь числовое множество 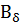 определяется так:

 

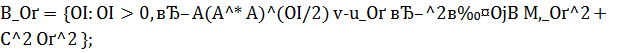(6.3)

 

2) решить при 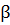 =  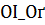задачу (6.1) и по ее решению  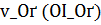найти приближение

.

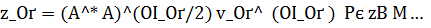 Множество 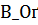 из задачи (6.2) не пусто по крайней мере для «малых δ»: 0 < δ <  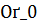Действительно при 0 < δ <  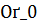и при 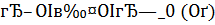 справедливо включение 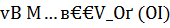. Из него и из задачи (6.1) с учетомоценки || 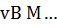||  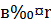для таких δ и βполучим:

 

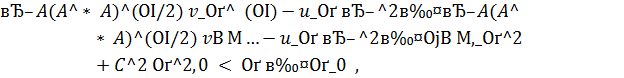
и это значит, что .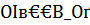

Конечность величины 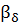 устанавливается, причем для этого  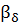верна та же оценка, что и в замечании 2. Из (6.1)-(6.3) следуют неравенства

 

 

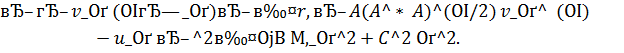
Используя их можно получить сходимост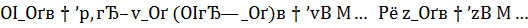и  при 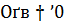. Из сказанного ясно, что для приближенных решений задачи (1), которые находятся по специализированному методу квазирешений, верны результаты теоремы 9. Поэтому данный алгоритм является адаптивным. (Ист.№8)

 

Вывод

 

Решение – это выбор альтернативы. Принятие решений – связующий процесс, необходимый для выполнения любой управленческой функции. Лицо,принимающее решение своими решениями может повлиять на судьбы многих людей и организаций. В зависимости от уровня сложности задач, среда принятия решений варьируется в зависимости от степени риска. Условия определенности существуют, когда руководитель точно знает результат, который будет иметь каждый выбор. Методы приближённого решения некорректно поставленных задач и их применений к решению обратных задач имеют важное значение для автоматизации обработки наблюдений и для решения проблем управления. Имеется много работ (особенно советских математиков), посвященные этим методам.

Существовало мнение, что некорректные задачи не могут встречаться при решении физических и технических задач и что для некорректных задач невозможно построение приближённого решения в случае отсутствия устойчивости. Расширение средств автоматизации при получении экспериментальных данных привело к большому увеличению объёма таких данных; необходимость установления по ним информации о естественнонаучных объектах потребовала рассмотрения некорректных задач. Развитие электронной вычислительной техники и применение её к решению математических задач изменило точку зрения на возможность построения приближённых решений некорректно поставленных задач.

Из определения регуляризирующего алгоритма легко следует, что, если есть хотя бы один регуляризирующий алгоритм, то их может быть сколько угодно. Выбрать же тот, который дает наименьшую ошибку, или сравнивать алгоритмы, сравнивая ошибки полученных приближенных решений, при решении некорректных задач, невозможно при отсутствии априорной информации, которая фактически преобразует такие задачи в корректные.

К числу адаптивных регуляризирующих алгоритмов относятся специализированный метод регуляризации А.Н. Тихонова, специализированный метод квазирешений, получаемый из обычного метода квазирешений по определенной схеме. Все эти адаптивные алгоритмы были программно реализованы в системе MATLAB и показали свою высокую эффективность в численных эксперементах.