Метод верхних релаксаций

линейный уравнение итерационный релаксация

Среди явных одношаговых итерационных методов наибольшее распространение получил метод верхних релаксаций (1.21). Это связано с тем, что метод верхних релаксаций содержит свободный параметр w, изменяя который можно получать различную скорость сходимости итерационного процесса.

Наиболее эффективно этот метод применяется при решении множества близких алгебраических систем линейных уравнений. На первом этапе проводится решение одной из систем с различными значениями итерационного параметра w и из анализа скорости сходимости итерационного процесса выбирается оптимальное значение этого параметра. Затем все остальные системы решаются с выбранным значением w.

Еще одно достоинство итерационного метода верхних релаксаций состоит в том, что при его реализации на ЭВМ алгоритм вычислений имеет простой вид и позволяет использовать всего один массив для неизвестного вектора.

Основная вычислительная формула имеет вид

 

(1.44)

 

В выражение (1.44) 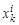 и  входят одинаковым образом, следовательно, при вычислениях они могут записываться в один и тот же массив. При реализации метода верхних релаксаций используется следующая форма записи алгоритма вычислений

 

.

(1.45)

 

Действительно, при последовательном нахождении элемента ( i+1 итерации) на каждом шаге будут использоваться найденные ранее значения, которые при k<j соответствуют i +1 итерации, а при k > j - i итерации.

Современная вычислительная техника позволяет проводить исследование устойчивости и сходимости итерационного метода в зависимости от параметров задачи. Например, можно проводить исследование влияния повышения точности решения задачи на число необходимых итераций, исследование влияния начального приближения, изменения коэффициентов матрицы А и правых частей системы.

 

1.2 Âû÷èñëèòåëüíûå ïîãðåøíîñòè ìåòîäà âåðõíèõ ðåëàêñàöèé

 

Один из основных вопросов применения итерационных методов связан с корректностью выбора точности метода e.

Àíàëèçèðóÿ âû÷èñëèòåëüíûå ïîãðåøíîñòè âûðàæåíèÿ (1.45), ïîëó÷èì îöåíêó íàèìåíüøåãî çíà÷åíèÿ òî÷íîñòè ìåòîäà âåðõíèõ ðåëàêñàöèé.

Очевидно, что искомая погрешность вычислений будет определяться погрешностью задания коэффициентов исходной системы и погрешностью округления.

Çàïèøåì ðàçíîñòü äâóõ èòåðàöèîííûõ ïðèáëèæåíèé ðåøåíèÿ è îöåíèì å¸ ìèíèìàëüíîå çíà÷åíèå

 

(1.46)

 

Пусть коэффициенты  и f_i заданы с некоторой относительной погрешностью . Предположим, что итерационный метод сходится, и невязка

 

(1.47)

 

бывает с ростом номера итерации k, т.е. . Оценка абсолютной погрешности правой части выражения (10) может быть представлена в следующем виде

 

,

(1.48)

 

здесь 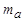.- модуль минимального значения диагонального элемента .Отсюда следует, что задаваемая погрешность метода .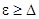

1.3 Ìåòîä áëî÷íîé ðåëàêñàöèè

 

Èñõîäíàÿ ìàòðèöà 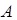 ðàçáèâàåòñÿ íà áëîêè (â ðàìêàõ ëàáîðàòîðíîé ðàáîòû áóäåì ðàññìàòðèâàòü ñëó÷àé, êîãäà  ðàçáèâàåòñÿ íà êâàäðàòíûå áëîêè ðàâíîé ðàçìåðíîñòè). Âåêòîð ïðàâîé ÷àñòè è âåêòîð íåèçâåñòíûõ ðàçáèâàþòñÿ íà áëîê-âåêòîðû ñîîòâåòñòâóþùåé ðàçìåðíîñòè. Íàïðèìåð, äëÿ ðàçìåðà áëîêà ðàâíîãî äâóì, ïîëó÷àåì:

 

(1.49)

 

ãäå

 

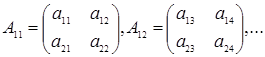
	(1.50)
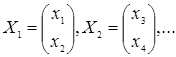
	(1.51)
	(1.52)

 

Çàïèøåì ôîðìóëó äëÿ áëîêîâ ìàòðèöû 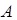 è áëîê-âåêòîðîâ  è :

 

(1.53)

 

Îáîçíà÷èì

 

	(1.54)
	(1.55)

 

Òîãäà, ïîäñòàâëÿÿ (1.54) è (1.55) â (1.53) è óìíîæàÿ ñëåâà íà , äëÿ êàæäîãî áëîê-âåêòîðà  ïîëó÷àåì ÑËÀÓ:

 

(1.56)

 

Ðåøåíèå ïîëó÷åííûõ ñèñòåì (1.56) ðåêîìåíäóåòñÿ âûïîëíÿòü ñ èñïîëüçîâàíèåì ôàêòîðèçàöèè ìàòðèöû , ïðè÷¸ì ôàêòîðèçàöèþ ñëåäóåò âûïîëíÿòü 1 ðàç ïåðåä ïåðâîé èòåðàöèåé.

2. ÐÀÇÁÎÐ ÌÅÒÎÄÀ ÐÅËÀÊÑÀÖÈÉ Â ÑÈÑÒÅÌÀÕ ËÈÍÅÉÍÛÕ ÓÐÀÂÍÅÍÈÉ ÍÀ ÏÐÈÌÅÐÅ

 

ПРИМЕР: решить методом релаксаций данную систему

 

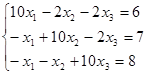
(2.1)

 

Вычисления производить с точностью до двух знаков после запятой.

РЕШЕНИЕ: Приводим систему(4) к виду, удобному для решения методом релаксации

 

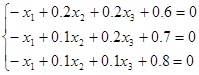
(2.2)

 

Задаем начальные приближения корней нулевыми значениями

 

(2.3)

 

Находим значения невязок

 

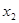
	0	0,60	0	0,70	0	0,80
		0,16		0,16		-0,80
		0,76		0,86		0
		0,17	0,86	-0,86		0,09
		0,93		0		0,09
	0,93	-0,93		0,09		0,09
		0		0,09	0,18	0,18
		0,04		0,04		-0,18
		0,04	0,13	0,13		0
		0,03		-0,13		0,01
	0,07	0,07		0		0,01
		-0,07		0,01		0,01
		0		0,01	0,02	0,02
		0		0		-0,02
		0
		0	0,01	0,01		0
		0		-0,01		0
		0		0		0
	1,00		1,00		1,00

 

Далее, решаем

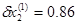
И так далее. Подставляем результаты вычисленные в таблице. Подсчитав все приращения , содержащее значение корней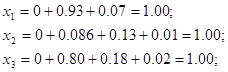

Для проверки подставляем найденные значения корней в исходное уравнение; в целом система решена точно.

Рисунок 1 – Решение системы с помощью языка Borland C++

 

Листинг программы решающий систему методом релаксаций переменных приведен в приложении.

ЗАКЛЮЧЕНИЕ

Можно утверждать, что почти любая задача вычислительной математики сводится в конечном итоге к решению полученной некоторым образом системы линейных или тензорных алгебраических уравнений (СЛАУ).

Но такие системы уравнений могут быть, во-первых, очень большого размера, например, NxN=10000х10000, и даже более; во-вторых, система уравнений может оказаться недоопределенной; в-третьих, она может оказаться с линейно зависимыми уравнениями; в-четвертых, она может оказаться переопределённой и несовместной. Кроме того, в-пятых, вычислительная техника может иметь далеко не рекордное быстродействие и объём оперативной памяти, и заведомо конечную разрядность двоичного представления чисел и связанные с этим ненулевые вычислительные погрешности. Поэтому итерационные методы получили большое применение в решении СЛАУ. Современная вычислительная техника позволяет проводить исследование устойчивости и сходимости итерационного метода в зависимости от параметров задачи.

Наиболее эффективно метод релаксаций применяется при решении множества близких алгебраических систем линейных уравнений. На первом этапе проводится решение одной из систем с различными значениями итерационного параметра w и из анализа скорости сходимости итерационного процесса выбирается оптимальное значение этого параметра. Затем все остальные системы решаются с выбранным значением w.

Еще одно достоинство итерационного метода верхних релаксаций состоит в том, что при его реализации на ЭВМ алгоритм вычислений имеет простой вид и позволяет использовать всего один массив для неизвестного вектора.

Я научился решать систем линейных уравнений методом релаксации(ослабления) переменных, и закрепил приобретённые навыки разработкой программы на языке Borland C++ 4.5.

СПИСОК ЛИТЕРАТУРЫ

 

1. Воеводин В.В. «Вычислительные основы линейной алгебры». Москва «Наука», 1977.

2. Фаддеев Д.К., Фаддеева В.Н. «Вычислительные методы линейной алгебры». Москва «Физматгиз», 1963.

3. Самарский А.А., Гулин А.В.» Численные методы». Москва «Наука», 1989.

4. Самарский А.А., Николаев Е.С. «Методы решения сеточных уравнений». Москва «Наука», 1978.

5. Самарский А.А. «Введение в численные методы». Москва «Наука», 1987.

6. Стренг Г. «Линейная алгебра и ее применение». Москва «Мир», 1980.

7. Карманов В.Г. «Математическое программирование». Москва «Наука», 1989.

8. Алексеев Е.Р. «Программирование на С++». Москва «НТ Пресс», 2007.

9. http://www.exponenta.ru/ - сайт посвящен решению математических задач в прикладных программных пакетах.

10. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: Наука, 1987.- 600 с.

ПРИЛОЖЕНИЕ

 

Листинг программы

#include<iostream.h>

#include<math.h>

int maximal(int n,double R0[]);

void main(){

int i,j,n,f,k,iter;

double S,det;

cout<<"Введите размерность матрицы(матрица должна быть квадратной)= ";cin>>n;

double *x=new double [n];

double **b=new double *[n];

for(i=0;i<n;i++)

 b[i]=new double[n+1];

double **a=new double *[n];

for(i=0;i<n;i++)

 a[i]=new double[n+1];

cout<<"Введите количество итераций:";

cin>>iter;

cout<<"Введите расширенную матрицу:\n";

for(i=0;i<n;i++){

for(j=0;j<=n;j++)

cin>>b[i][j];

}

cout<<"Подготавливаю матрицу к релаксации...\n";

for(i=0;i<n;i++){

for(j=0;j<n;j++)

a[i][j]=-b[i][j]/b[i][i];

a[i][n]=b[i][n]/b[i][i];

}

for(i=0;i<n;i++){

for(j=0;j<n+1;j++)

cout<<" "<<a[i][j]<<" || ";

cout<<"\n";

}

double *x0=new double [n];

for(i=0;i<n;i++)

x[i]=0.0;

double *R0=new double [n];

cout<<"Введите значения начальных приближений:\n";

for(i=0;i<n;i++)

cin>>x0[i];

S=0.0;

for(i=0;i<n;i++){

for(j=0;j<n;j++)

S=S+a[i][j]*x0[i];

}

for(i=0;i<n;i++){

R0[i]=a[i][n]-x0[i]+S;

cout<<"R("<<i<<")="<<R0[i]<<" | ";

}

f=maximal(n,R0);

det=R0[f];

for(k=0;k<iter;k++){

cout<<"det{"<<k<<"}="<<det<<"\n";

for(i=0;i<n;i++){

if(i!=f) R0[i]=R0[i]+a[i][f]*det;

else R0[i]=R0[i]-det;

}

for(i=0;i<n;i++)

cout<<"R["<<i+1<<"]="<<R0[i]<<" ";

x[f]=x[f]+det;

f=maximal(n,R0);

det=R0[f];

}

cout<<"\n";

for(i=0;i<n;i++)

cout<<"X{"<<i+1<<"}="<<x[i]<<"\n";

delete []x;

delete []R0;

delete []x0;

delete []a;

}

int maximal(int n, double R0[]){

int i,f;

f=0.0;

for(i=0;i<n-1;i++){

if(R0[i+1]>R0[i]) f=i+1;

}

return f;

}