ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ В ПЕРЕМЕННЫХ ПРОСТРАНСТВА СОСТОЯНИЙ

 

ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

 

Математическая модель системы в переменных пространства состояний имеет вид

,      (2.1.1)

                       (2.1.2)

где мерный вектор параметров состояний;  мерный вектор управляющих воздействий;  мерный вектор возмущающих воздействий; l- мерный вектор выходов; А – матрица состояний системы размерности ; В – матрица управлений размерности ; Г – матрица возмущений размерности ; С – матрица выходов размерности l n; D – матрица компенсаций (обходов) размерности l m.

Решение векторного дифференциального уравнения (2.1.1) имеет следующий вид:

, (2.1.3)

где  - экспоненциал матрицы А.

Подставляя выражение (2.1.3) в формулу (2.1.2), получаем интегральное уравнение движения системы в переменных «вход – выход».

Рассмотрение движения системы в переменных пространства состояний связано с трудностью решения дифференциальных уравнений n-го порядка, описывающих движение системы в переменных «вход – выход», и с хорошо разработанными методами решения систем дифференциальных уравнений первого порядка.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 2.2.1

Определить переходные процессы в системе

      (2.2.1)

,                                (2.2.2)

под действием ступенчатых воздействий по каналам управления

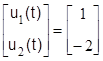 и возмущения .

Решение

В соответствии с выражениями (2.1.2), (2.1.3) запишем уравнение движения системы в интегральной форме

. (2.2.3)

Учитывая, что u(t)=u*1(t)=u, r(t)=r*1(t)=r и t₀=0, представим выражение (2.2.3) в виде

.     (2.2.4)

Для нахождения экспоненциала матрицы А определим корни характеристического уравнения 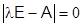, то есть

 и .

Так как корни различные действительные и матрица А диагональная, то ее экспоненциал равен

.               (2.2.5)

Подставляя выражения (2.2.5) в формулу (2.2.4) и последовательно проводя преобразования, получаем

=

.

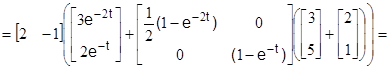
Следовательно, уравнение движения рассматриваемой системы в переменных «вход – выход» имеет вид:

.

УСТОЙЧИВОСТЬ

 

ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

 

Устойчивость или неустойчивость линейной многомерной системы (2.1.1) определяется ее свободным движением ( ), которое характеризуется собственными числами матрицы А, определяемыми из характеристического уравнения

 (3.1.1)

Линейная система (2.1.1) устойчива тогда и только тогда, когда все вещественные части собственных (характеристических) чисел λ_j=λ_j(A) (j=1,…,n) имеют неположительные значения, т.е. Reλ_j . Если Reλ_j<0, то система асимптотически устойчива.

Характеристическое уравнение (3.1.1) можно записать в виде

_ⁿ_^n-1_n_n0. (3.1.2)

Условия устойчивости для системы n-го порядка записываются в виде определителей Гурвица, получаемых из квадратной матрицы коэффициентов характеристического уравнения (3.1.2).

 

.

 

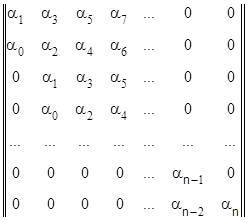Для устойчивости линейной системы по критерию Гурвица необходимо и достаточно, чтобы при α₀>0 были положительными и все n диагональных определителей Гурвица, то есть Δ_I>0 (i=l,...,n). Положительность последнего определителя Гурвица

Δ_n=α_nΔ_n-1                                     (3.1.3)

 

при Δ_n-1>0 сводится к положительности свободного члена α_n характеристического уравнения.

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 3.2.1

Определить устойчивость и характер свободного движения динамической системы, заданной в пространстве состояний векторными уравнениями

,                                                   (3.2.1)

.            (3.2.2)

 

Решение.

Запишем для системы (3.2.1) характеристическое уравнение (3.1.1)

,                                    (3.2.3)

решение которого дает следующие корни:

.

Рассматриваемая динамическая система является устойчивой. Ее свободное движение носит апериодический сходящийся характер, так как вещественные части корней характеристического уравнения отрицательные.

Задача 3.2.2

Определить устойчивость динамической системы, заданной в пространстве состояний векторно-матричными уравнениями

,            ,    (3.2.4)

.                           (3.2.5)

 

Решение.

Запишем для системы (3.2.4) характеристическое уравнение (3.1.1)

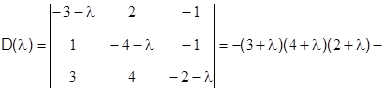
.      (3.2.6)

Раскроем скобки и приведем подобные члены, получим следующее характеристическое уравнение:

.                  (3.2.7)

Устойчивость системы будем определять на основе алгебраического критерия устойчивости Гурвица, составив для этого по уравнению (3.2.7) матрицу Гурвица

.               (3.2.8)

Для устойчивости линейной системы по критерию Гурвица необходимо и достаточно, чтобы при положительности коэффициента при старшей степени (в нашем случае коэффициент при λ³ равен 1) были положительными и все n диагональных определителей Гурвица, то есть Δ_i>0 (i=1,2,3)

, .

В соответствии с вышеизложенным находим, что свободный член характеристического уравнения (3.2.7) равный 54 - положительный.

Следовательно, система (3.2.4) является устойчивой.

УПРАВЛЯЕМОСТЬ