Основные методы математизации

Тот , кто не знает математики , не

может узнать никакой другой науки

и даже не может обнаружить своего

невежества .

Р . Бэкон

В чем же заключается мощь и удивительная плодотворность применения математики в различных науках? Чтобы ответить на этот вопрос, проанализируем некоторые методы математизации.

Важнейший метод – это математическое моделирование. Он состоит в том, что исследователь строит математическую модель рассматриваемой области, то есть выделяет существенные для него свойства и количественные характеристики явления, выделяет существенные отношения между ними и пытается найти какой-либо похожий объект в математике.

Например, изучая численности популяций сардин и рыб-хищников в Средиземном море, В.Вольтерра выделил следующие количественные характеристики:

· численность сардин (обозначив их за x)

· численность хищников (соответственно y)

далее он выявил важные для него отношения между ними:

· в среднем все особи одинаковы

· популяция сардин увеличивается, если нет встреч с хищником

· скорость роста ее численности пропорциональна самой численности (так как каждая особь может произвести потомство)

· число сардин, гибнущих от хищников пропорционально числу встреч с ними, а это число в среднем пропорционально xy

· популяция хищников уменьшается при отсутствии сардин (гибнут от голода)

· скорость этой убыли пропорциональна численности хищников

· скорость прироста числа хищников пропорциональна числу их встреч с кормом-сардинами, то есть величине xy.

Являясь крупным специалистом в теории дифференциальных уравнений, Вольтерра рассматривает x и  y как фунции от времени и быстро находит необходимый объект в математике – систему обыкновенных дифференциальных уравнений

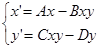
где A, B, C, D – некоторые положительные коэффициенты, зависящие от конкретных природных условий. Изучая затем эту систему методами, разработанными другими математиками задолго до него, Вольтерра получает описание и объяснение многих явлений, замеченных за долгую историю рыболовства в Италии, таких например, как странные колебания величины улова сардин (а значит и их общей численности).

Этот пример показывает еще одну идею моделирования – некоторое упрощение, отбрасывание лишней, не нужной информации. Здесь, это допущения одинаковости особей, равновероятности их встреч, равновозможности производить потомство. Мы как-будто бы абстрагируемся от конкретной сардины и выделяем только нужные для нас ее свойства. Конечно в итоге, мы получаем несколько упрощенную картину явления, но в данном случае нам это и требовалось. Важнейшим моментом является то, чтобы при упрощении не упустить нужные нам черты, не огрубить модель настолько, чтобы она перестала достаточно хорошо для нас описывать явление. С другой стороны, модель не должна получиться очень сложной, не поддающейся математическому анализу. Правда, с появлением мощных ЭВМ, возможности анализа заметно расширились, но некоторые задачи, например долгосрочное прогнозирование погоды, до сих пор являются недоступными.

Удивительным образом оказывается, что одна и та же математическая модель может описывать много разнообразных явлений в различных областях. Например, одно дифференциальное уравнение может описывать и рост численности популяции, и химический распад, и цепную ядерную реакцию, и распростронение информации в социальной группе. В чем причина такой всеприминимости математических моделей? Ответа на этот вопрос математика не дает. Вот что говорит академик В.И.Арнольд в лекции [2]:

Почему модель сечения конуса описывает движение планет ? Мистика . Загадка . Ответа на этот вопрос нет . Мы верим в силу рациональной науки . Ньютон видел в этом доказательство существования Бога :” Такое изящнейшее соединение Солнца , планет и комет не могло произойти иначе , как по намерению и по власти могущественного и премудрого существа … Сей управляет всем не как душа мира , а как властитель Вселенной , и по господству своему должен именоваться Господь Бог Вседержитель ”.

Но можно дать и следующее некоторое “обоснование” этому факту. Когда исследователь изучает какое-то явление и строит скажем количественную модель, он стремится к простоте модели и выделяет только небольшое число параметров и отношений между ними. В итоге, по огромному количеству явлений получаем модели, связанные скажем с определенными дифференциальными уравнениями. Но в теории дифференциальных уравнений эти уравнения классифицированы в достоточно небольшое число типов, которые различаются по свойствам и методам их решения. В итоге и получается, что дифференциальные уравнения (а значит и модели) для большого числа явлений попадают в один класс, в котором они практически неразличимы.

Помимо моделей, связанных с дифференциальными уравнениями, есть еще огромное число других моделей, в том числе и не количественных (то есть не связанных с какими-либо числовыми параметрами). Например, в математической логике и теории алгоритмов существует модель, описывающая работу человека, решающего какую-нибудь проблему по строго описанной программе (рецепту). Эта модель называется машиной Тьюринга и придумана в 1936 году английским математиком Аланом Тьюрингом в связи с проблемой формализации понятия алгоритма. Она оказалась очень полезной для разработки первых ЭВМ, и с тех пор является общепринятой математической моделью современных компьютеров.

Тьюринг исходил из следующих упрощений:

· в процессе работы, человек (компьютер) имеет дело с наборами символов (словами) из конечного множества (алфавита)

· в начале работы на некотором носителе информации, например в тетради (ленте) записан вход

· в конце работы, на ленте пишется выход

· лента разделена на ячейки, каждая либо пуста, либо там есть один символ алфавита

· лента потенциально бесконечна и одномерна (то есть каждая ячейка имеет двух соседей: правого и левого)

· в процессе работы человек может за один шаг записывать символ в текущую ячейку (если она занята, то предварительно стереть содержимое) и читать его, а также сдвигаться вправо или влево

· все вышеописанные действия он выполняет в строгом соответствии с программой, которая по текущему обозреваемому символу и текущему состоянию человека (их конечное число) говорит, какой символ записать в ячейку, куда сдвинуться (вправо или влево) и как сменить состояние

· человек останавливает вычисления, когда попадает в некоторое выделенное состояние (заключительное)

Откуда такая модель могла возникнуть? Например из анализа работы математика, который что-то решает в тетради: на первых страницах записано условие задачи – слово в достаточно большом (но конечном!) алфавите; далее он согласно некоторым правилам своей науки (программе!) и своему внутреннему состоянию (этих состояний много, но конечно), листая тетрадь то вперед, то назад, записывая и стирая символы, постепенно решает задачу. Попав в заключительное состояние (поняв, что ответ найден), он останавливается. Есть и возможность того, что он никогда не остановится – модель это не запрещает.

Удивительно то, что эта простая модель, прекрасно описывающая работу современных компьютеров, родилась раньше, чем появились первые ЭВМ.

Из каких этапов состоит построение математической модели? Это зависит, вообще говоря, от области, в которой разрабатывается эта модель. Например, в экономике этапы можно выделить такие [3]:

1. Определение цели, то есть чего хотят добиться, решая поставленную задачу.

2. Определение параметров модели, то есть заранее известных фиксированных факторов, на значение которых исследователь не влияет.

3. Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.

4. Определение области допустимых решений, то есть тех ограничений, которым должны удовлетворять управляющие переменные.

5. Выявление неизвестных факторов, то есть величин, которые могут изменяться случайным или неопределенным образом.

6. Выражение цели через управляющие переменные, параметры и неизвестные факторы, то есть формирование целевой функции, называемой также критерием оптимальности задачи.

Это связано со спецификой области: в экономике важны именно такие числовые модели, так как предметная область там в основном состоит из понятий, которые имеют количественный характер. Такие примеры, как машина Тьюринга под эту схему не подходят.

Итак, основные черты метода математического моделирования заключатся в следующем:

· абстракция, некоторое упрощение предметной области, выделение только существенных для исследователя черт рассматриваемого явления

· выявление нужных параметров или характеристик процесса, которые и составляют предмет дальнейшего исследования

· выявление существенных взаимоотношений между этими параметрами

· поиск нужного математического объекта, который будет описывать все исследуемые параметры и отношения между ними

· применение математического аппарата к этому объекту для описания исходного явления

Выражаясь математическим языком, можно сказать, что происходит отображение предметной области, реального явления в математические множества (понятия, структуры). Причем это отображение обладает свойством сохранять некоторые отношения между реальными объектами, в том смысле, что при изменении в реальности происходит похожее изменение и в математическом ее образе.

Не следует думать, что математика всегда располагает необходимым аппаратом для исследования математической модели. Зачастую приходилось открывать новые понятия и методы в математике или разрабатывать старые, чтобы делать это. Например, Ньютон открыл основные понятия дифференциального исчисления, чтобы как раз использовать их в механике. И вообще большинство областей современной математики имеют такое практическое происхождение.

Очень интересен также следующий вопрос: почему же математические модели, сам математический язык настолько полезен для изучения многих явлений в различных науках? Я считаю, что это отчасти связано с непревзойденной строгостью и точностью математического языка, отчасти с его эффективностью и сжатостью. Профессор А.К.Гуц в [4] иллюстрировал эту эффективность следующим отличием гуманитарного мышления от математического. Когда гуманитарий решает какую-нибудь проблему, на пути к ее решению он должен пройти очень большое число промежуточных этапов, на каждом из которых делаются, анализируются и проверяются какие-то логические выводы. Это можно изобразить на диаграмме:

Так как таких промежуточных шагов может быть много, путь к решению может занять очень много времени. Теперь рассмотрим решение задачи математиком. Движение его к цели по сути тоже заключается в серии промежуточных шагов, но он может применять теоремы, формулы, факты установленные и проверенные другими математиками, которые заключают в себе сотни, тысячи элементарных логических шагов, которые уже нет необходимости проделывать. Его путь можно изобразить такой диаграммой:

 

здесь “сгустки” – это факты, проверенные другими. Поэтому за тот же промежуток времени математик может сделать гораздо больше.

Адекватность математики при отражении реальности в своих моделях связана с тем, что сама математика, ее понятия и структуры являются не чем иным, как абстракцией самой объективной реальности. Когда мы создаем какое-то множество математических понятий, абстрагируясь от реальных объектов, мы неявно переносим в понятия и связи между этими объектами, которые затем возникают при построении математических моделей. Например, при выделении понятия “натуральное число” как абстракции свойств реальных объектов быть элементом некоторого набора однородных предметов, которые можно переложить один за другим из одной кучки в другую, мы переносим в абстракцию и некоторые свойства натуральных чисел, такие как упорядоченность чисел. При “моделировании” затем скажем коллектива людей, исследуем численность коллектива x (натуральное число)и обнаруживаем, что при добавлении одного индивида, коллектив увеличивается, но увеличивается при этом на 1 и x – мы неявно перенесли упорядоченность реального объекта “коллектив” на его математическую модель “натуральнозначная переменная”. Выдающийся физик, лауреат Нобелевской премии, Поль Дирак говорил: “ При построении физической теории следует не доверять всем физическим концепциям . … Следует доверять математической схеме , даже если она , на первый взгляд , не связана с физикой ”.

Можно отдельно выделить метод математизации, который неявно является частью математического моделирования: формализация. Он состоит в том, что все изучаемые объекты реальности и отношения между ними заменяются наборами символов и отношений между ними в некотором искусственном языке. Так, в модели машины Тьюринга все объекты – слова в каком-то алфавите, и рассматриваются правила работы с этими словами. Да и вообще, система удобных обозначений – важная часть любой области математики. Этот искусственный язык должен быть по возможности компактным, недвусмысленным и простым. Это отличает его от естественных человеческих языков, для которых характерна некоторая неоднозначность и неопределенность семантики и синтаксиса. Недаром до сих пор не создано удовлетворительных автоматических систем перевода с одного языка на другой. Поэтому важнейшей частью формализации является правильный перевод предметной области на формальный язык. Как пишет Герман Вейль в [6]: “ Мощь науки, как свидетельствует развитие современной техники, опирается на комбинацию априорных знаковых конструкций и систематического опыта в форме планируемых и воспроизводимых экспериментов и соответствующих измерений. ” В самой математике процесс формализации начался еще с древнегреческого математика Диофанта, который предложил некоторую еще несовершенную систему алгебраических обозначений. Привычные нам обозначения основных математических объектов вводились постепенно, начиная с Виета, Декарта, Лейбница и заканчивая Эйлером, Лагранжем, Коши. Этот процесс продолжается до сих пор, так как каждый день возникают новые и новые математические понятия и объекты.

В конце XIX – начале XX века процесс формализации математики достиг своей кульминации в трудах Фреге, Рассела, Гильберта и др. Это связано с так называемой программой Гильберта обоснования математики. В чем она состоит? Хотя математику и математические рассуждения принято считать логически строгими и безупречными, работающие математики никогда не проводят доказательства своих теорем на формальном уровне, сравнимом например с алгоритмическими языками программирования типа C или PASCAL, то есть так, чтобы правильность доказательства мог бы проверить компьютер. Поэтому Гильберт и его коллеги решили построить такой формальный язык с соответствующими правилами, в котором можно было выразить и доказать все математические теоремы. В основу этого языка была положена логика, основными объектами стали множества, которые обозначались символами в конечном алфавите. Отталкиваясь от некоторых простейших утверждений – аксиом, примменяя некоторые строго очерченные правила вывода, можно было бы получить все утверждения математики. Если бы эта программа удалась, то всех математиков можно было бы заменить компьютерами, которые бы чисто механически шаг за шагом получали бы математические теоремы.

Прежде чем описать причины краха программы Гильберта, выделим еще один метод математизации, который тесно связан с этой программой. Речь идет об аксиоматизации. Она состоит в том, что в некоторой области знания из всех истинных утверждений выделяется набор некоторых простейших утверждений или аксиом, из которых посредством логического вывода можно в принципе получить любое утверждение этой области. Конечно, желательно чтобы этот набор был достаточно компактным (хотя бы конечным) и простым. Классическим примером аксиоматически построенной теории является геометрия Евклида (хотя у него список аксиом был неполный). Конституция государства и всевозможные кодексы в некотором смысле являются списками аксиом в юриспруденции. Правила дорожного движения есть ни что иное, как аксиомы теории правильного уличного движения. Со времен Евклида аксиоматический метод построения теории стал эталоном. Аксиоматизировать пытались и такие неточные науки, как этика (Спиноза). Пожалуй наиболее удачным примером аксиоматизации является построение механики Ньютоном на основе выделенных им 3 законов. Конечно, не следует считать, что этих 3 аксиом достаточно для построения механики – к этому списку необходимо добавить все аксиомы трехмерной геометрии, теории действительных чисел и, если уж быть окончательно строгим, то и в самой логике можно выделить тоже некоторые аксиомы. Дальнейшее развитие физики добавляло еще аксиомы: законы термодинамики, электромагнетизма, постулаты Эйнштейна в теории относительности и законы квантовой механики. Но принцип оставался тот же – добавляются по возможности простейшие и независимые от предыдущих факты, из которых можно объяснить как можно больше новых явлений. Продолжалась и продолжается аксиоматизация в самой математике: с помощью аксиомам в алгебре определяются важнейшие понятия группы, поля, кольца; аксиоматика Колмогорова сделала теорию вероятностей математической наукой.

Вернемся теперь к программе Гильберта. Она, кроме формализации и выделения основных понятий, включала в себя аксиоматизацию всей математики на основе аксиом арифметики и теории множеств. В трудах многих математиков был найден подходящий список аксиом и правил вывода (одно из которых - правило modus ponens, описанное еще Аристотелем), из которого выводились все известные факты математики. Оставались неясными два вопроса:

· Будет ли этот список аксиом непротиворечивым? То есть не существует ли такого утверждения, что из аксиом можно вывести его само и его отрицание? Известно, что в этом случае можно будет вывести любое утверждение – это разрушит авторитет математики как эталона строгости, сделает бессмысленной и ненужной данную систему аксиом.

· Будет ли этот система аксиом полной? То есть любая ли математическая истина может быть получена из данных аксиом с помощью последовательных логических выводов? Это означает, что любое утверждение мы можем либо доказать, либо опровергнуть (доказать его отрицание).

Математики и логики, воодушевленные первыми успехами программы Гильберта, принялись искать доказательство полноты и непротиворечивости арифметики – промежуточного шага на пути ко всей математике. Было достигнуто несколько обнадеживающих результатов. Казалось, цель была близка. Но в 1931 году грянул гром, который обратил программу Гильберта в руины: австрийский логик Курт Гёдель доказал так называемую теорему о неполноте, которая утверждала, что если система аксиом арифметики непротиворечива, то существует такое утверждение, что ни оно само, ни его отрицание не доказуемы. Это означает, что условия непротиворечивости и полноты арифметики и математики в целом несовместны. Более того, она остается неполной, если к списку добавить дополнительные аксиомы (любое конечное число), то есть не существует конечного набора аксиом для арифметики. Это был шок. Один математик в связи с этим сказал: “ Бог существует , потому что математика непротиворечива . Дьявол существует , потому что мы это не можем доказать ”. Теорема Гёделя показала пределы возможностей аксиоматического метода в самой математике.

Нужно все-таки сказать, что это был крах некоторого идеала, который на самом деле  не оказал большого влияния на практические приложения математики. Системы аксиом арифметики и теории множеств до сих пор являются основанием математического знания. Аксиомы в различных областях знания не потеряли своей ценности.