 |
Главная |
Сферическая тригонометрия
|
из
5.00
|
Свойства функции синус
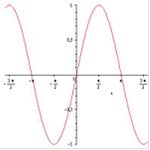
Синус
1. Область определения функции - множество всех действительных чисел: 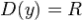 .
.
2. Множество значений - промежуток [−1; 1]:  = [−1;1].
= [−1;1].
. Функция  является нечётной:
является нечётной:  .
.
. Функция периодическая, наименьший положительный период равен 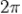 :
:  .
.
. График функции пересекает ось Ох при  .
.
. Промежутки знакопостоянства:  при
при  и
и  при
при  .
.
. Функция непрерывна и имеет производную при любом значении аргумента: 
. Функция  возрастает при
возрастает при 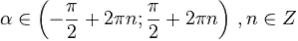 , и убывает при
, и убывает при  .
.
. Функция имеет минимум при  и максимум при
и максимум при  .
.
Свойства функции косинус

Косинус
1. Область определения функции - множество всех действительных чисел: 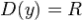 .
.
2. Множество значений - промежуток [−1; 1]:  = [−1;1].
= [−1;1].
. Функция  является чётной:
является чётной:  .
.
. Функция периодическая, наименьший положительный период равен 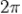 :
:  .
.
. График функции пересекает ось Ох при  .
.
. Промежутки знакопостоянства:  при
при 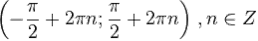 и
и  при
при 
. Функция непрерывна и имеет производную при любом значении аргумента: 
. Функция  возрастает при
возрастает при  и убывает при
и убывает при 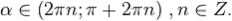
. Функция имеет минимум при  и максимум при
и максимум при 
Свойства функции тангенс
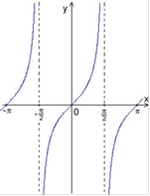
Тангенс
1. Область определения функции - множество всех действительных чисел: 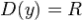 , кроме чисел
, кроме чисел 
2. Множество значений - множество всех действительных чисел: 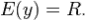
. Функция 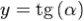 является нечётной:
является нечётной:  .
.
. Функция периодическая, наименьший положительный период равен  :
: 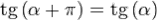 .
.
. График функции пересекает ось Ох при  .
.
. Промежутки знакопостоянства:  при
при  и
и  при
при 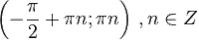 .
.
. Функция непрерывна и имеет производную при любом значении аргумента из области определения: 
. Функция  возрастает при
возрастает при  .
.
Свойства функции котангенс
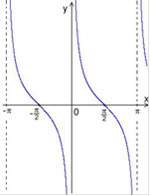
Котангенс
1. Область определения функции - множество всех действительных чисел:  кроме чисел
кроме чисел 
2. Множество значений - множество всех действительных чисел: 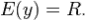
. Функция  является нечётной:
является нечётной: 
. Функция периодическая, наименьший положительный период равен  :
: 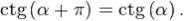
. График функции пересекает ось Ох при 
. Промежутки знакопостоянства:  при
при  и
и  при
при 
. Функция непрерывна и имеет производную при любом значении аргумента из области определения: 
. Функция  убывает при
убывает при 
Стандартные тождества
Тождества - это равенства, справедливые при любых значениях входящих в них переменных.



Формулы преобразования суммы углов.
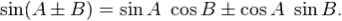



Общие формулы

Треугольник со сторонами a, b, c и соответственно противоположные углами A, B, C. В следующих тождествах, A, B и C являются углами треугольника; a, b, c - длины сторон треугольника, лежащие напротив соответствующих углов.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника <http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA>
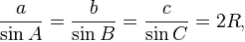
где  - радиус окружности, описанной вокруг <http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C> треугольника.
- радиус окружности, описанной вокруг <http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C> треугольника.

Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами 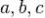 и углом
и углом  , противолежащим стороне
, противолежащим стороне  ,
,


Теорема тангенсов

Формула Эйлера
Формула Эйлера утверждает, что для любого действительного числа <http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE> 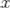 выполнено следующее равенство:
выполнено следующее равенство:

где  - основание натурального логарифма <http://ru.wikipedia.org/wiki/E_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BA%D0%BE%D0%BD%D1%81%D1%82%D0%B0%D0%BD%D1%82%D0%B0)>,
- основание натурального логарифма <http://ru.wikipedia.org/wiki/E_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BA%D0%BE%D0%BD%D1%81%D1%82%D0%B0%D0%BD%D1%82%D0%B0)>,  - мнимая единица.
- мнимая единица.
Формула Эйлера предоставляет связь между математическим анализом <http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7> и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы <http://ru.wikipedia.org/wiki/%D0%92%D0%B5%D1%81%D0%BE%D0%B2%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F> экспоненциальной функции:

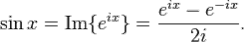
Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера:


с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

5. Решение простых тригонометрических уравнений

Если  - вещественных решений нет.
- вещественных решений нет.
Если  - решением является число вида
- решением является число вида 

Если  - вещественных решений нет.
- вещественных решений нет.
Если  - решением является число вида
- решением является число вида 
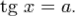
Решением является число вида 

Решением является число вида 
6. Тригонометрические формулы
Основные тригонометрические тождества.
sin² α + cos² α = 1α · ctg α = 1
tg α = sin α ÷ cos αα = cos α ÷ sin α
1 + tg² α = 1 ÷ cos² α
1 + ctg² α = 1 ÷ sin² α
Формулы сложения.
(α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
Формулы двойного угла.
cos 2α = cos² α - sin² α
cos 2α = 2cos² α - 12α = 1 - 2sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)
Формулы тройного угла.
sin 3α = 3sin α - 4sin³ α3α = 4cos³ α - 3cos α3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)
Формулы понижения степени.
sin² α = (1 - cos 2α) ÷ 2
sin³ α = (3sin α - sin 3α) ÷ 4
cos² α = (1 + cos 2α) ÷ 2
cos³ α = (3cos α + cos 3α) ÷ 4
sin² α · cos² α = (1 - cos 4α) ÷ 8
sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32
Переход от произведения к сумме.
α · cos β = ½ (sin (α + β) + sin (α - β))
sin α · sin β = ½ (cos (α - β) - cos (α + β))
cos α · cos β = ½ (cos (α - β) + cos (α + β))
Переход от суммы к произведению.
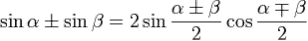
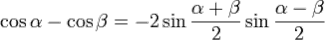
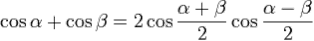

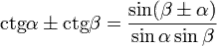
Сферическая тригонометрия
Важным частным разделом тригонометрии, используемым в астрономии, геодезии, навигации и других отраслях, является сферическая тригонометрия, рассматривающая свойства углов между большими кругами на сфере и дуг этих больших кругов. Геометрия сферы существенно отличается от евклидовой планиметрии; так, сумма углов сферического треугольника, вообще говоря, отличается от 180°, треугольник может состоять из трёх прямых углов. В сферической тригонометрии длины сторон треугольника (дуги больших кругов сферы) выражаются посредством центральных углов, соответствующих этим дугам. Поэтому, например, сферическая теорема синусов <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D1%81%D0%B8%D0%BD%D1%83%D1%81%D0%BE%D0%B2_(%D1%81%D1%84%D0%B5%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)> выражается в виде:

и существуют две теоремы косинусов <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81%D0%BE%D0%B2_(%D1%81%D1%84%D0%B5%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)>, двойственные друг другу.
8. Применение тригонометрических вычислений
Тригонометрические вычисления применяются практически во всех областях геометрии <http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F>, физики <http://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0> и инженерного дела <http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D0%B6%D0%B5%D0%BD%D0%B5%D1%80%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B5%D0%BB%D0%BE>. Большое значение имеет техника триангуляции <http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B0%D0%BD%D0%B3%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F_(%D0%B3%D0%B5%D0%BE%D0%B4%D0%B5%D0%B7%D0%B8%D1%8F)>, позволяющая измерять расстояния до недалёких звёзд <http://ru.wikipedia.org/wiki/%D0%97%D0%B2%D0%B5%D0%B7%D0%B4%D0%B0>в астрономии <http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D1%8F>, между ориентирами в географии <http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D1%83%D0%B7%D1%8B%D0%BA%D0%B8>, акустика <http://ru.wikipedia.org/wiki/%D0%90%D0%BA%D1%83%D1%81%D1%82%D0%B8%D0%BA%D0%B0>, оптика <http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D0%BA%D0%B0>, анализ финансовых рынков, электроника <http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%B8%D0%BA%D0%B0>, теория вероятностей <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9>, статистика <http://ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0>, биология <http://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, медицина <http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D0%B4%D0%B8%D1%86%D0%B8%D0%BD%D0%B0> (включая ультразвуковое исследование <http://ru.wikipedia.org/wiki/%D0%A3%D0%BB%D1%8C%D1%82%D1%80%D0%B0%D0%B7%D0%B2%D1%83%D0%BA%D0%BE%D0%B2%D0%BE%D0%B5_%D0%B8%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5> (УЗИ) и компьютерную томографию <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D0%BC%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>), фармацевтика <http://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D1%80%D0%BC%D0%B0%D1%86%D0%B5%D0%B2%D1%82%D0%B8%D0%BA%D0%B0>, химия <http://ru.wikipedia.org/wiki/%D0%A5%D0%B8%D0%BC%D0%B8%D1%8F>, теория чисел <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%B5%D0%BB> (и, как следствие, криптография <http://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>), сейсмология <http://ru.wikipedia.org/wiki/%D0%A1%D0%B5%D0%B9%D1%81%D0%BC%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, метеорология <http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%B5%D0%BE%D1%80%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, океанология <http://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D0%B5%D0%B0%D0%BD%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, картография <http://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D1%80%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>, многие разделы физики <http://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0>, топография и геодезия <http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%B4%D0%B5%D0%B7%D0%B8%D1%8F>, архитектура <http://ru.wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D1%82%D0%B5%D0%BA%D1%82%D1%83%D1%80%D0%B0>, фонетика <http://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D0%BD%D0%B5%D1%82%D0%B8%D0%BA%D0%B0>, экономика <http://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D0%BA%D0%B0>, электронная техника <http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D0%B0>, машиностроение <http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5>, компьютерная графика <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%B0>, кристаллография <http://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>.
Существует множество областей, в которых применяются тригонометрия и тригонометрические функции <http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8>. Например, метод триангуляции <http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B0%D0%BD%D0%B3%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F_(%D0%B3%D0%B5%D0%BE%D0%B4%D0%B5%D0%B7%D0%B8%D1%8F)> используется в астрономии <http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC> для измерения расстояния до ближайших звезд, в географии <http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%B3%D1%80%D0%B0%D1%84> для измерения расстояний между объектами, а также в спутниковых навигационных системах <http://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D1%83%D1%82%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BD%D0%B0%D0%B2%D0%B8%D0%B3%D0%B0%D1%86%D0%B8%D0%B8>. Синус <http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BD%D1%83%D1%81> и косинус <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81> имеют фундаментальное значение для теории периодических функций <http://ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B8%D0%BE%D0%B4%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F>, например при описании звуковых и световых волн.
Тригонометрия или тригонометрические функции используются в астрономии <http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC> (особенно для расчётов положения небесных объектов <http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BE%D0%B1%D1%8A%D0%B5%D0%BA%D1%82>, когда требуется сферическая тригонометрия <http://ru.wikipedia.org/wiki/%D0%A1%D1%84%D0%B5%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F>), в морской и воздушной навигации, в теории музыки <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D1%83%D0%B7%D1%8B%D0%BA%D0%B8>, в акустике <http://ru.wikipedia.org/wiki/%D0%90%D0%BA%D1%83%D1%81%D1%82%D0%B8%D0%BA%D0%B0>, в оптике <http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D0%BA%D0%B0>, в анализе финансовых рынков <http://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BD%D0%B0%D0%BD%D1%81%D0%BE%D0%B2%D1%8B%D0%B9_%D1%80%D1%8B%D0%BD%D0%BE%D0%BA>, в электронике, в теории вероятностей <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9>, в статистике, в биологии <http://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, в медицинской визуализации (например, компьютерная томография <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D0%BC%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F> и ультразвук <http://ru.wikipedia.org/wiki/%D0%A3%D0%BB%D1%8C%D1%82%D1%80%D0%B0%D0%B7%D0%B2%D1%83%D0%BA>), в аптеках, в химии, в теории чисел <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%B5%D0%BB> (следовательно, и в криптологии <http://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>), в сейсмологии <http://ru.wikipedia.org/wiki/%D0%A1%D0%B5%D0%B9%D1%81%D0%BC%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, в метеорологии <http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%B5%D0%BE%D1%80%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, в океанографии <http://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D0%B5%D0%B0%D0%BD%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F>, во многих физических науках, в межевании <http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D0%B6%D0%B5%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5> и геодезии <http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%B4%D0%B5%D0%B7%D0%B8%D1%8F>, в архитектуре <http://ru.wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D1%82%D0%B5%D0%BA%D1%82%D0%BE%D1%80>, в фонетике <http://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D0%BD%D0%B5%D1%82%D0%B8%D0%BA%D0%B0>, в экономике <http://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D0%BA%D0%B0>, в электротехнике <http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D0%B0>, в машиностроении <http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5>, в гражданском строительстве, в компьютерной графике <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%B0>, в картографии <http://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D1%80%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>, в кристаллографии <http://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F>, в разработке игр и многих других областях.

|
из
5.00
|
Обсуждение в статье: Сферическая тригонометрия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

