 |
Главная |
Элементы векторной алгебры и аналитической геометрии
|
из
5.00
|
Задача 1. Даны векторы a, b, c, d. Для указанных в пп. 1-3 векторов требуется:
) вычислить скалярное произведение векторов из пункта; 2) найти модуль векторного произведения векторов; 3) проверить коллинеарность и ортогональность векторов; 4) убедиться, что векторы a,b,c образуют базис; 5) найти координаты вектора d в этом базисе.
a=10i+3j+k, b=i+4j+2k, c=3i+9j+2k, d=19i+30j+7k;
1) -7a, 4c; 2) 3a, 7b; 3) a, c.
. Вычислить скалярное произведение векторов из пункта:

) найти модуль векторного произведения векторов;
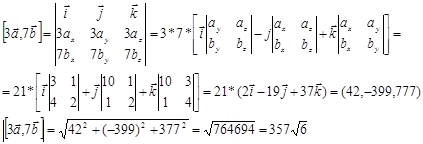
) проверить коллинеарность и ортогональность векторов 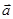 и
и  ;
;
Вектора коллиниарны  если
если
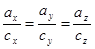 ,
,
или векторное произведение  :
:
 ,
,
т.е. вектора 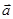 и
и  неколлиниарны.
неколлиниарны.
Вектора 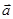 и
и  перпендикулярны
перпендикулярны  если их скалярное произведение
если их скалярное произведение  .
.
Т.е. 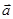 и
и  неперпендикулярны.
неперпендикулярны.
) Убедиться, что векторы a,b,c образуют базис;
a=10i+3j+k, b=i+4j+2k, c=3i+9j+2k
В пространстве образует базис любая тройка некомпланарных векторов. Вектора некомпланарны, когда их смешанное произведение не равно 0;

Следовательно вектора образуют базис.
) Найти координаты вектора d=19i+30j+7k в базисе векторов a,b,c.
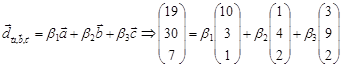
Получили систему:

Решим систему методом Крамера:
 ,
,  ,
,  ,
, 
 ;
;  ;
; 

Задача 2. Даны вершины A(x1, y1), B(x2, y2), C(x3, y3) треугольника ABC.
Требуется найти:
уравнение стороны AB;
Уравнение прямой, проходящей через две точки А и В имеет вид:
АВ: 
уравнение высоты CH и длину этой высоты;
Общее уравнение прямой имеет вид:
 , где
, где  - координаты вектора нормали.
- координаты вектора нормали.
Определим a и b для прямой АВ:

Вектор нормали  одновременно является направляющим вектором прямой СН. Тогда каноническое уравнение высоты будет иметь вид (с учетом того, что прямая проходит через точку
одновременно является направляющим вектором прямой СН. Тогда каноническое уравнение высоты будет иметь вид (с учетом того, что прямая проходит через точку 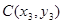 ):
):

Длина высоты СН равна модулю проекции вектора АС или ВС на направление вектора


уравнение меидианы AM;
Определим координаты точки М:

Тогда уравнение АМ, проходящей через 2 точки имеет вид:

точку N пересечения медианы AM и CH;


уравнение прямой, параллельной стороне AB и проходящей через вершину C;
Вектор 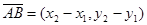
Тогда каноническое уравнение искомой прямой будет иметь вид:
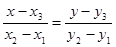
) внутренний угол при вершине A и внешний угол при вершине C.
A(-2,-3), B(1,6), C(6,1).
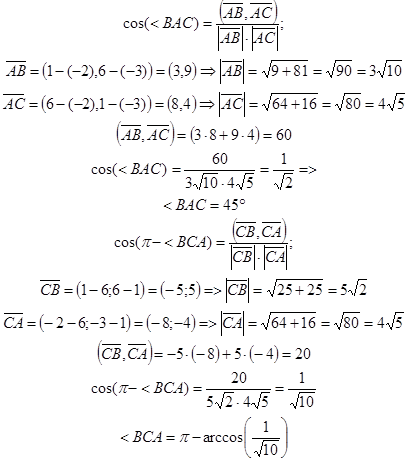
Задача 3. Составить канонические уравнения 1) эллипса, 2) гиперболы, 3) параболы по известным из условий 1 - 3 параметрам. Через a и b обозначены большая и малая полуоси эллипса или гиперболы, через F - фокус кривой,  - эксцентриситет, 2 c - фокусное расстояние,
- эксцентриситет, 2 c - фокусное расстояние,  - уравнения асимптот гиперболы, D - директриса кривой, A, B- точки, лежащие на кривой.
- уравнения асимптот гиперболы, D - директриса кривой, A, B- точки, лежащие на кривой.
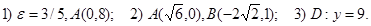
Составить каноническое уравнение эллипса, если 
Каноническое уравнение эллипса имеет вид:
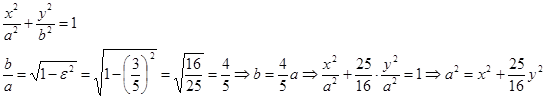
Подставим координаты точки А в уравнение и получим:
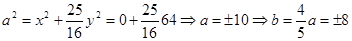
Искомое каноническое уравнение эллипса имеет вид:

Составить каноническое уравнение гиперболы, если
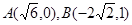
Каноническое уравнение гиперболы имеет вид:

Точка А является одной из точек пересечения гиперболы с осью ОХ. Следовательно  .
.
Зная точку В найдем фокусное расстояние с гиперболы.

Следовательно, уравнение искомой гиперболы будет иметь вид:
вектор произведение эллипс гипербола

Составить каноническое уравнение параболы, если известна директриса 
Каноническое уравнение искомой параболы имеет общий вид: 
Директриса записывается виде
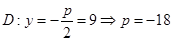
Следовательно искомое уравнение имеет вид: 
Задачи 4. Даны четыре точки A1(x1,y1,z1), A2(x2,y2,z2), A3(x3,y3,z3), A4(x4,y4,z4). Требуется найти:
) уравнение плоскости A1A2A3;
Уравнение плоскости, проходящей через 3 точки имеет вид:

2) уравнение прямой, проходящей через точку A4, перпендикулярно плоскости A1A2A3;
Направляющий вектор прямой совпадает с вектором нормали плоскости A1A2A3 координаты которых определяются как
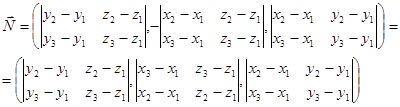
Каноническое уравнение искомой прямой принимает вид:
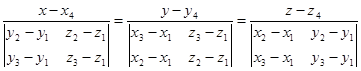
расстояние от точки A4 до плоскости A1A2A3 находится как:
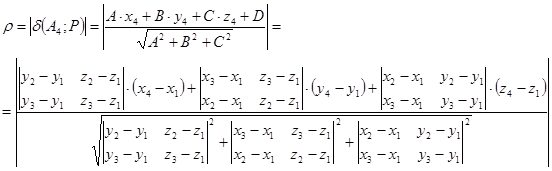
синус угла между прямой A1A4 и плоскостью A1A2A3;Уравнение прямой A1A4 имеет вид:

Направляющий вектор прямой A1A4  . Тогда
. Тогда

) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3. A1(7,5,3), A2(9,4,4), A3(4,5,7), A4(7,9,6).
Косинус угла между плоскостями определяется как косинус угла между его нормалями:


|
из
5.00
|
Обсуждение в статье: Элементы векторной алгебры и аналитической геометрии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

