Теорема о непрерывности суперпозиции функций и её следствия (перестановка предела и непрерывной функции).

Числовая последовательность и её предел. Теорема Бернулли об ограниченной

Последовательности

Теорема Бернулли об ограниченной Последовательности Если последовательность xn , n принадлежит N сходится ,то она ограничена

Признак Больцано-Коши сходимости (критерий Коши сходимости последовательности).

Последовательность {x_n} удовлетворяет условию Коши, если для любого положительного действительного числа ε > 0 существует такое натуральное число N_ε, что
(1) |x_n – x_m| < ε при n > N_ε , m > N_ε.

Последовательности, удовлетворяющие условию Коши, также называют фундаментальными последовательностями.

Условие Коши можно представить и в другом виде. Пусть m > n. Если m < n, то поменяем n и m местами. Случай нас не интересует, поскольку при этом неравенство (1) выполняется автоматически. Имеем :;Здесь p – натуральное число.

Тогда условие Коши можно сформулировать так: Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что
(2) при и любых натуральных p. Число , фигурирующее в условии Коши, зависит от ε. То есть оно является функцией от действительной переменной ε, областью значений которой является множество натуральных чисел. Число также можно записать в виде , как это принято для обозначения функций.

Критерий Коши сходимости последовательности

Критерий Коши сходимости последовательности

Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Теорема Больцано-Вейерштрасса о подпоследовательности.

Теорема Больцано – Вейерштрасса

Из любой ограниченной последовательности действительных чисел можно выделить подпоследовательность, сходящуюся к конечному числу. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся 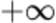к или к   .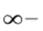

Теорему Больцано – Вейерштрасса можно сформулировать и так.

Из любой последовательности действительных чисел можно выделить подпоследовательность, сходящуюся или к конечному числу, и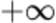ли к или к  .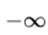

4 Теорема о пределах композиций пределов (сумма, разность, умножение, деление)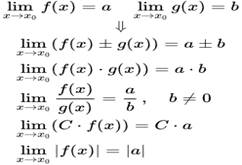

Первый замечательный предел и его следствия.

6 Второй замечательный предел и его следствия.

Предел функции и непрерывность. Теорема о непрерывности композиций (сумма,

Разность, произведение, деление).

Теорема о непрерывности суперпозиции функций и её следствия (перестановка предела и непрерывной функции).

Т: Пусть функция φ(y) определима в промежутке y, а ф-ция f(x) – в промежутке x, причем значение последовательности функции не выходит за пределы Y, когда x изменяется в Х.

Если f(x) непрерывна в точке x₀ и x, а φ(y) непрерывна в соотв. точках y₀=f(x) и y, то и сложная функция φ(f(x)) будет непрерывна в точке x₀.

Док-во: ξ>0, так как φ(y) непрерывна при y=y₀, то по ξ найдется такое Δ>0, что из |x-x₀|<Δ следует |φ(y)-φ(y₀)|<ξ

С другой стороны ввиду непрерывности f(x) при x=x₀ по Δ найдется такое Δ>0, что из |x-x₀|<Δ след. |f(x)-f(x₀)|=|f(x)-y₀|<Δ => |φ(f(x))-φ(y₀)|=|φ(f(x))-φ(f(x₀))|≤Δ след. φ(f(x)) непрерывная в точке x₀.