 |
Главная |
II. Поле алгебраических чисел.
|
из
5.00
|
Содержание.
1. Введение......................................................................................................................... 2
2. I. Краткий исторический очерк............................................................................ 3
3. II. Поле алгебраических чисел............................................................................. 4
4. 2.1. Понятие числового поля................................................................................ 4
5. 2.2. Алгебраическое число.................................................................................... 5
6. 2.3. Поле алгебраических чисел.......................................................................... 11
7. III. Рациональные приближения алгебраических чисел........................... 14
8. 3.1 Теорема Лиувиля................................................................................................ 14
9. 3.2 Трансцендентные числа Лиувиля................................................................ 16
10. Заключение............................................................................................................................................ 18
Курсовая по алгебре
Тема: «Алгебраические числа»
Введение.
Первоначальные элементы математики связаны с появлением навыков счета, возникающих в примитивной форме на сравнительно ранних ступенях развития человеческого общества, в процессе трудовой деятельности.
Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел рассматриваются не только натуральные числа, но и множество всех целых чисел, а так же множество рациональных чисел.
Если рассматривать корни многочленов: f(x)=xn+a1xn-1+…+an с целыми коэффициентами, то обычные целые числа соответствуют случаю, когда этот многочлен имеет степень n=1. Во множестве комплексных чисел естественно выделить так называемые целые алгебраические числа, представляющие собой корни многочленов с целыми коэффициентами.
Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел. Она связана с изучением различных классов алгебраических чисел.
I . Краткий исторический очерк.
Огромное значение в развитии теории чисел имели замечательные работы К. Гаусса (1777-1855). Гаусс наряду с изучением обычных чисел начал рассматривать так же и арифметику чисел, получивших название целых гауссовских чисел, а именно числа вида a+bi, где a и b – обычные целые числа. Эти его исследования положили начала алгебраической теории чисел.
Теория алгебраических чисел была построена в работах Куммера (1810-1893) и Дирихле (1805-1859) и развита затем Кронекером (1823-1891), Дедекиндом (1831-1916) и Е.И. Золотаревым (1847-1878). Работы Лиувилля (1809-1882) и Эрмита (1822-1901) явились основой трансцендентных чисел.
Вопросы аппроксимации алгебраических чисел рациональными были существенно продвинуты в начале века А. Туэ, а затем в пятидесятых годах в работах К. Рота.
В последнее время все большее внимание специалистов по теории чисел привлекает алгебраическая теория чисел.
Здесь надо назвать работы Г. Хассе, Е. Гекке, а в особенности французского математика А. Вейля, результаты которого были использованы во многих теорико-числовых исследованиях, как например Д. Берджессом в проблеме о наименьшем квадратичном вычете.
К алгебраической теории чисел относятся и интересные работы советского математика И.Р. Шафаревича, а так же работы Б.Н. Делонга по теории кубических форм.
II. Поле алгебраических чисел.
2.1 Понятие числового поля
Естественный и важный подход к выделению и изучению тех или иных множеств чисел связан с замкнутостью множеств чисел относительно тех или иных действий.
Определение 1: Мы говорим, что некоторое множество чисел М замкнуто относительно некоторого действия, если для всяких двух чисел их М, для которых определен результат данного действия над ним, число, является этим результатом, всегда принадлежащим М.
Пример:
1) N Множество натуральных чисел замкнуто относительно сложения, т.к. "a, bÎN => (a+b) ÎN.
В отношении умножения множество N так же замкнуто. Но оно не является замкнутым относительно вычитания и деления. Действительно:
5, 7 ÎN, но 5-7=-2 ÏN,
3, 2ÎN, но 3:2=1,5 ÏN
2) Множество целых чисел Z замкнуто относительно сложения, вычитания и умножения.
3) Множество чисел вида 2к, кÎN, замкнуто относительно умножения и деления.
2к*2l=2k+l
2к:2l=2k-l
В связи с замкнутостью действий на множестве выделились классы числовых множеств.
Рассмотрим один их классов, называемых полем.
Определение 2: Множество чисел М, содержащие не менее двух чисел, называется числовым полем, если оно замкнуто относительно действий сложения, вычитания, умножения и деления.
Последнее означает, что для любых a, b ÎM, должно иметь место a+b, a-b, a*b ÎM. Так же для любого aÎM и любого b¹0 из М, должно выполняться a:bÎM.
Пример:
Среди важнейших числовых полей наиболее важными являются:
1) поле всех рациональных чисел;
2) поле всех вещественных чисел;
3) поле всех комплексных чисел.
Что касается множества всех целых чисел, то оно не является числовым полем, ибо не замкнуто относительно деления.
Существует бесконечно много числовых полей. Нас, в данном случае интересует поле алгебраических чисел.
2.2 Определение алгебраического числа.
Существуют различные признаки, по которым их общего множества Z выделяю те или иные подмножества, подвергаемые специальному изучению. С точки зрения важного для алгебры понятия алгебраического уравнения, естественным представляется выделение классов чисел, являющихся корнями алгебраических уравнений, коэффициенты которых принадлежат тому или иному классу чисел.
Определение 3: Число Z называется алгебраическим, если оно является корнем какого-нибудь алгебраического уравнения с целыми коэффициентами:
anxn+an-1xn-1+…+a1x+a0=0
(a0, a1, … ,anÎZ; an¹0),
т.е. выполняется:
anzn+an-1zn-1+…+a1z+a0=0
Числа не являющиеся алгебраическими называются трансцендентными.
В определении алгебраического числа можно допустить, чтобы коэффициенты a0, a1, … ,an-1, an были любыми рациональными числами, поскольку, умножив левую и правую части уравнения на целое число, являющиеся общим кратным знаменателем всех коэффициентов, мы получили уравнение с целыми коэффициентами, корнем которого будет наше число.
К алгебраическим числам принадлежат, в частности, и все рациональные числа. Действительно, рациональное число z= 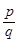 (p, qÎN) очевидно является корнем уравнения: qx-p=0.
(p, qÎN) очевидно является корнем уравнения: qx-p=0.
Также всякое значение корня любой степени из рационального числа является алгебраическим числом. Действительно, число z= 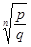 (p, qÎN) является корнем уравнения:
(p, qÎN) является корнем уравнения:
qxn-p=0.
Существуют и другие алгебраические числа, нежели указанное выше.
Пример:
1) Чиcло z= 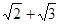 является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z2=2+2
является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z2=2+2 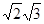 +3. Отсюда z2-5=
+3. Отсюда z2-5= 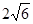 . Возводя в квадрат обе части этого равенства, получим: z4-10z2+25=24. Отсюда следует, что число z является корнем следующего уравнения:
. Возводя в квадрат обе части этого равенства, получим: z4-10z2+25=24. Отсюда следует, что число z является корнем следующего уравнения:
x4-10x2+1=0
2) Всякое число z=a+bi, у которого компоненты a и b – рациональные числа, являются алгебраическими. Докажем это.
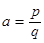 ,
, 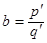 (p, q,
(p, q, 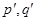 Î N).
Î N).
Из равенства 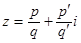 , получаем:
, получаем: 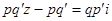 . Отсюда, возводя в квадрат, получим:
. Отсюда, возводя в квадрат, получим: 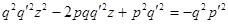 . Следовательно, я является корнем уравнения:
. Следовательно, я является корнем уравнения:
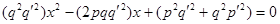
все коэффициенты которого целые числа.
В дальнейшем мы будем рассматривать только действительные алгебраические числа, не оговаривая этого каждый раз.
Из f(x)=0 следует f(z)j(x)=0, где в качестве j(x) можно взять любой многочлен с целыми коэффициентами. Таким образом для любого алгебраического числа z, из всех этих многочленов обычно рассматривают многочлен наименьшей степени.
Определение 4: Число n называется степенью алгебраического числа z, если z есть корень некоторого многочлена n-ой степени с рациональными коэффициентами и не существует тождественно не равного нулю многочлена с рациональными коэффициентами степени, меньшей чем n, корнем которого является z.
Если корень многочлена n-ой степени с целыми рациональными коэффициентами z не является корнем ни одного тождественно неравного нулю многочлена с целыми коэффициентами степени меньшей чем n, то z не может быть корнем и тождественно неравного нулю многочлена с рациональными коэффициентами степени меньшей чем n, т.е. z – алгебраическое число степени n.
Рациональные числа являются алгебраическими числами первой степени. Любая квадратическая иррациональность представляет собой алгебраическое число 2-й степени, так как, являясь корнем квадратичного уравнения с целыми коэффициентами, она не является корнем какого-либо уравнения 1-й степени с целыми коэффициентами. Алгебраические числа 3-й степени часто называют кубическими иррациональностями, а 4-й степени биквадратическими иррациональностями.
Пример:
1) 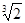 - алгебраическое число 3-й степени, т.е. кубическая иррациональность. Действительно, это число есть корень многочлена 3-й степени с целыми коэффициентами x3-2=0 и
- алгебраическое число 3-й степени, т.е. кубическая иррациональность. Действительно, это число есть корень многочлена 3-й степени с целыми коэффициентами x3-2=0 и 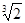 не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами.
не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами.
Определение 5: Если алгебраическое число n-й степени z является корнем многочлена f(x)=xn+b1xn-1+ … +bn (n³1) (1) с рациональными коэффициентами, то f(x) называется минимальным многочленом для z.
Таким образом, минимальным многочленом для z называется многочлен наименьшей степени с рациональными коэффициентами и старшим коэффициентом, равном единице, корнем которого является z.
Если вместо многочлена (1) взять какой-либо другой многочлен с рациональными коэффициентами степени n, корнем которого является z, то многочлен (1) может быть получен из него делением всех коэффициентов на старший член.
Пример:
1) Минимальным многочленом для 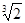 является x3-2, так как корень этого многочлена
является x3-2, так как корень этого многочлена 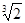 не является корнем какого-либо многочлена степени с рациональными коэффициентами.
не является корнем какого-либо многочлена степени с рациональными коэффициентами.
Теорема 1: Если f(x) минимальный многочлен алгебраического числа z и f(x) многочлен с рациональными коэффициентами, такой, что F(z)=0, то f(x) делитель F(x), т.е. F(x)=f(x)g(x), где g(x) также многочлен с рациональными коэффициентами.
Доказательство: Согласно известной теореме алгебры F(x) можно представить в виде:
F(x)=f(x)g(x)+r(x)
где g(x) и к(ч) – многочлены с рациональными коэффициентами, причем степень r(x) меньше степени f(x). Поскольку F(x)=0 и f(z)=0, то придавая x значение z, получаем r(z)=0; z – корень многочлена r(x) с рациональными коэффициентами степени, меньшей чем у минимального для z многочлена, т.е. меньшей чем степень z. Это может быть только если r(x) тождественно равен нулю, а значит F(x)=f(x)g(x). Теорема доказана.
Теорема 2: Для любого алгебраического числа z минимальный многочлен неприводим над полем рациональных чисел.
Доказательство:
Пусть f(x) – минимальный многочлен для z. Предположим, что f(x) приводим над полем рациональных чисел, т.е., что f(x)=w(x)j(x), w(x)j(x) – многочлены с рациональными коэффициентами, степени меньшей, чем n.
Из равенства w(x)j(x)=f(x)=0 следует, что из двух чисел w(x) и j(x), по крайней мере одно равно нулю. Пусть например w(x)=0, тогда z – корень тождественно не равного нулю многочлена w(x) с рациональными коэффициентами, степени меньшей, чем n, т.е. меньшей чем у f(x). А это противоречит тому, что f(x) – минимальный многочлен для z. Предположение, что f(x) приводим над полем рациональных чисел, оказалось неверным, т.е. f(x) неприводим над этим полем. Теорема доказана.
Теорема 3: Если z корень неприводимого над полем рациональных чисел многочлена F(x) с рациональными коэффициентами степени n, то z – алгебраическое число степени n.
Доказательство:
Обозначим минимальный многочлен для z через f(x). Согласно теоремы 1: F(x)=f(x)g(x); где g(x) – многочлен с рациональными коэффициентами. Поскольку F(x) неприводим над полем рациональных чисел и f(x) отлично от постоянного, то g(x)=c, где c – рационально. F(x)=cf(x), т.е. z – алгебраическое число n-й степени. Теорема доказана.
Пример:
Пусть p – простое число.
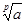 при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена.
при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена.
xp-a=0
Если z – алгебраическое число степени n и f(x) – минимальный многочлен для z, то все корни z1, z2, … zn уравнения f(x)=0, отличные от z, называют сопряженным с z.
Один из корней совпадает с z, будем ставить его на первое место, т.е. z=z1.
2.3. Поле алгебраических чисел
Теорема 4: Множество всех действительных алгебраических чисел представляет собой поле, т.е. сумма, разность, произведение и частное двух алгебраических чисел a и b (для частного при b¹0) являются алгебраическими числами.
Доказательство:
1) Пусть a - корень многочлена f(x) степени n с целыми коэффициентами, корни которого a1, a2, … ,an, a и b - корень многочлена j(x) степени m с целыми коэффициентами, корни которого b1, b2, … bm (b=b1). Рассмотрим многочлен:
F(x)= 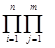 (x-(ai+bi))=
(x-(ai+bi))=
= (x-a1-b1) (x-a1-b2) … (x-a1-bm)
(x-a2-b1) (x-a2-b2) … (x-a2-bm)
- - - - - - - - - - - - - - - - - - - - - - - - - -
(x-an-b1) (x-an-b2) … (x-an-bm) (2)
Если в этом произведении сделать какую угодно подстановку величин a1, a2, … ,an, то некоторые строки переставляется местами, но произведение в целом не изменится. Это значит, что F(x) – симметрический многочлен по отношению b1, b2, … bm. В целом F(x) – симметрический многочлен от двух систем аргументов: a1, a2, … ,an и b1, b2, … bm.
Согласно известным теоремам о симметрических многочленах, коэффициенты многочлена F(x) могут быть выражены рационально через элементарные симметрические функции от a1, a2, … ,an и b1, b2, … bm, т.е. через целые коэффициенты, f(x) и j(x). Это значит, что коэффициенты F(x) рациональны, и, следовательно, число a+b=a1+b1, являющегося, как это непосредственно видно из формулы (2), корнем F(x), есть алгебраическое число.
2) Для доказательства того, что произведение двух алгебраических чисел a и b есть алгебраическое число, достаточно, аналогично тому, как это было только что сделано для многочлена (2), рассмотреть многочлен:
F(x)= 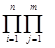 (x-aibi) (3)
(x-aibi) (3)
Этот многочлен имеет в качестве одного из своих корней a1b1=ab.
3) Пусть b - корень многочлена j(x)=b0xn+ b1xn-1+ … bn, (bi – целые числа). Тогда -b является корнем многочлена с целыми коэффициентами.
j(-x)=(-1)nb0xn+(-1)n-1b1xn-1+ … bn, а при b¹0 корень многочлена xnj( 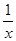 )=b0+b1x+ … bnxn. Таким образом, вместе с b алгебраическими числами являются -b и
)=b0+b1x+ … bnxn. Таким образом, вместе с b алгебраическими числами являются -b и 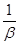 .
.
Разность может быть представлена в виде a+(-b), т.е. в виде суммы двух алгебраических чисел. При b¹0 частное 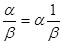 , являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число.
, являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число.
Если степени алгебраических чисел a и b равны m и n, то, взяв в качестве f(x) и j(x) соответствующие минимальные многочлены будем в (2) и (3) иметь многочлены степени mn, и ab алгебраические числа степени, не большей, чем mn. Многочлены j(x), j(-x), и xn 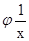 одинаковой степени, а, следовательно, b, -b,
одинаковой степени, а, следовательно, b, -b, 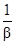 - алгебраические числа одной и той же степени, откуда следует, что и a-b и
- алгебраические числа одной и той же степени, откуда следует, что и a-b и 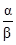 имеют степени не больше, чем mn. Теорема доказана.
имеют степени не больше, чем mn. Теорема доказана.
Пример:
1) 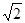 и
и 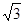 алгебраические числа 2-й степени, а
алгебраические числа 2-й степени, а 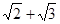 - алгебраическое число 4 степени. Действительно, если a=
- алгебраическое число 4 степени. Действительно, если a= 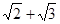 , то a2=5+
, то a2=5+ 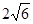 , 24-10a2+1=0, т.е. a корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x-
, 24-10a2+1=0, т.е. a корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x- 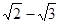 )(x-
)(x- 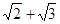 )(x+
)(x+ 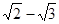 )(x+
)(x+ 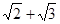 ) (4)
) (4)
Из теоремы единственности над полем рациональных чисел множители f(x) должны являться произведением каких-то множителей правой части равенства (4). Легко видеть, что из этих множителей нельзя составить многочлен с рациональными коэффициентами степени меньшей, чем 4, т.е. f(x) – неприводимый над полем рациональных чисел многочлен, а, следовательно, согласно теореме 3, 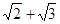 - алгебраическое число 4-й степени.
- алгебраическое число 4-й степени.
2) a= 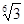 и b=
и b= 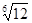 , как легко видеть, это алгебраические числа 6-й степени, а произведение ab=
, как легко видеть, это алгебраические числа 6-й степени, а произведение ab= 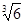 - алгебраическое число 3-й степени.
- алгебраическое число 3-й степени.
|
из
5.00
|
Обсуждение в статье: II. Поле алгебраических чисел. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

