Анализ уровня и динамики цен на лекарственные препараты. Современные методы

Орлов А.С. канд. фарм. Наук

Обоснованные управленческие решения в области ценообразования на лекарственные препараты (ЛП) невозможны без объективных сведений о ценовых изменениях на фармрынке, текущей ценовой ситуации и интенсивности ценовой конкуренции. Ценовой анализ — неотъемлемая часть маркетинговых исследований любого субъекта фармрынка. Анализ цен актуален и для госорганов, ответственных за проведение регуляторной политики на рынке ЛП.

Анализ цен проводится как для фармрынка в целом, так и в разрезе его деления на территориальные субъекты, рыночные сегменты, уровни продуктовой вертикали (рис.). В качестве объектов исследования выступают цены производителей ЛП, фармдистрибьюторов, розничных компаний. Анализ цен может проводиться в разных сегментах фармрынка — в коммерческом розничном, госпитальном, сегменте льготного лекарственного обеспечения.

Глоссарий

Уровень цен — обобщающий показатель, характеризующий состояние цен за определенный период времени, на определенной территории, по совокупности товаров и товарных видов.

Анализ цен на фармрынке заключается в изучении уровня и динамики цен на ЛП, которые характеризуют сложившуюся ценовую ситуацию и могут быть использованы для оценки интенсивности ценовой конкуренции. Для измерения уровня цен используются средние показатели, выбор которых зависит от наличия ценовой информации.

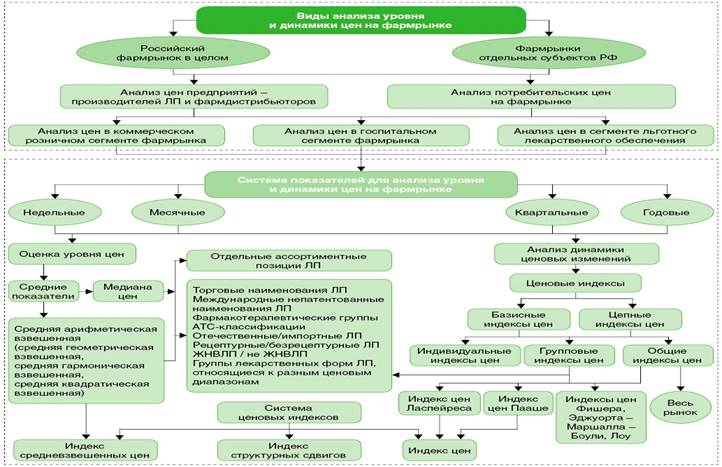
Виды анализа уровня и динамики цен на фармрынке и используемая для его проведения система показателей.

Средние цены отдельных ассортиментных позиций ЛП и среднегрупповые цены наиболее часто рассчитываются по формулам средней арифметической взвешенной (1) и (2) путем деления стоимости товара или товарной группы на соответствующий объем в натуральном выражении. В качестве товарных групп выступают отдельные торговые наименования ЛП, МНН, фармакотерапевтические группы АТС-классификации, отечественные и импортные, рецептурные и безрецептурные ЛП, препараты, включенные в Перечень ЖНВЛП и не включенные в него, а также препараты, относящиеся к разным группам лекарственных форм и различным ценовым диапазонам. Предпочтение средней арифметической взвешенной перед другими видами средних — средней геометрической, средней гармонической, средней квадратической — отдается в силу ее простоты, ясного экономического смысла и ряда положительных математических свойств, облегчающих расчет.

где: P_i — средневзвешенная розничная цена i-й ассортиментной позиции ЛП, руб.;

P_ij — розничная цена i-й ассортиментной позиции ЛП в j-й аптечной организации, руб.;

Q_ij — суммарный объем продаж i-й ассортиментной позиции ЛП в j-й аптечной организации в натуральном выражении;

n — общее количество исследуемых аптечных организаций;

P — средневзвешенная розничная цена товарной группы ЛП, руб.;

Q_i — суммарный объем продаж i-й ассортиментной позиции ЛП во всех исследуемых аптечных организациях;

m — число ассортиментных позиций ЛП в товарной группе.

Средние цены используются самостоятельно и в качестве промежуточного этапа изучения динамики цен в различных статистических методах, в т. ч. в расчетах индексов. Во многих странах средние цены широко применяются государственными контролирующими органами для определения предельного уровня регулируемых цен на ЛП, для расчета референтных цен. Средние показатели используются различными субъектами фармрынка при формировании цен на собственную продукцию, для анализа цен и ценовой политики конкурентов. Кроме того, средние цены применяются в независимых аналитических исследованиях фармрынка для сравнительного ценового анализа ЛП, для оценки ценовых различий между определенными товарными группами медикаментов, для региональных сопоставлений уровней цен на ЛП [4, 6].

Помимо средних цен для характеристики уровня цен может использоваться медиана цен, которая относится к особому виду средних величин — структурным средним. Расчет медианы (3) особенно актуален при отсутствии достаточной ценовой информации, например в случаях, когда неизвестны крайние границы ценовых интервалов.

где: P_Me — медиана цен;

P₀ — нижняя граница медианного интервала;

p — величина медианного интервала цен;

S_Me—1 — накопленная частота интервала цен, предшествующего медианному;

f_Me — частота медианного интервала цен.

Расчет средних цен имеет смысл только для групп однородных товаров, которые должны иметь соизмеримую единицу для выражения их количества по видам. В этой связи анализ цен на фармрынке на основе средних показателей сопряжен с методологическими трудностями, поскольку из-за многообразия доз и форм выпуска, а следовательно, и единиц физического измерения возможности образования группировок товаров в натуральном выражении ограниченны. Кроме того, на уровень средних цен помимо ценовых факторов оказывают влияние и структурные сдвиги, связанные с ассортиментом. Это приводит к тому, что динамика средних цен не может рассматриваться в качестве индикатора ценовой динамики в чистом виде.

Для изучения динамики цен на фармрынке наиболее широко применяется индексный метод, основанный на построении и расчете ценовых индексов. Под индексом цен понимается относительный показатель, характеризующий изменение во времени или соотношение в пространстве цен какого-либо товара, отдельной товарной группы или всей их совокупности [1–3]. Индексы цен — важная обобщающая характеристика фармрынка. С помощью индексов можно:

· изучать динамику уровня цен для отдельных ассортиментных позиций ЛП за 2 и более периодов времени;

· оценивать динамику цен для товарных групп ЛП и для фармацевтического рынка в целом;

· анализировать степень влияния структурных изменений в потреблении ЛП на динамику цен на фармацевтическом рынке и определять направление вектора смещения потребительского спроса в сторону более дорогих или более дешевых лекарств;

· устанавливать степень интенсивности ценовой конкуренции в различных сегментах фармацевтического рынка;

· осуществлять перерасчет значений различных экономических показателей из фактических в сопоставимые.

В практике ценового анализа используется множество разнообразных индексов цен, которые могут быть классифицированы по нескольким признакам. По периоду исчисления индексы цен, как и средние показатели, подразделяются на недельные, месячные, квартальные, годовые. В зависимости от используемой базы сравнения индексы цен могут быть разделены на базисные и цепные. Базисные индексы цен рассчитываются с постоянной базой сравнения и определяются на основе сравнения цен в текущем и базисном периодах. Цепные индексы цен характеризуются переменной базой сравнения, поскольку рассчитываются путем сопоставления цен в текущем и предшествующем периодах. По степени охвата исследуемых ЛП различают индивидуальные, групповые и общие индексы цен. Индивидуальные индексы цен характеризуют изменение цен отдельных ассортиментных позиций ЛП. Групповые индексы цен отражают ценовые изменения для отдельных групп товаров. Общие индексы цен на фармрынке рассчитываются для изучения динамики цен всей совокупности ЛП [1–3].

Для расчета групповых и общих индексов цен применяются различные формулы, среди которых в международной и отечественной практике ценового анализа наибольшее применение находит индекс цен Ласпейреса, что обусловлено его простотой, наглядностью, четкостью интерпретации и удобством расчета [1, 2, 4, 9]. Индекс цен Ласпейреса с базисными фиксированными величинами чаще всего определяется по среднеарифметической взвешенной формуле (4), преимущество которой в том, что она позволяет легко производить расчет индекса и облегчает последующие перерасчеты.

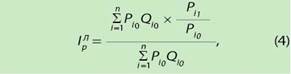
где: I^p_Л — индекс цен Ласпейреса, определенный по среднеарифметической взвешенной формуле;

P_i1 — цена товара (услуги) в отчетном периоде;

P_i0 — цена товара (услуги) в базисном периоде;

P_i0Q_i0 — расходы на приобретение товара (услуги) в общих потребительских расходах населения базисного периода.

При исчислении индекса цен по формуле Ласпейреса веса фиксируются на уровне базисного периода и остаются неизменными в течение некоторого промежутка времени, поэтому индекс способствует измерению динамики стоимости базисного (неизменного) объема продукции. Ясный экономический смысл и технологичность, обусловленная возможностью использовать в расчетах весов базисного периода, сделали популярной среднеарифметическую взвешенную формулу Ласпейреса при проведении различных ценовых исследований, в т. ч. исследований динамики цен на фармрынке [9].

Использование индекса Ласпейреса с фиксированными весами базового периода особенно актуально при проведении оперативного анализа, поэтому он применяется для определения индекса потребительских цен, индекса цен промышленного производства и их фармацевтических составляющих, расчетом которых занимаются национальные статистические ведомства. Индекс цен Ласпейреса применяется для изучения динамики цен на фармрынке, дифференцированного ценового анализа в разрезе агрегированных товарных групп ЛП и ценовых диапазонов, для сравнительного анализа уровней цен между разными регионами и странами, для оценки результативности и эффективности мер государственного регулирования, для анализа расходов населения на медикаменты, для изучения влияния инфляционных процессов на уровень цен на ЛП, для сравнения темпов роста цен на ЛП с темпами роста цен на другие группы товаров [5, 7, 8].

Индекс Ласпейреса всегда имеет определенную степень условности. Это связано прежде всего с тем, что при его расчете учитываются изменения цен не по всей совокупности продукции, а только по выбранным товарам-представителям, которые составляют так называемый потребительский набор [9]. По мере отдаления от базисного года потребительский набор по видам, количеству, качеству вошедших в него товаров-представителей все менее соответствует структуре и составу объема продукции текущего периода. Поэтому состав потребительского набора, а следовательно, и система весов должны периодически пересматриваться. Применение индекса цен Ласпейреса требует также решения ряда других важных вопросов, касающихся выбора базисного года для постоянных весов, определения срока использования весовых коэффициентов без их пересмотра, увязки индексов, рассчитанных по новым весам, с ранее существующими динамическими рядами индексов цен.

В отличие от индекса цен Ласпейреса текуще-взвешенный индекс цен Пааше предполагает пересчет весов, обновляемых от периода к периоду, что требует больших затрат времени, финансовых и трудовых ресурсов, поэтому его сложно использовать для регулярной обработки ценовой информации. Тем не менее индекс Пааше в среднегеометрической форме (5) используется для определения дефлятора валового национального продукта, для анализа динамики цен в торговле, сельскохозяйственном секторе, т. е. в случаях, когда требуется расчет, максимально приближенный к совокупности товаров, произведенных в отчетном периоде.

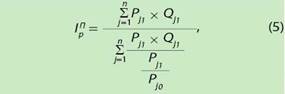
где: I^p_П — индекс цен Пааше, определенный по средней гармонической формуле;

P_j1 — цена товара (услуги) в отчетном периоде;

P_j0 — цена товара (услуги) в базисном периоде;

P_j1 x Q_j1 — расходы на приобретение товара (услуги) в общих потребительских расходах населения текущего периода.

Использование индекса Пааше, в отличие от индекса Ласпейреса, наиболее целесообразно в случае значительных структурных изменений, требующих применения подвижной системы весов.

Между индексами Пааше и Ласпейреса существует функциональная зависимость (6), из которой следует, что вследствие отрицательной корреляции цены и проданного количества товара, а также всегда положительных коэффициентов вариации значения индекса Пааше обычно меньше значений индекса Ласпейреса (эффект Гершенкрона). Статистическим анализом доказано, что в долговременном аспекте индекс Ласпейреса завышает рост цен, тогда как индекс Пааше его занижает, причем в случае международных сопоставлений разница между индексами, взвешенными разными способами, может составлять несколько процентов [1–3].

где r_{ip, iq} — коэффициент корреляции между индивидуальными индексами физического объема и цен на отдельные виды продукции;

V_iq — коэффициент вариации индивидуальных индексов физического объема продукции;

V_ip — коэффициент вариации индивидуальных индексов цен.

В связи с расхождениями в результатах между индексами цен с текущими и базисными весами некоторые исследователи полагают, что их использование ведет к отклонениям в величине индекса от его истинного значения, в первом случае в сторону понижения, а во втором — повышения. Однако при таком подходе рассматривается не экономическое содержание индексов цен, а определенные формальные требования к ним. С позиции экономического содержания одинаково правомерны индексы цен с использованием и базисных, и текущих весов. Расхождения между их величинами не являются результатом противоположных отклонений от единственно правильной величины. Правомерен и более высокий результат, полученный на основе формулы Ласпейреса, и более низкий результат, полученный по формуле Пааше, т. к. в обоих случаях измеряются два различных экономических явления: в первом — изменение цен товаров по структуре базисного, а во втором — текущего периода. Экономическое содержание обоих индексов различно, поэтому их величины также должны отличаться [9].

Тем не менее ряд аналитиков использует в своих исследованиях формы индексов цен, «очищенные» от возможных отклонений.

Эффект Гершенкрона наблюдается только при отрицательной зависимости между количеством реализованной продукции и ценами и проявляется тогда, когда с ростом цен происходит снижение объемов реализации.

В связи со значительными расхождениями между результатами расчетов индексов Ласпейреса и Пааше некоторые исследователи считают их недостаточно объективными средствами анализа цен и предлагают использовать альтернативные формулы индексов, которые могли бы дать результаты, свободные от влияния весов различных периодов. Среди предлагаемых альтернативных показателей наиболее часто упоминаются индексы Фишера, Эджуорта — Маршалла — Боули, Лоу [1–3, 9].

Индекс Фишера вычисляется как средняя геометрическая от произведения индексов цен Ласпейреса и Пааше (7).

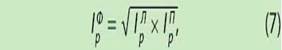
где I^p_Ф — индекс цен Фишера;

I^p_Л — индекс цен Ласпейреса;

I^p_П — индекс цен Пааше.

Расчетная формула индекса Фишера получила название идеальной формулы, поскольку в ней не отдается предпочтение ни продукции базисного периода, ни продукции текущего периода [3]. Кроме того, индекс Фишера обратим во времени, т. к. при перестановке базисного и отчетного периодов получается «обратный» индекс, т. е. величина, обратная величине первоначального индекса. При этом перемножение «обратных» индексов дает единицу, как и в случае любого индивидуального индекса, каждый из которых также удовлетворяет этому условию. В этой связи многие исследователи и статистики полагают, что идеальный индекс Фишера полностью «очищен» от противоположных отклонений, свойственных другим формулам, и поэтому представляет собой точный и качественный индекс [2].

Однако принципиальный недостаток формулы индекса цен Фишера в том, что она лишена конкретного экономического содержания. Так, в отличие от агрегатных индексов цен Ласпейреса и Пааше разность между числителем и знаменателем не показывает реальной экономии (или потерь) вследствие изменения цен. Кроме того, считается, что индекс Фишера чересчур формален и далек от реальных потребностей, возникающих в процессе практических расчетов индексов цен. Поэтому на практике формула индекса цен Фишера используется редко. Чаще всего эта формула применяется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, а также в случае значительных изменений структуры весов, приводящих к существенным расхождениям в результатах расчета индексов цен по формулам Ласпейреса и Пааше. В этой связи индекс Фишера часто применяется при расчете индексов импортных и экспортных цен, а также при проведении территориальных сопоставлений. Необходимо отметить, что использование формулы Фишера при расчете территориальных индексов цен обеспечивает однозначный результат и позволяет получить индексы, которые удовлетворяют требованиям характерности весов, обратимости во времени, а также факторной пробы.

В формуле Эджуорта — Маршалла — Боули (8) в качестве весов используются средние количества проданной продукции за базисный и текущий периоды:

где I_p^Э — индекс цен Эджуорта — Маршалла — Боули;

Pi1 — цена товара (услуги) в отчетном периоде;

P_i0 — цена товара (услуги) в базисном периоде;

(Q_i1+ Q_i0) /2 - средние количества проданной продукции за базисный и текущий периоды.

По мнению зарубежных статистиков, эта формула позволяет получать результаты, лишенные отклонений, свойственных индексам Ласпейреса и Пааше. В отличие от этих ценовых индексов, которые отражают изменение цен в связи с одной из двух конкретных структур (базисного или текущего периодов), формула Эджуорта — Маршалла — Боули привязывает изменение цен к условной структуре товаров, полученной на основе усреднения текущих и базисных весов. Кроме того, этот индекс учитывает сдвиги в структуре продаж, связанные с ассортиментом. В то же время условная структура товарооборота, используемая при расчете индекса, не характерна ни для одного реального периода и потому не имеет прямого экономического смысла.

Следует отметить, что индекс Эджуорта — Маршалла — Боули — частный случай индекса Лоу, в котором в качестве весов используются средние количества реализованной продукции за несколько (два и более) периодов (9).

где I_p^Лоу — индекс цен Лоу;

P_i1 — цена товара (услуги) в отчетном периоде;

P_i0 — цена товара (услуги) в базисном периоде;

Q_i — среднее количество проданной продукции за анализируемый период.

Индекс цен Лоу главным образом применяется в фундаментальных исследованиях по изучению ценовой динамики в течение продолжительных периодов времени (5–10 лет). Этот индекс дает возможность анализировать цены с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе продукции [3].

Помимо вышеперечисленных ценовых индексов для анализа динамики цен на фармацевтическом рынке также могут использоваться индексы, рассчитываемые по формулам Торнквиста, Гири — Камиса, Уолша, Герарди, однако в силу формального характера, а также сложностей расчета и экономической интерпретации все они применяются крайне редко [3].

Для обобщения вышесказанного в таблице приведена сравнительная характеристика наиболее широко используемых в ценовых исследованиях фармацевтического рынка индексов цен.

При изучении динамики цен на фармрынке необходимо учитывать, что они могут отражать изменение не только собственно цен, но и долей продаж отдельных ассортиментных позиций ЛП. Поэтому индекс средневзвешенных цен (ИСВЦ) характеризует как изменение цен, так и структуры продаж. В то же время индексы цен Ласпейреса и Пааше (ИЦ) показывают изменение исключительно индексируемой величины — цены. Связь между индексом средневзвешенных цен и индексами цен (10) устанавливается с помощью индекса структурных сдвигов (ИСС), который отражает влияние изменения структуры продаж на динамику средневзвешенных цен:

Таким образом, для анализа уровня и динамики цен на фармацевтическом рынке могут быть использованы разнообразные статистические показатели. В настоящее время в практике анализа цен на фармацевтическом рынке среди различных методов изучения ценовой динамики предпочтение отдается индексному методу в силу его технологичности, простоты, а также широких возможностей использования для проведения аналитических исследований. Среди всех известных формул ценовых индексов и в зарубежной, и в отечественной статистике (в частности, при расчете ИПЦ) наибольшее применение получила формула Ласпейреса, поскольку она проста и удобна при проведении оперативных расчетов. Вместе с тем применение индекса цен Ласпейреса, не требующего обновления весов при сдвиге текущего периода и отвечающего требованиям технологичности и наглядности, адекватно только в случае небольших изменений в структуре продаж. При значительных структурных изменениях (существенное превышение индексом Ласпейреса индекса Пааше) появляется ярко выраженная зависимость результатов анализа ценовой динамики от используемой формулы, т. е. неоднозначность оценок, вследствие чего требования к выбору расчетной формулы индекса цен резко повышаются, и она уже не может выбираться исходя лишь из требования технологичности. В таких ситуациях более целесообразно использование индексов Паше, Фишера, Эджуорта — Маршалла — Боули или Лоу. Однако при этом необходимо иметь в виду, что с изменением весовой структуры индекса цен изменяется не только численный результат анализа, но и его экономическое содержание. Безусловно, в целом ряде случаев выбор расчетной формулы для ценового индекса может оказаться вынужденным, например, в связи с ограниченным количеством ценовой информации или необходимостью получения оперативных результатов анализа динамики цен на ЛП. Однако основополагающий подход к решению этого важного вопроса должен состоять в том, что при выборе формулы индекса цен следует руководствоваться исключительно экономическими соображениями, определяемыми целями и задачами, которые стоят перед каждым конкретным исследованием.

Таблица