Правила построения сетевых графиков

Курсовое проектирование

Метод кратчайшего пути

 

Введение

 

Теория графов - раздел дискретной математики, изучающий свойства графов. Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т.п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т.п. - как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Если изобразить сеть дорог, связывающую некоторые города, линиями, а города - точками, то получается определенная схема. Такая же схема возникает, если изобразить систему электрических соединений, сетку телеграфных связей и т.п. Если составить план большой работы, то можно изобразить этапы работы точками, а последовательность - какой этап следует за каким - линиями со стрелками, соединяющими эти точки.

Математическая теория организации на базе теории графов исследует свойства коллективов и групп.

Предметом курсовой работы являются графы, с помощью которых могут быть описаны многие структуры, представляющий практический интерес в математике и информатике.

Целями работы являются изучение основных понятий теории графов и разработка программного обеспечения для решения задач поиска кратчайшего пути между вершинами графа.

 

Понятия теории графов

 

Графом называется фигура, состоящая из точек (вершин) и линий (ребер).

Объекты представляются как вершины, или узлы графа, а связи - как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Граф, или неориентированный граф - это упорядоченная пара, для которой выполнены следующие условия:

V это непустое множество вершин или узлов;

E это множество пар (в случае неориентированного графа - неупорядоченных) вершин, называемых рёбрами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств. Вершины и рёбра графа называются также элементами графа, число вершин в графе - порядком, число рёбер - размером графа. Вершины и называются концевыми вершинами (или просто концами) ребра. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают, то есть. Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

При изображении графов на рисунках чаще всего используется система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов). Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Различают планарные и непланарные графы.

Планарный граф - это граф, который можно изобразить на рисунке без пересечения рёбер (простейшие - треугольник или пара связанных вершин), иначе - непланарный. В том случае, если граф не содержит циклов (путей однократного обхода рёбер и вершин с возвратом в исходную вершину), его принято называть «деревом». Важные виды деревьев в теории графов - бинарные деревья, где каждая вершина имеет одно входящее ребро и ровно два выходящих, или является конечной - не имеющей выходящих рёбер.

Изображение графа может не совпадать с собственно графом (абстрактной структурой), так как одному графу можно сопоставить не одно графическое представление. Изображение призвано показать, какие пары вершин соединены рёбрами, а какие - нет. На практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

 

Основные понятия

Сетевая модель

алгоритм сетевой неопределенность дейкстра

Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-компьютерная модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет:

во-первых, более четко выявить взаимосвязи этапов реализации проекта;

во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ.

В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управления (СПУ). Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающих определенными ресурсами и выполняющих определенный комплекс операций, который призван обеспечить достижение намеченной цели, например, разработку нового изделия, строительства объекта и т.п.

Основой сетевого планирования и управления является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.

Основные понятия сетевой модели:

.   событие,

.   работа,

.   путь

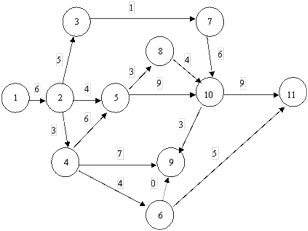
На рис 1 графически представлена сетевая модель, состоящая из 11 событий и 16 работ, продолжительность выполнения которых указана над работами.

Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i, j), где i - номер события, из которого работа выходит, а j - номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность t (i, j). Например, запись t (2,5) = 4 означает, что работа (2,5) имеет продолжительность 4 единицы.

К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой; такие работы называются фиктивными и на графике изображаются пунктирными стрелками.

Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении сетевая модель изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер (i = 1, 2,…, n).

В сетевой модели имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.

Путь - это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной выше модели путями являются L₁ = (1, 2, 3, 7, 10, 11), L₂ = (1, 2, 4, 6, 11) и др.

Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают L_Kp, а его продолжительность - t_кр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.етевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.

 

Правила построения сетевых графиков

 

1. Завершающее событие лишь одно

.   Исходное событие лишь одно

.   Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Если два события связаны более чем одной работой, рекомендуется найти дополнительное событие и фиктивную работу

.   В сети не должно быть замкнутых циклов.

.   Если для выполнения одной из работ необходимо получить результаты всех работ, входящих в предшествующее для нее событие, а для другой работы достаточно получить результат нескольких из этих работ, то нужно ввести дополнительное событие, отражающее результат только этих последних работ, и фиктивную работу, связывающую новое событие с прежним.

 

Рис. 2. Примеры построения событий в графах

 

Перед расчетом СМ следует убедиться, что она удовлетворяет следующим основным требованиям:

. События правильно пронумерованы, т.е. для каждой работы (i, j) i <j (см. на рис. 3. работы (4,3) и (3,2)). При невыполнении этого требования необходимо использовать алгоритм пере нумерации событий, который заключается в следующем:

нумерация событий начинается с исходного события, которому присваивается №1;

из исходного события вычеркивают все исходящие из него работы (стрелки), и на оставшейся сети находят событие, в которое не входит ни одна работа, ему и присваивают №2;

затем вычеркивают работы, выходящие из события №2, и вновь находят событие, в которое не входит ни одна работа, и ему присваивают №3, и так продолжается до завершающего события, номер которого должен быть равен количеству событий в сетевом графике;

если при очередном вычеркивании работ одновременно несколько событий не имеют входящих в них работ, то их нумеруют очередными номерами в произвольном порядке.

. Отсутствуют тупиковые события (кроме завершающего), т.е. такие, за которыми не следует хотя бы одна работа (событие 5 из рис. 3);

. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа (событие 7);

. Отсутствуют циклы, т.е. замкнутые пути, соединяющие событие с ним же самим (см. путь (2,4,3)).

 

Рис. 3. При невыполнении указанных требований бессмысленно приступать к вычислениям характеристик событий, работ и критического пути.

Для событий рассчитывают три характеристики: ранний и поздний срок совершения события, а также его резерв.

Ранний срок свершения события определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события, причем t_р(1)=0, a t_р(N)=t_Kp(L):

 

t_р(j)=max{t_р(j)+(i, j)}; j=2,…, N

 

Поздний срок свершения события характеризует самый поздний допустимый срок, к которому должно совершиться событие, не вызывая при этом срыва срока свершения конечного события:

 

t_n(i)=min{t_n(i) - t (i, j)}; j=2,…, N-1

Этот показатель определяется «обратным ходом», начиная с завершающего события, с учетом соотношения t_n(N)=t_p(N).

Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i):

(i)=t_n(i) - t_p(i)

 

Резерв показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ. Для всех работ (i, j) на основе ранних и поздних сроков свершения всех событий можно определить показатели:

 

Ранний срок начала - t_pn(i, j)=p(i);

Ранний срок окончания - t_po(i, j)=t_p(i)+t (i, j);

Поздний срок окончания - t_no(U)=t_n(j);

Поздний срок начала - t_пн(i, j)=t_n(j) - t (i, j);

Полный резерв времени - R_n(i, j)=t_n(j) - t_p(i) - t (i, j);

Независимый резерв -

R_н(i, j)=max {0; t_p(j) - t_n(i) - t (i, j)}=max {0; R_n(i, j) - R(i) - R(j)}.

 

Полный резерв времени показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится.

Независимый резерв времени соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие - начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.

Путь характеризуется двумя показателями - продолжительностью и резервом. Продолжительность пути определяется суммой продолжительностей составляющих его работ.

Резерв определяется как разность между длинами критического и рассматриваемого путей. Из этого определения следует, что работы, лежащие на критическом пути, и сам критический путь имеют нулевой резерв времени. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности общего срока выполнения всех работ.

Перечисленные характеристики СМ могут быть получены на основе приведенных аналитических формул, а процесс вычислений отображен непосредственно на графике или в матрице (размерности N*N), или в таблице.

3. Сетевое планирование

 

Сетевой анализ (сетевое планирование) - метод анализа сроков (ранних и поздних) начала и окончания нереализованных частей проекта, позволяет увязать выполнение различных работ и процессов во времени, получив прогноз общей продолжительности реализации всего проекта.

Для проведения сетевого планирования вначале необходимо расчленить проект на ряд отдельных работ и составить логическую схему (сетевой граф).

Работа - это любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени и приводящие к определенным результатам.

Событие - это факт окончания всех входящих в него работ. Считается, что оно происходит мгновенно. С исходного события, которое не имеет предшествующих работ, начинается выполнение проекта. Завершающим событием, которое не имеет последующих работ, заканчивается выполнение проекта.

После построения сетевого графа необходимо оценить продолжительность выполнения каждой работы и выделить работы, которые определяют завершение проекта в целом. Нужно оценить потребность каждой работы в ресурсах и пересмотреть план с учетом обеспечения ресурсами.

 

3.1 Сетевое планирование в условиях неопределенности

 

Продолжительность выполнения работ часто трудно задать точно и потому в практической работе вместо одного числа (детерминированная оценка) задаются две оценки - минимальная и максимальная.

Минимальная (оптимистическая) оценка t_min(i, j) характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная (пессимистическая) t_mах(i, j) - при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение toж оценивается по формуле (при бета-распределении плотности вероятности):

 

t_ож(i, j)=(3t_min (i, j)+2t_max(i, j))/5.

 

Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии S²:

 

S²(i, j)=(t_max(i, j) - t_min(i, j))²/5²=0,04 (t_max(i, j) - t_min(i, j))²

 

На основе этих оценок можно рассчитать все характеристики СМ, однако они будут иметь иную природу, будут выступать как средние характеристики. При достаточно большом количестве работ можно утверждать (а при малом - лишь предполагать), что общая продолжительность любого, в том числе и критического, пути имеет нормальный закон распределения со средним значением, равным сумме средних значений продолжительности составляющих его работ, и дисперсией, равной сумме дисперсий этих же работ.

Кроме обычных характеристик СМ, при вероятностном задании продолжительности работ можно решить две дополнительные задачи:

) определить вероятность того, что продолжительность критического пути t_кр не превысит заданного директивного уровня Т;

) определить максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности р.

Первая задача решается на основе интеграла вероятностей Лапласа Ф(z) использованием формулы:

P(t_kp<T)=0,5+0,5Ф(z),

 

Где нормированное отклонение случайной величины:

=(Т-t_Kp)/S_Kp;

_Kp - среднее квадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.

При достаточно большой полученной величине вероятности (более 0,8) можно с высокой степенью уверенности предполагать своевременность выполнения всего комплекса работ.

Для решения второй задачи используется формула:

 

Т=t_ож(L_kp)+z×S_kp