 |
Главная |
Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.
|
из
5.00
|
В 1956 году отечественным математиком А.А. Марковым было предложено новое уточнение понятия алгоритма, которое позднее было названо его именем.
В этом уточнении выделенные нами 7 параметров были определены следующим образом:
Совокупность исходных данных - слова в алфавите S;
Совокупность возможных результатов - слова в алфавите W;
Совокупность возможных промежуточных результатов - слова в алфавите
Р=S 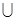 W
W 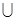 V, где V - алфавит служебных вспомогательных символов.
V, где V - алфавит служебных вспомогательных символов.
Действия:
Действия имеют вид либо a®g, либо a a g, где a, g ÎP*, где
P* - множество слов над алфавитом Р, и называется правилом подстановки. Смысл этого правила состоит в том, что обрабатываемое слово w просматривается слева направо и ищется вхождение в него слова a.
Определение.3.1. Слово a называется вхождением в слово w, если существуют такие слова b и n над тем же алфавитом, что и a и w, для которых верно: w=ban.
Если вхождение a в w найдено, то слово a заменяется на слово g.
Все правила постановки упорядочиваются. Сначала ищется вхождение для первого правила подстановки. Если оно найдено, то происходит подстановка и преобразуемое слово опять просматривается слева направо в поисках вхождения. Если вхождение для первого правила не найдено, то ищется вхождение для второго правила и т.д. Если вхождение найдено для i-го правила подстановки, то происходит подстановка, и просмотр правил начинается с первого, а слово просматривается сначала и слева направо.
Вся совокупность правил подстановки называется схемой алгоритма.
Правило начала - просмотр правил всегда начинается с первого.
Правило окончания - выполнение алгоритма заканчивается, если:
было применено правило подстановки вида a a g,
не применимо ни одно правило подстановки из схемы алгоритма.
7. Правило размещения результата - слово, полученное после окончания выполнения алгоритма.
Рассмотрим пример 1 из лекции 2:
построить алгоритм для вычисления
U(n)=n+1;
S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.
Cхема этого НАМ показана на рисунке 3.1.
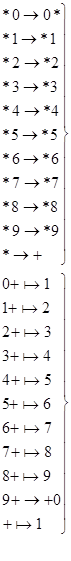
| Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов. Увеличиваем на единицу, начиная с цифр младших разрядов. |

| Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове. |
Рис.3.1. Схема НАМ для вычисления U1(n)=n+1
Нетрудно сообразить, что сложность этого алгоритма, выраженная в количестве выполненных правил подстановки, будет равна:
(k+1)+(l+1),
где k - количество цифр в n, l - количество 9, которые были увеличены на 1.
Но в любом случае сложность НАМ для U1(n) больше сложности Машины Тьюринга для этой же функции, которая равнялась k+1.
Обратите внимание, что у НАМ порядок следования правил подстановки в схеме алгоритма существенно влияет на результат, в то время как для МТ он не существеннен.
Построим НАМ для примера 2 из лекции 2:
построить алгоритм для вычисления
U2((n)1)=(n-1)1
Итак, S={|}; W=S; V=Æ, т.е. пусто.
| a
Cложность этого алгоритма равна 1, в то время как сложность алгоритма для Машины Тьюринга равнялась n.
Теперь построим НАМ для примера 3 из лекции 2:
построить алгоритм для вычисления
U3((n)1)=(n)10
S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ
Схема этого алгоритма приведена на рисунке 3.2.
| 1|®2 2|®3 3|®4 4|®5 5|®6 6|®7 7|®8 8|®9 9|®|0 |0®10 0|®1 |®0| |
Рис. 3.2. Схема НАМ для вычисления U3((n)1)=(n)10.
Сложность этого НАМ будет n+[log10n], что существенно меньше сложности для Машины Тьюринга, вычисляющей эту функцию, которая равнялась n2+[log10n(log10n+1)].
Реализацию функции U4 сравнения двух целых чисел оставляем читателю в качестве упражнения.
Замечание: исходное слово надо задать в форме 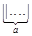 *
* 
Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга.
Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий.
Построение алгоритмов из алгоритмов.
До сих пор, строя ту или иную МТ, или НАМ мы каждый раз все делали заново. Естественно задать вопрос, а нельзя ли при построении, например, новой МТ пользоваться уже построенной ранее МТ.
Например, МТ3 из примера 3
U3((n)1)=(n)10
по существу есть надлежащим образом объединенные МТ для U1(n)=n+1 и U2((n)1)=(n-1)1.
Аналогичный вопрос можно сформулировать для НАМ. Другими словами можно ли аккумулировать знания в форме алгоритмов так, чтобы из них можно было строить другие алгоритмы.
Мы рассмотрим эту проблему применительно к МТ. Однако все сформулированные нами утверждения будут справедливы и для НАМ и для других эквивалентных уточнений понятия алгоритма. Эквивалентость уточнений понятия алгоритма мы рассмотрим позже.
Определение.3.2. Будем говорить, что МТ1 можно эффективно построить из МТ2 и МТ3 если существует алгоритм, который позволяет, имея программу для МТ2 и МТ3, построить программу для МТ3.
Определение.3.3.Последовательной композицией МТ А и В называется такая МТ С, что
область применимости МТ А и С совпадают;
C(a)=B(A(a)).
Другими словами, применение С к слову a дает такой же результат, как последовательное применение к этому же слову сначала А, а потом к результату применения А - В.
Последовательную композицию МТА и МТВ будем обозначать АoВ.
Теорема 3.1. Пусть даны МТ А и В, такие, что В применима к результатам работы А и QA 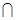 QB=Æ.
QB=Æ.
Тогда можно эффективно построить МТ С такую, что С= АoВ.
Доказательство.
В качестве алфавита данных и множества состояний для МТС возьмем объединение алфавитов данных и множеств состояний для А и В, т.е.
DC=DA 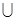 DВ, QC= QA
DВ, QC= QA 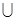 QB
QB
В программе для А все правила ap®b!w, где a,bÎDA*, wÎ{Л, П, Н} заменим на ap®bqoBw, где qoBÎ QB - начальное состояние для В. Это обеспечит включение В в тот момент, когда А свою работу закончила и не раньше, т.к. QA 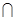 QB=Æ.
QB=Æ.
Что и т.д.
Табличная запись программы для С показана на рисунке 3.3.
 |
Рис 3.3 Структура табличной записи программ для Машины С.
Определение3.4. Параллельной композицией Машин Тьюринга А и В назовем такую Машину С, для которой:
DC=DA  DB
DB
QC=QA  QB
QB
C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).
Из этого определения видно, что порядок применения МТА и МТВ не влияет на результат. Он будет такой же как если бы мы независимо применили А к слову a, а В к слову b.
Теорема 3.2 Для любых МТ А и МТ В можно эффективно построить МТ С такую, что С=А||В
Обоснование. Мы не будем давать здесь строго доказательства в виду его технической сложности. Покажем лишь обоснование правильности утверждения теоремы. Обозначим DC=DA  DB; QC=QA
DB; QC=QA  QB.
QB.
Основная проблема: как гарантировать чтобы А не затронула слово b , а В - слово a . Для этого введем в алфавит DС символ ||. Добавим для всех состояний qiÎQC таких, что qiÎQA правила вида ||qi®||qiЛ, т.е. каретка машины А будет, натыкаясь на символ ||, уходить влево. Соответственно для всех qjÎQC таких, что qjÎQB добавим правила вида ||qj®||qjП, т.е. каретка машины В будет уходить вправо. Тем самым мы как бы ограничиваем ленту для А справа, а для В слева.
Существенным здесь является вопрос: не окажутся ли вычислительные возможности Машины Тьюринга с полулентой слабее, чем вычислительные возможности Машины Тьюринга с полной лентой?
Оказывается справедливо следующее утверждение: множество алгоритмов, реализуемых МТ с полулентой, эквивалентно множеству алгоритмов, реализуемых МТ с полной лентой. Обозначим Ф(Р) Машину Тьюринга, реализующую распознающий алгоритм:

Теорема 3.3. Для любых Машин Тьюринга А, В и Ф, имеющих один и тот же алфавит S, может быть эффективно построена машина С над тем же алфавитом S, такая что

Доказательство.
Обозначим: E(Р) тождественную машину, т.е. Е(Р)=Р
СOPY(Р) копирующую машину, т.е. СOPY(Р)=Р||Р,
где ||ÏS.
BRANCH(P) - эта машина переходит либо в состояние р1, либо в состоянии ро. Ее программа состоит из 4-х команд:
1qo®1р1П
||р1®||р1П
0qo®0роП
||ро®||роП
Построим машину

Эта машина строится по следующей формуле:
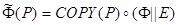
Согласно теоремам 3.1 и 3.2., мы можем построить машину  , зная Е, Ф и COPY. Теперь, имея
, зная Е, Ф и COPY. Теперь, имея  , BRNCH, A и В, можно построить машину С следующим образом:
, BRNCH, A и В, можно построить машину С следующим образом:
Машина  o BRANCH заканчивает свою работу либо в состоянии р1, если слово P обладает нужным свойством, либо в состоянии ро, находясь в начале слова P. Поэтому, если принять у машины А состояние р1, как начальное, а у машины В состояние ро, как начальное, то машина А будет включена при условии, что Ф(Р)=1, а машина В будет включена, если Ф(Р)=0.
o BRANCH заканчивает свою работу либо в состоянии р1, если слово P обладает нужным свойством, либо в состоянии ро, находясь в начале слова P. Поэтому, если принять у машины А состояние р1, как начальное, а у машины В состояние ро, как начальное, то машина А будет включена при условии, что Ф(Р)=1, а машина В будет включена, если Ф(Р)=0.
Правило композиции, определяемое этой теоремой будем записывать, если Ф то А иначе В.
Теорема 3.4. Для любых машин А и Ф можно эффективно построить машину L такую, что
L(P)={ Пока Ф(Р)=1, применяй А }
Доказательство: Заменим в доказательстве теоремы 3.3. машину В машиной Е, а заключительное состояние в машине В заменим на начальное состояние в машине 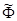 . В итоге получим нужный результат.
. В итоге получим нужный результат.
Теорема 3.5. (Бомм, Джакопини, 1962)
Любая Машина Тьюринга может быть построена с помощью операции композиций o, || , если Ф, то А иначе В, пока Ф применяй А.
Эту теорему мы даем здесь без доказательства.
Следствие 3.1. В силу Тезиса Тьюринга, любая интуитивно вычислимая функция может быть запрограммирована в терминах этих операций.
Следствие 3.2 Мы получили что-то вроде языка, на котором можно описывать новую Машину Тьюринга, используя описания уже существующих, а затем, используя теоремы 3.1 - 3.4, построить её функциональную схему.
Следствие 3.3 Алгоритм - это конструктивный объект. В случае Машины Тьюринга атомарными объектами являются команды, а теорема 3.5 определяет правила композиции.
Выводы:
Алгоритм - конструктивный объект;
Алгоритм можно строить из других алгоритмов;
o, ||, if_then_else, while_do - универсальный набор действий по управлению вычислительным процессом.
Вопросы :
Что такое правило подстановки?
Зависит ли результат от порядка следования правил в НАМ?
Что происходит когда не применимо ни одно правило подстановки?
Что утверждает тезис Маркова?
Можно ли доказать тезис Маркова?
Семантика операции o?
Семантика операции ||?
Семантика операции if_then_else?
Семантика операции while_do?
Что такое конструктивный объект?
Алгоритм - это конструктивный объект?
|
из
5.00
|
Обсуждение в статье: Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

