Постановка задачи и функция приспособленности

Пусть перед нами стоит задача оптимизации, например:

· Задача наилучшего приближения

o Если рассматривать систему n линейных уравнений с m неизвестными

Ax = b

в случае, когда она переопределена (n > m), то иногда оказывается естественной задача о нахождении вектора x, который "удовлетворяет этой системе наилучшим образом", т. е. из всех "не решений" является лучшим.

· Задача о рационе.

o Пусть имеется n различных пищевых продуктов, содержащих m различных питательных веществ. Обозначим через a_ij содержание (долю) j-го питательного вещества в i-ом продукте, через b_j — суточную потребность организма в j-ом питательном веществе, через c_i — стоимость единицы i-го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах

· Транспортная задача.

o Эта задача — классическая задача линейного программирования. К ней сводятся многие оптимизационные задачи. Формулируется она так. На m складах находится груз, который нужно развезти n потребителям. Пусть a_i (i = 1, ..., n) — количество груза на i-ом складе, а b_j (j = 1, ..., m) — потребность в грузе j-го потребителя, c_ij — стоимость перевозки единицы груза с i-го склада j-му потребителю. Требуется минимизировать стоимость перевозок.

· Задачи о распределении ресурсов.

o Общий смысл таких задач — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим простейший пример — задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p. Обозначим через x_j активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум m_j и максимум M_j вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны e_j(x). Требуется сгенерировать требуемую мощность p при минимальных затратах.[8]

Переформулируем задачу оптимизации как задачу нахождения максимума некоторой функции f(x₁, x₂, …, x_n), называемой функцией приспособленности (fitness function). Она должна принимать неотрицательные значения на ограниченной области определения (для того, чтобы мы могли для каждой особи считать её приспособленность, которая не может быть отрицательной), при этом совершенно не требуются непрерывность и дифференцируемость.

Каждый параметр функции приспособленности кодируется строкой битов.

Особью будет называться строка, являющаяся конкатенацией строк упорядоченного набора параметров (рис1):

 

1010 10110 101 … 10101

| x1 | x2 | x3 | … | xn |

Рис 1. Ионкатенационная строка упорядоченного набора параметров

 

Универсальность ГА заключается в том, что от конкретной задачи зависят только такие параметры, как функция приспособленности и кодирование решений. Остальные шаги для всех задач производятся одинаково.[9]

1.2 Принцип работы ГА

Генетические алгоритмы оперируют совокупностью особей (популяцией), которые представляют собой строки, кодирующие одно из решений задачи. Этим ГА отличается от большинства других алгоритмов оптимизации, которые оперируют лишь с одним решением, улучшая его.[10]

С помощью функции приспособленности среди всех особей популяции выделяют:

· наиболее приспособленные (более подходящие решения), которые получают возможность скрещиваться и давать потомство

· наихудшие (плохие решения), которые удаляются из популяции и не дают потомства

Таким образом, приспособленность нового поколения в среднем выше предыдущего.[11]

В классическом ГА:

· начальная популяция формируется случайным образом

· размер популяции (количество особей N) фиксируется и не изменяется в течение работы всего алгоритма

· каждая особь генерируется как случайная L-битная строка, где L — длина кодировки особи

· длина кодировки для всех особей одинакова[12]

Алгоритм работы

На рисунке 2  изображена схема работы любого генетического алгоритма:

Рис 2. Схема работы любого генетического алгоритма.

 

Шаг алгоритма состоит из трех стадий:

1. генерация промежуточной популяции (intermediate generation) путем отбора (selection) текущего поколения

2. скрещивание (recombination) особей промежуточной популяции путем кроссовера (crossover), что приводит к формированию нового поколения

3. мутация нового поколения [13]

 

Отбор

Промежуточная популяция — это набор особей, получивших право размножаться. Наиболее приспособленные особи могут быть записаны туда несколько раз, наименее приспособленные с большой вероятностью туда вообще не попадут.[14]

В классическом ГА вероятность каждой особи попасть в промежуточную популяцию пропорциональна ее приспособленности, т.е. работает пропорциональный отбор (proportional selection).

Существует несколько способов реализации данного отбора:

§ stochastic sampling. Пусть особи располагаются на колесе рулетки так, что размер сектора каждой особи пропорционален ее приспособленности. N раз запуская рулетку, выбираем требуемое количество особей для записи в промежуточную популяцию.

§ remainder stochastic sampling. Для каждой особи вычисляется отношение ее приспособленности к средней приспособленности популяции. Целая часть этого отношения указывает, сколько раз нужно записать особь в промежуточную популяцию, а дробная показывает её вероятность попасть туда ещё раз. Реализовать такой способ отбора удобно следующим образом: расположим особи на рулетке так же, как было описано. Теперь пусть у рулетки не одна стрелка, а N, причем они отсекают одинаковые сектора. Тогда один запуск рулетки выберет сразу все N особей, которые нужно записать в промежуточную популяцию.[15] Такой способ иллюстрируется рисунком 3:

Рис 3. Способ remainder stochastic sampling в реализации отбора

 

Скрещивание

Особи промежуточной популяции случайным образом разбиваются на пары, потом с некоторой вероятностью скрещиваются, в результате чего получаются два потомка, которые записываются в новое поколение, или не скрещиваются, тогда в новое поколение записывается сама пара.

      В классическом ГА применяется одноточечный оператор кроссовера (1-point crossover): для родительских строк случайным образом выбирается точка раздела, потомки получаются путём обмена отсечёнными частями [16] (рис.4).

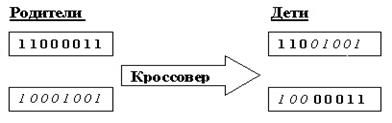Рис 4. Одноточечный оператор кроссовера

Мутация

К полученному в результате отбора и скрещивания новому поколению применяется оператор мутации, необходимый для "выбивания" популяции из локального экстремума и способствующий защите от преждевременной сходимости.

Каждый бит каждой особи популяции с некоторой вероятностью инвертируется. Эта вероятность обычно очень мала, менее 1% (рис 5).

1011001100101101 -> 1011001101101101Рис 5. Мутация

Можно выбирать некоторое количество точек в хромосоме для инверсии, причем их число также может быть случайным. Также можно инвертировать сразу некоторую группу подряд идущих точек.[17]

 

Критерии останова

Такой процесс эволюции, вообще говоря, может продолжаться до бесконечности, пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:

1. нахождение глобального, либо субоптимального решения;

2. исчерпание числа поколений, отпущенных на эволюцию;

3. исчерпание времени, отпущенного на эволюцию. Генетические алгоритмы служат, главным образом, для поиска решений в очень больших, сложных пространствах поиска.[18]