Методы продления службы рельсов . Черновой вариант

Аннотация.

Рассмотрены основные причины выхода из строя рельсов, введено понятие ЖКЕ, рассмотрены некоторые примеры перехода режимов течения, рассмотрена гидродинамическая модель взаимодействия колеса и рельса, рассмотрено уравнение Навье-Стокса, рассмотрена химическая модель системы с переменной вязкостью и его методы упрощения, рассмотрена возможная технология укрепления прочности рельсов. Здесь описывается идея упрочнения рельс с помощью возможности изменения вязкости материала, из которого он состоит, а также последующей диссипации энергии остаточных деформаций через решение уравнения Навье-Стокса в приближении Буссинеска — Обербека.  Введено понятие псевдокристаллической решетки, рассмотрена вязкость возле предела текучести, рассмотрены типы возможных соударений между частицами. Рассмотрена модель Эйнштейна для вязкости, рассмотрены основные реологические законы.

 Ключевые слова: рельс, вязкость, псевдокристаллическая решетка, колесо, уравнение Навье-Стокса

Железнодорожный транспорт является одной из самых металлоемких отраслей промышленности. Поэтому очень актуальными являются методы экономии металла. Около 39% всего металла расходуется на изготовление рельс, креплений для них, стрелочных переводов. Рассмотрим возможный метод экономии металла. Причиной выхода из строя рельс часто бывают дефекты, такие, как трещины, пустоты и пр., которые возникают при их изготовлении, а также трещины, изломы и пр., которые возникают в процессе эксплуатации. Здесь не рассматриваются причины выхода рельс из строя при их изгибе, смятии, износа верхнего слоя головки рельс. Основные причины износа рельс являются повышенные динамические нагрузки; удары по рельсам, падения некоторых грузов на рельсы. Здесь не рассматриваются причины износа рельс в результате коррозии, недостаточноv качествt содержания пути, нарушения технологии изготовления и пр. дефектов подобного характера.

Поместим, без объяснения на данном этапе, внутри рельса, по всей его длине, капсулу со смешанным оксидом железа, а также металлом, который не образует с ним амальгаму. На рисунке 1 капсула заштрихована красным цветом. Её точное расположение должно устанавливаться эмпирическим путем.

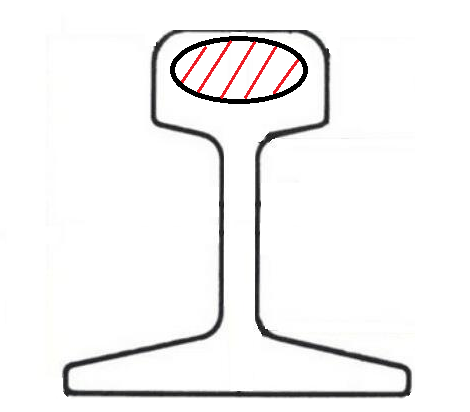
(рис. 1)

Введем понятие жидкой кинетической единицы (ЖКЕ), то есть некоторой объекта единичной массы в кг, который способен переносить единицу энергии в Дж при токе, или при разжижжении, или наоборот, затвердевании. Говорим о единице измерения ЖКЕ как кг*Дж.

Введем понятие псведокристаллической решетки. Известно, что существуют кристаллические и амфотерные тела. [5] Для введения понятия вязкости возле предела текучести рассмотрим жидкую кинетическую единицу. Рассмотрим каплю жидкости, тогда для применения идеи о жидкой частице (ЖКЕ) ограничим её объем до dV. Из первого начала термодинамики следует, что работа может тела совершаться только из запасенной энергии в виде некого потенциала, как переход в потенциальной яме из верхнего положения, удовлетворяющего критерию максимальной энергии в нижнее положение, удовлетворяющего критерию минимальной энергии.

Так как здесь говорится о работе жидкой частицы, потенциальную яму можно рассматривать как разность высот, во время перекачки по трубке тока насосом-двигателем, из нижней отметки с индексом высоты h₁=0, равной минимуму потенциальной энергии, в верхнюю отметку высоты с индексом h₂=H, равной максимуму потенциальной энергии. Часть работы потока по перемещению жидкой частицы можно рассмотреть, как dW=PdV.

Тогда работа давления насоса-двигателя, перекачивающего жидкость

.

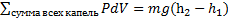Где m – масса жидкости, равная сумме средней массы одной капли.

Согласно фундаментальному определению первого начала термодинамики количество теплоты Q, переданное телу, идёт на изменение внутренней энергии тела U и на совершение телом работы A. Использование первого начала термодинамики в «обратную сторону» означает, что часть работы, совершаемой над телом рассеивается в виде тепла – диссипация энергии. Согласно представлениям молекулярно-кинетической теории (МКТ), количество теплоты есть мера средней кинетической энергии частиц (молекул, ионов, атомов и пр.). Соответственно, увеличение теплоты молекул увеличивает скорость либо колебаний около положения равновесия в твердом теле, либо среднюю скорость теплового движения в жидкостях и газах. Однако, в каждом из описанных случаев увеличение температуры ведет к увеличению частоты соударений между частицами твердого тела.

Согласно классической механики возможны три случая соударения для тел с микропараметрами: два предельных случая, а именно абсолютно упругий, где частица не теряет кинетической энергии, а только лишь изменяет свою траекторию, абсолютно неупругий, где частица полностью передает энергии телу, с которым столкнулось, и один промежуточный тип соударения, где частица передает лишь часть своей кинетической энергии.

Или с точки зрения формул: абсолютно упругий удар,

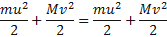
Абсолютно неупругий удар,

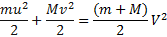
Промежуточный тип соударения,

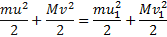
Где m – масса первой частицы, M – масса второй частицы, u – скорость первой частицы до соударения (в случае абсолютно упругого удара и после соударения), v – скорость второй частицы до соударения (в случае абсолютно упругого удара и после соударения), V – скорость конгломерата частиц после соударения, u₁ – скорость первой частицы после соударения, v₁ – скорость второй частицы после соударения.

Из-за того, что рассматриваемая модель используется для тел с микропараметрами, в расчетах с высокой точностью можно принять каждый исход столкновения дискретным с равновероятным итогом. Более того, из-за несимметричности частиц результатом столкновения возможен переход кинетической энергии поступательного движения в кинетическую энергию вращающегося тела.

В описанных формулах самыми интересными является вторая и третья. С точки зрения микромолекулярной структуры такие столкновения приводят к локальному запасу кинетической энергии. В МКТ известна прямая связь между скоростью диффузии и средней кинетической энергией частиц. На практике это означает, что в локальной зоне увеличенное число частиц способно преодолевать барьер, за которым начинается действие поверхностных сил. В конечном итоге это приводит к образованию временных конгломератов, которые носят названия псевдокристаллической решетки.

При образовании решетки подобного типа течение осуществляется как течение полностью неразрушенной структуры, вязкость которой η₂ значительно выше вязкости ЖКЕ η (η₂>> η), однако ниже вязкости кристаллической решетки η₁ (η₂< η₁). Объясню это на примере.

В стандартных условиях водяной пар представляет из себя комплекс из отдельных молекул воды с общей химической формулой n×H₂O, где n – число частиц испарившейся жидкости. [5] Во время охлаждения происходит охлаждение, некий вид полимеризации, молекулы при недостатке кинетической энергии попадают под действие поверхностных сил, образуя «упаковки» - структуры из набора небольшого числа молекул с общей формулой (H₂O)_k, где k – число среднее молекул одной упаковки. [6] Реакция конденсации выглядит примерно таким образом:

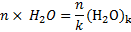
Упаковки характеризуются уже тем, что молекулы способны при столкновениях, теряя всю кинетическую энергию на время «застревать» около положений равновесия, это и понятно – диффузия подразумевает локальное поднятие или опускание температуры в некоторой области пространства объемом dV. При дальнейшем опускании температуры молекулы воды все сильнее подвержены полимеризации, т.е. увеличению размеров «упаковки» путем увеличения числа молекул в ней. Образование «упаковки» ведет к все большему увеличению числа молекул, которые пересекают действие поверхностных сил уже образовавшихся конгломератов. Это обозначает возникновение все большего числа молекул, которые на некоторое время занимают положение равновесия на короткие промежутки времени, что характеризует образование псевдокристаллической решетки и локальное увеличение вязкости. [5]

При дальнейшем охлаждении «упаковки» начинают полимеризоваться. Наглядно это выглядит как переход водной газовой взвеси в жидкость. Такую реакцию можно записать как:

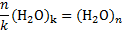
Такое явление сопровождается еще большим увеличением параметра вязкости благодаря увеличению поверхностной площади, по которой «упаковки» контактируют между собой в структуре полимера. Как понятно из примера, дальнейшее охлаждение приводит лишь к ещё большему увеличению конгломератов с псевдокристаллической решеткой. Более того, при выпадении в осадок в нестерильной среде жидкости адсорбирует на себя пыль из окружающего воздуха, которая принимает на себя роль центров кристаллизации. В конечном итоге около точки замерзания участков с псевдокристаллической решеткой накапливается такое число, что энергии диффузии не хватает для их разрушения, после чего структура начинает замерзать, образуя полноценную кристаллическую решетку с параметром вязкости, наиболее приближенному к максимальной вязкости.

Однако, по прошествии времени из-за внутреннего испарения в узлах идеальной кристаллической решетки остается все меньше частиц, то есть возникают участки с некомпенсированной силой межмолекулярного взаимодействия. [5] Процессы диффузии снова начинают увеличиваться, что в дальнейшем приводит к уменьшению вязкости. То есть чем дольше находится жидкость в состоянии замороженного тела, тем большее её внутренняя структура напоминает псевдокристаллическую решетку. Наглядным примером служат лавины, где нижние слои воды под возрастом и внешним давлением теряют свои вязкостные характеристики идеальной кристаллической решетки. [5,3]

Хорошо, а какие процессы идут в аморфных веществах, в которых не образуется кристаллической решетки. В процессе охлаждении в аморфных веществах псевдокристаллические решетки увеличивают свое количество до такой степени, что, как и у кристаллических веществ энергии диффузии уже не хватает для поддержания структуры в разжиженном состоянии, что выглядит как затвердевание тела. Вязкость стремится к вязкости твердого тела с кристаллической решеткой. Однако, в данной структуре есть вероятность образования конгломератов со сверхпрочной псевдокристаллической решеткой, которая уже не разрушается за очень длительное время. Чем старше структура, тем большее количество конгломератов образуют особо прочные псевдокристаллические решетки, то есть структура все более напоминает строение кристаллического тела. На практике это выглядит, например, как увеличение колкости стекла со временем его выдержки.

Так, при увеличении ЖКЕ у некоторого объема сплошной среды, за исключением газовой фазы, возможны следующие случаи, за исключением случая с постоянной вязкостью и отсутствием пределов текучести и затвердевания: стандартный случай, или режим течения Шведова-Бингама при увеличении нагрузки на сплошную среду. ЖКЕ увеличивается до определенного момента, после которого наступает предел текучести, и твердая фаза переходит в жидкую, то есть, разжижается. Затем, при дальнейшем увеличении ЖКЕ к данной среде применяются стандартные реологические модели. Это можно записать с помощью канонического уравнения [4]

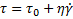
Режим течения Гершеля-Балкли. Рассмотрим раствор глины в воде, который представляет из себя тиксотропную жидкость. В условиях без нагрузки, он представляет из себя дисперсную среду с наличием довольно крупных конгломератов глины, которые при оказании минимальной динамической нагрузки, то есть увеличения ЖКЕ на некоторую бесконечно малую величину, способен слипаться в еще большие куски, сохраняя при этом свою общую вязкость путем увеличения локальной вязкости конгломератов и уменьшения локальной вязкости воды, так как из неё удаляется примесь глины. Однако, при увеличении динамической нагрузки, достигается предел прочности отдельных конгломератов после чего они начинают разрушаться и переходят в раствор. То есть, достигается общий предел текучести среды, после которого она переходит из твердой фазы в разжиженную. Скорость увеличения вязкости раствора значительно меньше скорости падения вязкости конгломератов, поэтому при увеличении ЖКЕ раствора, вязкость его начинает падать по степенному закону, или в виде канонического уравнения [4]

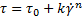
Режим течения Оствальда-де Виля. Рассмотрим эмульсию муки в воде, которая представляет из себя коллоидный раствор. Здесь без динамической нагрузки частицы муки свободно плавают в жидкости, так, что вязкость подчиняется закону Эйнштейна с инвариантами [3]

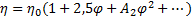
Однако, при увеличении ЖКЕ, жидкость между частицами твердой фазы выдавливается, подобно глиняным растворам, но здесь частицы гораздо более маленького размера, чем конгломераты глины, поэтому удельная прочность из значительно выше. В следствие этого, частицы не распадаются, а слипаются, образуя комплексы, подобные тромбам крови, у которых возникает колоссальная вязкость и возникает сначала псведокристаллическая решетка, а затем нарастающий до определенного момента, предел затвердевания (нижний предел текучести), с наступлением которого, система твердеет. Чтобы её обратно перевести в разжиженное состояние, то есть достижение верхнего предела текучести, требуется куда больше ЖКЕ, чем система обладает без нагрузки.

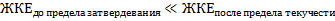
Стоит отметь, что у покоящейся жидкости ЖКЕ не равна нулю, доказательством этого является уравнение Навье-Стокса в приближении Буссинеска — Обербека [2], которое связывает гидродинамические и термодинамические параметры сплошной среды. Уравнение течения, которому подчиняется данная система сплошной среды, можно представить, как [4]

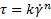
Таким образом, можно выделить следующие режимы течения: течение с пределом текучести и постоянной вязкостью, течение с пределом текучести и понижающейся вязкостью, течение с увеличивающейся вязкостью и возникновением нижнего предела текучести и с последующим разрушением верхнего предела текучести.

Перейдем непосредственно к методам увеличения службы рельс. Рассмотрим гидродинамическую модель взаимодействия колеса и рельса. Материал рельс можно представить, как очень вязкую жидкость. Согласно гидродинамической модели, при воздействии на жидкость динамической нагрузкой возникает ударная волна, впереди которой движется фронт сильного разрыва, который сопровождается скачком ряда термодинамических величин. Соответственно, при движении колеса по рельсу, верхняя площадка рельса определенной толщины ∆h деформируется (прогибается), образуя фронт сильного разрыва, который движется впереди рельса. Фронт сильного разрыва характеризуется скачком давления. Перейдем к записи давления в канонической формуле.

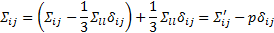
Где  – тензор полного напряжения,  - тензор без учета давления. Известно из опытов Паскаля, давление распространяется равномерно во все стороны, то есть, давление представляет из себя сферический тензор. Однако, при взаимодействии колеса и рельса возникает одноосное сжатие. Его можно рассмотреть, как одноосное растяжение с противоположным знаком. Сонаправим 1-ую компоненту первого скалярного инварианта (то есть, 1-ый член следа тензора второго ранга) с осью oX. Найдем направление оси oX. Рассмотрим удельное напряжение, возникающее при изгибе поверхности головки рельса колесом. Вычислим направление главного вектора силы удельного напряжения в направлении движения колеса по теореме параллелограмма (рис.2).

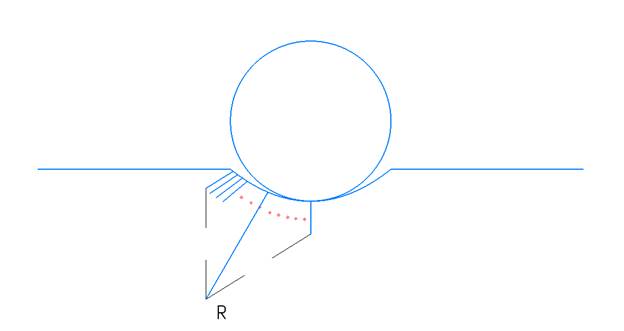
(рис.2)

Вычислим равнодействующую от главного вектора силы удельного напряжения и силы тяжести, оказываемой колесом на поверхность головки рельса (рис.3)

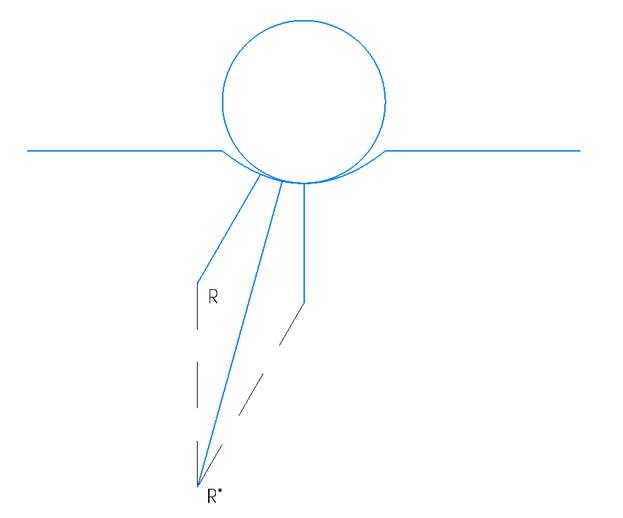
(рис.3)

Сонаправим ось oX с равнодействующей силы.

Тензор одноосного растяжения записывается как

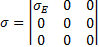
Разделим тензор одноосного сжатия на гидростатическую и девиаторную компоненты [1], или

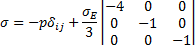
Из приведенной формулы видно, что реакция на 1-ую компоненту первого скалярного инварианта в 4 раза больше, чем на две другие. Перейдем к записи уравнения Навье-Стокса [2], или

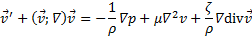
Где 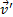 - обозначает частную производную скорости по времени,  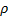– плотность,  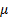– кинематическая вязкость,  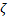– вторая вязкость.

Мы пренебрегаем вязкостью в слагаемом с дивергенцией скорости, а именно:

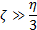
Перепишем данное уравнение по координатам, введя оператор дифференцирования, равный 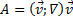, с соответствующим индексом по координате, а также учтя, что член локального ускорения (частная производная скорости по времени) обозначает удельную силу по соответствующей координате её единицу измерения, или имеем систему, заменим член при дивергенции скорости на вязкую компоненту силы, возникающую при проходе ударных волн:

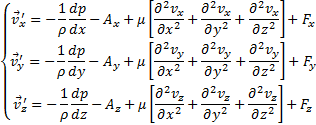
Применим к данной системе приближение Осеена, которое используется при течении при малых числах Рейнольдса. Имеем:

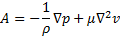
Данное приближение показывает, что при нахождении жидкости в капсуле без нагрузки, градиентом давления и членом с кинематической вязкостью можно пренебречь. Однако, при прохождении сквозь жидкость фронта сильного разрыва, возникает, как уже упоминалась, скачок давления. Рассмотрим локальное поле скоростей (частная производная скорости по времени). Оно является функцией поля одномерных градиентов давления. Значит, при сжатии/растяжении материала по какой-то координате возникает изменение скорости движения сплошной среды. Если мы рассматриваем кристаллическую решетку, то известно, что молекулы колеблются возле положений равновесия, однако сами положения равновесия способны двигаться.[5] Таким образом, кристаллическая решетка рассматривается как очень вязкая жидкость.

Известно, уравнения вязкости невозможно представить в тензорном виде, также, как и нет общего решения уравнения Навье-Стокса, но данное уравнение вполне решается по координатным осям. Градиент напряжения по оси oX в четыре раза больше, чем по двум другим осям.

Упростим уравнение Навье-Стокса. Рассмотрим оператор Лапласа

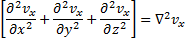
Так как ударная волна сонаправлена с осью oX, то возникающие продольные волны практически не распространяются по оси oZ, проекция которой на горизонтальную ось совпадает с проекцией на эту же ось координатной оси Ox, и полностью отсутствует по поперечной оси oY (рис.4)

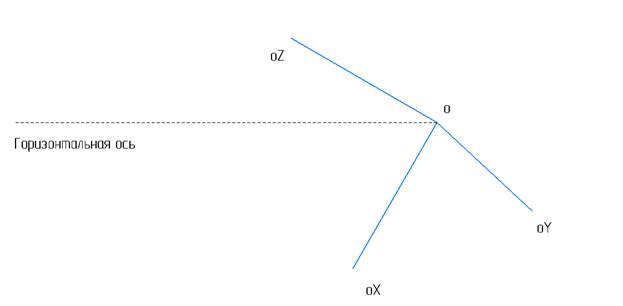
(рис.4)

Таким образом, после прохождения фронта сильного разрыва, одномерный оператор Лапласа по координате oY от скорости равен нулю, одномерный оператор Лапласа по координате oZ быстро убывает с увеличением расстояния и в пределе на бесконечности равен нулю, после чего достаточно рассмотреть только одномерный оператор Лапласа по координате oX, который сохраняется на бесконечности в виде следа, или

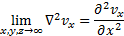
Тоже самое допущение применяется и к оператору A_x. Рассмотрим компоненту F_x, которая после аналогичных упрощений принимает вид

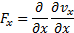
Перепишем уравнение Навье-Стокса с данным учетом, а также допустим, что сплошная среда рельс практически несжимаемая, или

 

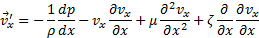
Таким образом, мы переходим к уравнению, в котором кинематическая вязкость находится только в одном члене.

Поместим в капсулу некоторую эмульсию, с компонентами, один из которых неорганическое соединение с сильным смещением электронной плотности, или вообще, с некомпенсированной электронной плотностью, а другой компонент - металл с низкой электроотрицательностью. Рассмотрим образование псевдокристаллической решетки в эмульсии крахмал плюс вода. Так как в молекуле крахмала есть свободные валентные связи, соответственно, возникает некомпенсированная электронная плотность, однако, в воде молекулы крахмала не растворяются, то есть реакция вида

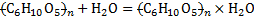
не идет, а значит, при удалении воды, молекулы крахмала полимеризуются, образуя укрупняющиеся конгломераты.

Если мы берем смешанный оксид железа, то смещение электронной плотности происходит к положениям 1,2 (рис.5).

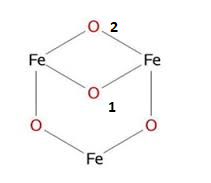
(рис.5)

Таким образом, при достаточном сближении молекул смешанного оксида железа, атом железа, находящийся на рисунке в нижнем положении присоединяется к атому кислорода в положении 2, возникает псевдокристаллическая решетка, при том, чем сильнее молекулы прижимаются друг к другу, тем более высокая прочность этой решетки. Если мы берем металл с достаточно низкой вязкостью, который не образует амальгаму с железом, то есть реакция вида

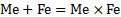
не идет, где Ме – некоторый металл, то при динамической нагрузке происходит образование псевдокристаллической решетки по модели, описанной выше.

Здесь также возможно использовать оксид алюминия или оксид железа-3, у которых электронная плотность смещается к положениям 1-го и последнего атомов кислорода.

Здесь, при создании определенного процентного содержания компонентов, возможно, эмпирическим путем закрепления параметров, решить систему вида

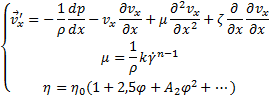
Результатом решения данной системы можно создать эмульсию, которой заполняется капсула рельса. При динамической нагрузке она упрочняется, поглощая в себя разрушающие вибрационные нагрузки, а затем, согласно приближению Буссинеска — Обербека, диссипируется в виде тепловой энергии, тем самым увеличивая срок службы рельс. Таким образом, устраняется проблема наличия дефектов рельс после их изготовления, а также практически полностью исключается возможность их появления в процессе эксплуатации.

Список литературы:

1. Основы реологии. А.Я. Малкин. Издательство профессия. Санкт-Петербург, 2018 г.

2. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. VI. Гидродинамика. — 5-е изд., стереот.-М .: ФИЗМАТЛИТ, 2001.-736 с.-ISB N 5-9221-0121-8 (Т. VI)

3. Реология дисперсных систем. Министерство высшего и среднего образования РСФСР. Е.Е. Бибик. Издательство Ленинградского университета. Ленинград, 1981 г.

4. Малкин А.Я., Исаев А.И. Реология: концепции, методы, приложения/ Пер. с англ. – СПб.: Профессия, 2007. – 560 стр., ил.

5. Собрание избранных трудов. Кинетическая теория жидкости. Академия наук СССР. Я.И. Френкель. Издательство академии наук СССР. Москва, Ленинград, 1959 г.