 |
Главная |
Математическое описание плоских геометрических проекций
|
из
5.00
|
Каждую из проекций можно описать матрицей 4´4. Этот способ оказывается удобным, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования.
Центральная (перспективная)проекция получается путем перспективного преобразования и проецирования на некоторую двухмерную плоскость «наблюдения». Перспективная проекция на плоскость Z = 0 обеспечивается преобразованием
[X Y Z H] = [x y z 1]*  = [x y 0 (rz+1)].
= [x y 0 (rz+1)].

Рис. 6.15. Вычисление одноточечной перспективы
или x* =  =
=  ;
;
y* =  =
=  ;
;
z* =  =
=  ,
,
где r =  .
.
Центр проекции находится в точке с координатами (0,0,-k) (рис. 6.15), плоскость проецирования Z = 0. Соотношения между x, y и x*, y* остаются теми же самыми. Рассматривая подобные треугольники, получим, что
 =
=  , или x* =
, или x* =  ;
;
аналогично y* =  .
.
Координаты x*, y* являются преобразованными координатами. В перспективном проектировании преобразованное пространство не является евклидовым, так как ортогональность осей не сохраняется. При k = ¥ получим аксонометрическое преобразование.
Аффинное преобразование есть комбинация линейных преобразований, сопровождаемых переносом.
Последний столбец в обобщенной матрице 4´4 должен быть равен:
 ,
,
в этом случае H = 1.
Перспективному преобразованию может предшествовать произвольная последовательность аффинных преобразований. Таким образом, чтобы получить перспективные изображения из произвольной точки наблюдения вначале используют аффинные преобразования, позволяющие сформировать систему координат с осью Z вдоль желаемой линии визирования. Затем применяется перспективное преобразование.
Аналогично перспективное преобразование, когда картинная плоскость перпендикулярна оси Z и совпадает с плоскостью Z = 1/r. Центр проекции находится в центре координат:
[X Y Z H] = [x y z 1] *  = [x y z (rz+1)] — одноточечная перспектива (точка схода Z);
= [x y z (rz+1)] — одноточечная перспектива (точка схода Z);
 — точка схода X.
— точка схода X.
Двухточечная (угловая) перспектива.Для получения двухточечной перспективы в общей матрице преобразования устанавливают коэффициенты p и q:
(x', y', z', 1) = (x, y, z, 1) 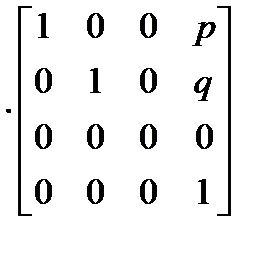 =[x, y, 0, (px+qu+1)];
=[x, y, 0, (px+qu+1)];
(x', y', z', 1) =  .
.
Такое преобразование приводит к двум точкам схода. Одна расположена на оси X в точке (  , 0, 0, 1), другая на оси Y в точке (0,
, 0, 0, 1), другая на оси Y в точке (0,  , 0, 1).
, 0, 1).
Рассмотрим это преобразование на получение проекции единичного куба (рис. 6.16).
| A |
| D |
| I |
| G |
| E |
| F |
| B |
| C |
| x |
| А |
| B |
| F |
| E |
| C |
| G |
| I |
| D |
| y |
| x |
| z |
Рис. 6.16. Единичный куб для получения двухточечной проекции
 .
.
В результате получаем проекцию вида, представленного на рис. 6.17.
| E',F' |
| A',B' |
| 0,91 |
| 0,83 |
| G',I' |
| C',D' |
| x |
| y |
| К точке схода на оси X |
| К точке схода на оси Y |
Рис. 6.17. Двухточечная проекция единичного куба
 =[x y z (px+qy+rz+1)] — трехточечная (косая) перспектива.
=[x y z (px+qy+rz+1)] — трехточечная (косая) перспектива.
Для того чтобы создать диметрическую проекцию, необходимо выполнить следующее условие:
sin2φ=sin2θ/(1- sin2θ).
Одним способом выбора sinθ является сокращение оси Z в фиксированное число раз. При этом единичный вектор на оси Z, равный [0 0 1 1], преобразовывается к виду
[X Y Z H] = [sinφ -cosφ×sinθ cosφ×cosθ 1]
или x* = sinφ;
y*= - cosφ sinθ.
Таким образом, для диметрической проекции получаем
φ = 20,705°:
θ = 22,208°.
Для образования изометрической проекции нужно в одинаковое число раз сократить все три оси. Для этого необходимо, чтобы выполнялось условие
sin2φ=sin2θ/(1- sin2θ) и sin2φ=(1-2sin2θ)/(1- sin2θ).
Таким образом,
φ = 35,26439°;
θ = 45°.
Рассмотрим теперь косоугольную проекцию(рис. 6.18), матрица может быть записана исходя из значений a и l.
Проекцией точки P(0,0,1) является точка P¢(l cosa, l sina, 0), принадлежащая плоскости xy. Направление проецирования совпадает с отрезком РР¢, проходящим через две эти точки. Это направление есть Р¢-Р = (l cosa, l sina, -1). Направление проецирования составляет угол b с плоскостью xy.
Теперь рассмотрим проекцию точки x, y, z и определим ее косоугольную проекцию (xp yp) на плоскости xy:
xp = x + z(l cosa);
yp = y + z(l sina).
Таким образом, матрица 4´4, которая выполняет эти действия и, следовательно, описывает косоугольную проекцию, имеет вид
Мкос=  .
.
 Рис. 6.18. Вычисление косоугольных проекций
Рис. 6.18. Вычисление косоугольных проекций
Применение матрицы Мкос приводит к сдвигу и последующему проецированию объекта: плоскости с постоянной координатой z = z1 переносятся в направлении x на z1 l cosa и в направлении y на z1 l sina и затем проецируется на плоскость z = 0. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных оси z.
Для проекции Кавалье l = 1, поэтому угол b= 45°. Для проекции Кабине l=½, а b = arctg(2) = 63,4°. В случае ортографической проекции l = 0 и b = 90°, поэтому матрица ортографического проецирования является частным случаем косоугольной проекции.
|
из
5.00
|
Обсуждение в статье: Математическое описание плоских геометрических проекций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

