 |
Главная |
Обработка результатов неравноточных измерений
|
из
5.00
|
При обработки неравноточных измерений вводят новую характеристику точности измерения, называемую весом измерения. Вес измерения определяется формулой 3.1.
 , (3.1)
, (3.1)
где k – произвольно выбранное число, но одно и то же для всех весов, участвующих в решении какой-либо задачи. Вследствие того, что точное значение дисперсии 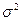 никогда неизвестно, вес находят по формуле 3.2.
никогда неизвестно, вес находят по формуле 3.2.
 , (3.2)
, (3.2)
где средняя квадратическая погрешность т определена по достаточно большому количеству результатов измерений.
Пример 1: Найти вес превышения, полученного в результате геометрического нивелирования хода длиной L. Известно, что  . Подставим это выражение для
. Подставим это выражение для  в формулу (3.2)
в формулу (3.2)  получим
получим  . Обозначим
. Обозначим 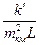 буквой k и будем иметь:
буквой k и будем иметь: 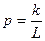 .
.
Таким образом, вес превышения по всему ходу геометрического нивелирования обратно пропорционален длине хода..
Если известны веса аргументов функции, то можно найти и вес самой функции. Для различных видов функций можно вывести формулы, по которым определяются веса этих функций. При k=1 вес р равен  , откуда
, откуда 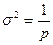 . Величину
. Величину  называют обратным весом.
называют обратным весом.
1. Функция общего вида 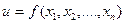

2. Линейные функции 

так как 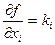 =>
=> 
3. 
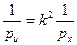
4.  ;
;  здесь
здесь  поэтому
поэтому 
В случае равноточных измерений, при  будет
будет  откуда
откуда  .
.
Пример 1: Найти вес произведения 2β, если вес угла β = 1.
По формуле 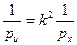 имеем
имеем  откуда
откуда  .
.
При оценке точности неравноточных измерений в качестве единицы меры дисперсией принимают дисперсию  измерения, вес которого равен единицы. Так как значение стандарта
измерения, вес которого равен единицы. Так как значение стандарта  неизвестно, то практически его заменяют средней квадратической погрешностью μ , соответствующей измерению с весами, равным единицы, и ряда краткости называют средней квадратической погрешностью единицы веса, которая определяется по формулам 3.3 и 3.4.
неизвестно, то практически его заменяют средней квадратической погрешностью μ , соответствующей измерению с весами, равным единицы, и ряда краткости называют средней квадратической погрешностью единицы веса, которая определяется по формулам 3.3 и 3.4.
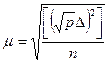 (3.3) или
(3.3) или  (3.4)
(3.4)
Арифметическая средина может быть записана в виде 3.5
 (3.5) ,
(3.5) ,
а с приближенными значениями эта формула имеет вид 3.6
 (3.6), где
(3.6), где 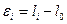
Поправка: 
Средняя квадратическая погрешность единицы веса через вероятнейшие поправки выражается по формуле 3.7
 (3.7)
(3.7)
Средняя квадратическая погрешность общей арифметической средины имеет вид 3.8
 (3.8) или
(3.8) или  (3.9)
(3.9)
выражение 3.9 - выражение средней квадратической погрешности общей арифметической средины через вероятнейшие поправки
Контрольные вычисления 
1) 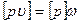
2) 
Определение средней квадратической погрешности единицы веса, если в разностях нет систематической погрешности, определяется по формуле 3.10.
 (3.10)
(3.10)
В случае наличия систематических погрешностей последние предварительно исключают из разностей. Систематическая погрешность обозначается Θ (i=1,2,…,п). Величина Θ называется коэффициентом систематического влияния в разностях
двойных измерений или коэффициентом остаточного систематического влияния и определяется по формуле 3.11.
 (3.11)
(3.11)
При расчете двойных линейных измерений, если в разностях нет систематических погрешностей, средняя квадратическая погрешность единицы веса может быть определена по формуле 3.12.
 (3.12)
(3.12)
Если в разностях имеется систематическая погрешность, то средняя квадратическая погрешность единицы веса вычисляется по формуле 3.13.
 (3.13)
(3.13)
Приложение А
ЗАДАЧА 1
1-5.Стороны прямоугольника а и b измерены с точностью ma и mb. Найти среднюю квадратическую погрешность площади прямоугольника.
| Параметры | Варианты 1 - 5 | ||||
| ma | 0,01 | 0,02 | 0,02 | 0,05 | 0,02 |
| mb | 0,02 | 0,01 | 0,05 | 0,02 | 0,03 |
| а | 270,21 | 242,24 | 242,24 | 262,35 | 362,62 |
| b | 360,52 | 371,01 | 275,05 | 252,24 | 362,62 |
6-10.Стороны треугольника a, b, c измерялись с точностью ma, mb, mc. Найти среднюю квадратическую погрешность измерения площади треугольника.
| Параметры | Варианты 6 - 10 | ||||
| ma | 0,02 | 0,02 | 0,01 | 0,05 | 0,05 |
| mb | 0,02 | 0,01 | 0,02 | 0,02 | 0,05 |
| mc | 0,01 | 0,01 | 0,02 | 0,02 | 0,02 |
| a | 200,24 | 300,36 | 272,61 | 255,55 | 155,95 |
| b | 200,24 | 220,21 | 324,76 | 272,72 | 255,95 |
| c | 300,36 | 272,61 | 198,52 | 262,62 | 165,65 |
11-15.Определить среднюю квадратическую погрешность угла, измеренного двумя приемами, если средняя квадратическая погрешность одного полуприема mβ.
| Параметры | Варианты 11 - 15 | ||||
| mβ | 5˝ | 15˝ | 2˝ | 1˝ | 30˝ |
16-20.Найти среднюю квадратическую погрешность суммы углов n-угольника, если углы измерялись с точностью.
| Параметры | Варианты 16 - 20 | ||||
| mβ | 5˝ | 2˝ | 1˝ | 15˝ | 30˝ |
| n |
21-25.Стороны прямоугольника a и b измерялись со средними квадратическими погрешностями ma и mb. Найти среднюю квадратическую погрешность измерения периметра прямоугольника
| Параметры | Варианты 21 - 25 | ||||
| ma | 0,02 | 0,01 | 0,02 | 0,05 | 0,01 |
| mb | 0,01 | 0,02 | 0,05 | 0,02 | 0,05 |
| a | 342,64 | 532,91 | 721,22 | 645,45 | 378,59 |
| b | 621,71 | 624,24 | 236,5 | 232,68 | 365,95 |
| Параметры | Варианты 26 - 30 | ||||
| ma | 0,01 | 0,02 | 0,05 | 0,02 | 0,05 |
| mb | 0,02 | 0,01 | 0,02 | 0,05 | 0,01 |
| a | 234,64 | 253,91 | 271,22 | 465,45 | 837,59 |
| b | 216,71 | 264,24 | 623,5 | 322,68 | 635,95 |
26-30.Найти среднюю квадратическую погрешность вычисления площади круга, если диаметр круга d определялся с точностью md.
| Параметры | Варианты 31 - 35 | ||||
| md | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 |
| d | 241,53 | 362,42 | 271,45 | 362,62 | 251,49 |
| Параметры | Варианты 36 - 40 | ||||
| md | 0,01 | 0,07 | 0,08 | 0,09 | 0,01 |
| d | 541, 23 | 632, 24 | 217, 54 | 236, 26 | 521,47 |
Задача 2
Произвести обработку ряда равноточных измерений угла: 1)найти среднее арифметическое значение, 2)среднюю квадратическую погрешность одного измерения, 3) среднюю квадратическую погрешность арифметическойсредины (вероятнейшего значения)
| № изм | Варианты | ||||||
| 143˚43΄43˝ | 158˚24΄51˝ | 191˚32΄32˝ | 151˚24΄29˝ | 147˚18΄18˝ | 173˚18΄19˝ | 101˚10΄52˝ | |
| 143˚43΄47˝ | 158˚24΄54˝ | 191˚32΄38˝ | 151˚24΄24˝ | 147˚18΄16˝ | 173˚18΄18˝ | 101˚10΄51˝ | |
| 143˚43΄47˝ | 158˚24΄47˝ | 191˚32΄35˝ | 151˚24΄25˝ | 147˚18΄22˝ | 173˚18΄20˝ | 101˚10΄53˝ | |
| 143˚43΄45˝ | 158˚24΄46˝ | 191˚32΄36˝ | 151˚24΄27˝ | 147˚18΄25˝ | 173˚18΄21˝ | 101˚10΄50˝ | |
| 143˚43΄47˝ | 158˚24΄52˝ | 191˚32΄34˝ | 151˚24΄22˝ | 147˚18΄17˝ | 173˚18΄17˝ | 101˚10΄52˝ | |
| 143˚43΄40˝ | 158˚24΄38˝ | 191˚32΄31˝ | 151˚24΄27˝ | 147˚18΄21˝ | 173˚18΄18˝ | 101˚10΄54˝ | |
| 143˚43΄44˝ | 158˚24΄52˝ | 191˚32΄37˝ | 151˚24΄22˝ | 147˚18΄20˝ | 173˚18΄21˝ | 101˚10΄55˝ | |
| № изм | Варианты | ||||||
| 202˚54΄31˝ | 247˚51΄29˝ | 143˚24΄01˝ | 123˚23΄13˝ | 122˚22΄22˝ | 164˚51΄08˝ | 172˚24΄24˝ | |
| 202˚54΄51˝ | 247˚51΄28˝ | 143˚24΄02˝ | 123˚23΄14˝ | 122˚22΄20˝ | 164˚51΄12˝ | 172˚24΄29˝ | |
| 202˚54΄53˝ | 247˚51΄30˝ | 143˚24΄03˝ | 123˚23΄15˝ | 122˚22΄18˝ | 164˚51΄13˝ | 172˚24΄23˝ | |
| 202˚54΄50˝ | 247˚51΄31˝ | 143˚24΄05˝ | 123˚23΄12˝ | 122˚22΄23˝ | 164˚51΄16˝ | 172˚24΄21˝ | |
| 202˚54΄52˝ | 247˚51΄27˝ | 143˚24΄04˝ | 123˚23΄10˝ | 122˚22΄21˝ | 164˚51΄10˝ | 172˚24΄25˝ | |
| 202˚54΄54˝ | 247˚51΄32˝ | 143˚24΄01˝ | 123˚23΄12˝ | 122˚22΄20˝ | 164˚51΄08˝ | 172˚24΄24˝ | |
| 202˚54΄55˝ | 247˚51΄30˝ | 143˚24΄02˝ | 123˚23΄13˝ | 122˚22΄23˝ | 164˚51΄12˝ | 172˚24΄24˝ | |
| № изм | Варианты | ||||||
| 162˚31΄33˝ | 126˚51΄29˝ | 264˚24΄24˝ | 173˚43΄19˝ | 96˚32΄54˝ | 280˚22΄01˝ | 359˚01΄24˝ | |
| 162˚31΄35˝ | 126˚51΄27˝ | 264˚24΄29˝ | 173˚43΄23˝ | 96˚32΄53˝ | 280˚22΄02˝ | 359˚01΄23˝ | |
| 162˚31΄37˝ | 126˚51΄35˝ | 264˚24΄25˝ | 173˚43΄41˝ | 96˚32΄52˝ | 280˚22΄03˝ | 359˚01΄25˝ | |
| 162˚31΄37˝ | 126˚51΄33˝ | 264˚24΄28˝ | 173˚43΄25˝ | 96˚32΄51˝ | 280˚22΄00˝ | 359˚01΄24˝ | |
| 162˚31΄39˝ | 126˚51΄31˝ | 264˚24΄27˝ | 173˚43΄32˝ | 96˚32΄50˝ | 280˚22΄04˝ | 359˚01΄26˝ | |
| 162˚31΄33˝ | 126˚51΄33˝ | 264˚24΄24˝ | 173˚43΄23˝ | 96˚32΄53˝ | 280˚22΄05˝ | 359˚01΄22˝ | |
| 162˚31΄31˝ | 126˚51΄35˝ | 264˚24΄25˝ | 173˚43΄33˝ | 96˚32΄56˝ | 280˚22΄02˝ | 359˚01΄28˝ | |
| № изм | Варианты | ||||||
| 300˚15΄05˝ | 280˚20΄10˝ | 160˚05΄20˝ | 52˚37΄41˝ | 41˚21΄54˝ | 89˚32΄59˝ | 273˚53΄03˝ | |
| 300˚15΄06˝ | 280˚20΄11˝ | 160˚05΄21˝ | 52˚37΄39˝ | 41˚21΄53˝ | 89˚32΄58˝ | 273˚53΄08˝ | |
| 300˚15΄04˝ | 280˚20΄12˝ | 160˚05΄23˝ | 52˚37΄40˝ | 41˚21΄52˝ | 89˚32΄53˝ | 273˚53΄07˝ | |
| 300˚15΄08˝ | 280˚20΄09˝ | 160˚05΄20˝ | 52˚37΄38˝ | 41˚21΄51˝ | 89˚32΄55˝ | 273˚53΄11˝ | |
| 300˚15΄09˝ | 280˚20΄08˝ | 160˚05΄19˝ | 52˚37΄36˝ | 41˚21΄48˝ | 89˚32΄52˝ | 273˚53΄12˝ | |
| 300˚15΄04˝ | 280˚20΄05˝ | 160˚05΄17˝ | 52˚37΄34˝ | 41˚21΄45˝ | 89˚32΄59˝ | 273˚53΄09˝ | |
| 300˚15΄02˝ | 280˚20΄02˝ | 160˚05΄15˝ | 52˚37΄32˝ | 41˚21΄42˝ | 89˚32΄58˝ | 273˚53΄10˝ | |
| № изм | Варианты | ||||||
| 234˚56΄55˝ | 281˚45΄34˝ | 95˚00΄34˝ | 109˚56΄34˝ | 342˚50΄37˝ | 36˚55΄05˝ | 252˚37΄41˝ | |
| 234˚56΄54˝ | 281˚45΄34˝ | 95˚00΄39˝ | 109˚56΄39˝ | 342˚50΄36˝ | 36˚55΄06˝ | 252˚37΄39˝ | |
| 234˚56΄49˝ | 281˚45΄34˝ | 95˚00΄40˝ | 109˚56΄40˝ | 342˚50΄35˝ | 36˚55΄04˝ | 252˚37΄40˝ | |
| 234˚56΄52˝ | 281˚45΄32˝ | 95˚00΄45˝ | 109˚56΄45˝ | 342˚50΄34˝ | 36˚55΄08˝ | 252˚37΄39˝ | |
| 234˚56΄51˝ | 281˚45΄31˝ | 95˚00΄44˝ | 109˚56΄44˝ | 342˚50΄33˝ | 36˚55΄09˝ | 252˚37΄36˝ | |
| 234˚56΄50˝ | 281˚45΄33˝ | 95˚00΄43˝ | 109˚56΄43˝ | 342˚50΄32˝ | 36˚55΄04˝ | 252˚37΄34˝ | |
| 234˚56΄48˝ | 281˚45΄30˝ | 95˚00΄37˝ | 109˚56΄37˝ | 342˚50΄33˝ | 36˚55΄02˝ | 252˚37΄31˝ | |
| № изм | Варианты | ||||||
| 324˚50΄55˝ | 233˚54΄31˝ | 295˚01΄34˝ | 189˚56΄34˝ | 242˚50΄37˝ | 136˚52΄05˝ | 52˚27΄41˝ | |
| 324˚50΄54˝ | 233˚54΄33˝ | 295˚01΄39˝ | 189˚56΄39˝ | 242˚50΄36˝ | 136˚52΄06˝ | 52˚27΄39˝ | |
| 324˚50΄49˝ | 233˚54΄34˝ | 295˚01΄40˝ | 189˚56΄40˝ | 242˚50΄35˝ | 136˚52΄04˝ | 52˚27΄40˝ | |
| 324˚50΄52˝ | 233˚54΄32˝ | 295˚01΄45˝ | 189˚56΄45˝ | 242˚50΄34˝ | 136˚52΄08˝ | 52˚27΄39˝ | |
| 324˚50΄51˝ | 233˚54΄34˝ | 295˚01΄44˝ | 189˚56΄44˝ | 242˚50΄33˝ | 136˚52΄09˝ | 52˚27΄36˝ | |
| 324˚50΄50˝ | 233˚54΄34˝ | 295˚01΄43˝ | 189˚56΄43˝ | 242˚50΄32˝ | 136˚52΄04˝ | 52˚27΄34˝ | |
| 324˚50΄48˝ | 233˚54΄30˝ | 295˚01΄37˝ | 189˚56΄37˝ | 242˚50΄33˝ | 136˚52΄02˝ | 52˚27΄31˝ |
Задача 3
Найти среднюю квадратическую погрешность одного измерения угла по
разностям двойных равноточных измерений.
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 163˚15΄24˝ | 163˚15΄31˝ | 143˚18΄21˝ | 143˚18΄28˝ | 153˚14΄31˝ | 153˚14΄39˝ | |
| 231˚24΄42˝ | 231˚24΄38˝ | 162˚58΄12˝ | 162˚58΄08˝ | 74˚21΄48˝ | 74˚21΄42˝ | |
| 78˚52΄04˝ | 78˚52΄09˝ | 69˚12΄51˝ | 69˚12΄47˝ | 265˚08΄52˝ | 265˚08΄56˝ | |
| 101˚49΄35˝ | 101˚49΄30˝ | 101˚49΄35˝ | 101˚49΄40˝ | 101˚49΄35˝ | 101˚49΄37˝ | |
| 84˚01΄39˝ | 84˚01΄43˝ | 207˚35΄44˝ | 207˚35΄49˝ | 208˚12΄12˝ | 208˚12΄07˝ | |
| 181˚29΄51˝ | 181˚29΄50˝ | 215˚53΄29˝ | 215˚53΄36˝ | 89˚52΄52˝ | 89˚52΄54˝ | |
| 232˚12΄48˝ | 232˚12΄41˝ | 71˚23΄13˝ | 71˚23΄07˝ | 123˚48΄48˝ | 123˚48΄57˝ | |
| № изм | ||||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 241˚41΄41˝ | 241˚41΄37˝ | 77˚29΄39˝ | 77˚29΄31˝ | 90˚58΄03˝ | 90˚58΄57˝ | |
| 68˚29΄35˝ | 68˚29΄37˝ | 161˚59΄59˝ | 162˚00΄06˝ | 239˚29΄29˝ | 239˚29΄31˝ | |
| 127˚31΄47˝ | 127˚31΄56˝ | 213˚13΄13˝ | 213˚13΄06˝ | 156˚34΄34˝ | 156˚34΄31˝ | |
| 79˚06΄08˝ | 79˚06΄12˝ | 148˚21΄38˝ | 148˚21΄32˝ | 198˚23΄18˝ | 198˚23΄12˝ | |
| 148˚05΄53˝ | 148˚05΄46˝ | 43˚38΄02˝ | 43˚38΄10˝ | 142˚15΄28˝ | 142˚15΄20˝ | |
| 99˚59΄24˝ | 99˚59΄21˝ | 271˚44΄25˝ | 271˚44΄21˝ | 168˚08΄08˝ | 168˚08΄09˝ | |
| 135˚28΄02˝ | 135˚28΄59˝ | 178˚12΄59˝ | 178˚12΄50˝ | 71˚48΄57˝ | 71˚48΄52˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 93˚08΄08˝ | 93˚08΄01˝ | 261˚51΄58˝ | 261˚51΄54˝ | 162˚24΄25˝ | 162˚24΄29˝ | |
| 125˚21΄59˝ | 125˚21΄56˝ | 143˚24΄26˝ | 143˚24΄28˝ | 176˚13΄13˝ | 176˚13΄12˝ | |
| 198˚29΄34˝ | 198˚29΄40˝ | 71˚32΄59˝ | 71˚32΄02˝ | 79˚59΄58˝ | 79˚59΄50˝ | |
| 235˚11΄21˝ | 235˚11΄23˝ | 238˚18΄04˝ | 238˚18΄00˝ | 161˚36΄42˝ | 161˚36΄38˝ | |
| 79˚59΄59˝ | 79˚59΄02˝ | 196˚51΄49˝ | 196˚51΄42˝ | 203˚48΄03˝ | 203˚48΄07˝ | |
| 135˚35΄41˝ | 135˚35΄36˝ | 178˚34΄29˝ | 178˚34΄21˝ | 154˚46΄28˝ | 154˚46΄20˝ | |
| 154˚47΄39˝ | 154˚47΄36˝ | 217˚17΄17˝ | 217˚17΄12˝ | 265˚15΄15˝ | 265˚15΄20˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 154˚54΄54˝ | 154˚54΄50˝ | 211˚11΄11˝ | 211˚11΄09˝ | 212˚12΄12˝ | 212˚12΄06˝ | |
| 79˚09΄27˝ | 79˚09΄22˝ | 193˚24΄24˝ | 193˚24΄29˝ | 139˚51΄24˝ | 139˚51΄28˝ | |
| 161˚12΄35˝ | 161˚12΄00˝ | 77˚53΄08˝ | 77˚53΄02˝ | 87˚37΄59˝ | 87˚37΄52˝ | |
| 183˚37΄29˝ | 183˚37΄25˝ | 161˚48΄37˝ | 161˚48΄31˝ | 161˚24΄02˝ | 161˚24΄59˝ | |
| 98˚36΄05˝ | 98˚36΄02˝ | 159˚07΄27˝ | 159˚07΄25˝ | 203˚03΄34˝ | 203˚03΄36˝ | |
| 213˚23΄48˝ | 213˚23΄53˝ | 232˚34΄58˝ | 232˚34΄55˝ | 181˚17΄16˝ | 181˚17΄13˝ | |
| 254˚18΄02˝ | 254˚18΄56˝ | 181˚54΄59˝ | 181˚54΄56˝ | 152˚36΄37˝ | 152˚36΄00˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 213˚13΄13˝ | 213˚13΄08˝ | 114˚54΄14˝ | 114˚54΄12˝ | 215˚15΄15˝ | 215˚15΄10˝ | |
| 151˚24΄27˝ | 151˚24΄22˝ | 96˚21΄37˝ | 96˚21΄31˝ | 115˚15΄15˝ | 115˚15΄09˝ | |
| 78˚27΄59˝ | 78˚27΄03˝ | 121˚39΄41˝ | 121˚39΄45˝ | 74˚23΄58˝ | 74˚23΄02˝ | |
| 161˚43΄36˝ | 161˚43΄31˝ | 78˚59΄31˝ | 78˚59΄26˝ | 98˚33΄41˝ | 98˚33΄46˝ | |
| 99˚21΄48˝ | 99˚21΄42˝ | 153˚01΄01˝ | 153˚01΄54˝ | 167˚47΄03˝ | 167˚47΄59˝ | |
| 139˚08΄08˝ | 139˚08΄09˝ | 178˚24΄23˝ | 178˚24΄27˝ | 121˚54΄39˝ | 121˚54΄37˝ | |
| 53˚53΄53˝ | 53˚53΄55˝ | 231˚48΄47˝ | 231˚48΄50˝ | 232˚38΄09˝ | 232˚38΄06˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 216˚16΄16˝ | 216˚16΄18˝ | 217˚17΄17˝ | 217˚17΄12˝ | 218˚18΄18˝ | 218˚18΄19˝ | |
| 201˚29΄27˝ | 201˚29΄21˝ | 179˚56΄03˝ | 179˚56΄58˝ | 151˚26΄09˝ | 151˚26΄02˝ | |
| 156˚24΄38˝ | 156˚24΄35˝ | 129˚24΄43˝ | 129˚24΄46˝ | 203˚31΄56˝ | 203˚31΄51˝ | |
| 97˚53΄08˝ | 97˚53΄02˝ | 168˚37΄05˝ | 168˚37΄06˝ | 76˚48΄24˝ | 76˚48΄27˝ | |
| 128˚46΄12˝ | 128˚46΄07˝ | 143˚06΄16˝ | 143˚06΄11˝ | 165˚56΄04˝ | 165˚56΄59˝ | |
| 181˚37΄59˝ | 181˚37΄01˝ | 98˚22΄39˝ | 98˚22΄36˝ | 133˚33΄29˝ | 133˚33΄26˝ | |
| 176˚13΄39˝ | 176˚13΄35˝ | 136˚09΄54˝ | 136˚09΄50˝ | 221˚08΄38˝ | 221˚08΄41˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 119˚19΄19˝ | 119˚19΄22˝ | 200˚20΄20˝ | 200˚20΄11˝ | 221˚21΄21˝ | 221˚21΄24˝ | |
| 168˚53΄35˝ | 168˚53΄29˝ | 211˚56΄59˝ | 211˚57΄02˝ | 198˚58΄02˝ | 198˚57΄56˝ | |
| 154˚37΄09˝ | 154˚37΄02˝ | 98˚44΄37˝ | 98˚44΄31˝ | 77˚39΄17˝ | 77˚39΄12˝ | |
| 93˚06΄21˝ | 93˚06΄16˝ | 144˚39΄02˝ | 144˚38΄56˝ | 165˚47΄39˝ | 165˚47΄36˝ | |
| 127˚24΄59˝ | 127˚25΄02˝ | 176˚06΄21˝ | 176˚06΄24˝ | 179˚06΄18˝ | 179˚07΄20˝ | |
| 211˚48΄54˝ | 211˚48΄50˝ | 79˚18΄17˝ | 79˚18΄15˝ | 200˚12΄44˝ | 200˚12΄40˝ | |
| 206˚36΄00˝ | 206˚36΄54˝ | 125˚51΄36˝ | 125˚51΄33˝ | 131˚43΄56˝ | 131˚43΄53˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 122˚22΄22˝ | 122˚22΄16˝ | 123˚23΄23˝ | 123˚23΄19˝ | 124˚24΄24˝ | 124˚24΄22˝ | |
| 136˚59΄02˝ | 136˚58΄59˝ | 98˚58΄17˝ | 98˚58΄12˝ | 89˚36΄08˝ | 89˚36΄11˝ | |
| 94˚47΄38˝ | 94˚47΄31˝ | 246˚39΄04˝ | 246˚39΄07˝ | 133˚57΄31˝ | 133˚57΄26˝ | |
| 157˚03΄59˝ | 157˚04΄02˝ | 181˚42΄52˝ | 181˚42΄53˝ | 178˚41΄42˝ | 178˚41΄35˝ | |
| 219˚16΄17˝ | 219˚16΄14˝ | 167˚06΄36˝ | 167˚06΄30˝ | 216˚00΄59˝ | 216˚01΄03˝ | |
| 86˚05΄44˝ | 86˚05΄40˝ | 152˚37΄08˝ | 152˚37΄04˝ | 67˚15΄28˝ | 67˚15΄34˝ | |
| 181˚32΄06˝ | 181˚32΄01˝ | 78˚15΄57˝ | 78˚15΄54˝ | 141˚53΄16˝ | 141˚53΄13˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 225˚25΄25˝ | 225˚25΄20˝ | 126˚26΄26˝ | 126˚26΄20˝ | 127˚27΄27˝ | 127˚27΄30˝ | |
| 101˚54΄13˝ | 101˚54΄16˝ | 141˚41΄37˝ | 141˚41΄40˝ | 131˚35΄59˝ | 131˚36΄02˝ | |
| 176˚29΄08˝ | 176˚29΄02˝ | 99˚59΄58˝ | 100˚00΄03˝ | 97˚51΄08˝ | 97˚51΄03˝ | |
| 93˚44΄59˝ | 93˚44΄57˝ | 231˚38΄05˝ | 231˚37΄58˝ | 154˚44΄22˝ | 154˚44΄18˝ | |
| 125˚01΄37˝ | 125˚01΄42˝ | 175˚05΄16˝ | 175˚05΄12˝ | 79˚06΄34˝ | 79˚06΄31˝ | |
| 213˚35΄27˝ | 213˚35΄20˝ | 153˚12΄34˝ | 153˚12΄32˝ | 168˚18΄37˝ | 168˚18΄32˝ | |
| 154˚57΄59˝ | 154˚57΄55˝ | 168˚44΄19˝ | 168˚44΄15˝ | 235˚42΄11˝ | 235˚42΄07˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 122˚22΄12˝ | 122˚22΄16˝ | 123˚23΄23˝ | 123˚23΄19˝ | 124˚24΄24˝ | 124˚24΄22˝ | |
| 136˚59΄02˝ | 136˚58΄59˝ | 98˚58΄17˝ | 98˚58΄12˝ | 89˚36΄08˝ | 89˚36΄11˝ | |
| 94˚47΄38˝ | 94˚47΄31˝ | 246˚39΄04˝ | 246˚39΄07˝ | 133˚57΄31˝ | 133˚57΄26˝ | |
| 157˚03΄59˝ | 157˚04΄02˝ | 181˚42΄52˝ | 181˚42΄53˝ | 178˚41΄42˝ | 178˚41΄35˝ | |
| 219˚16΄17˝ | 219˚16΄14˝ | 167˚06΄36˝ | 167˚06΄30˝ | 216˚00΄59˝ | 216˚01΄03˝ | |
| 86˚05΄44˝ | 86˚05΄40˝ | 152˚37΄08˝ | 152˚37΄04˝ | 67˚15΄28˝ | 67˚15΄34˝ | |
| 181˚32΄06˝ | 181˚32΄01˝ | 78˚15΄57˝ | 78˚15΄54˝ | 141˚53΄16˝ | 141˚53΄13˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 93˚08΄08˝ | 93˚08΄01˝ | 261˚51΄58˝ | 261˚51΄54˝ | 162˚24΄25˝ | 162˚24΄29˝ | |
| 125˚21΄59˝ | 125˚21΄56˝ | 143˚24΄26˝ | 143˚24΄28˝ | 176˚13΄13˝ | 176˚13΄12˝ | |
| 198˚29΄34˝ | 198˚29΄40˝ | 71˚32΄59˝ | 71˚32΄02˝ | 79˚59΄58˝ | 79˚59΄50˝ | |
| 235˚11΄21˝ | 235˚11΄23˝ | 238˚18΄04˝ | 238˚18΄00˝ | 161˚36΄42˝ | 161˚36΄38˝ | |
| 79˚59΄59˝ | 79˚59΄02˝ | 196˚51΄49˝ | 196˚51΄42˝ | 203˚48΄03˝ | 203˚48΄07˝ | |
| 135˚35΄41˝ | 135˚35΄36˝ | 178˚34΄29˝ | 178˚34΄21˝ | 154˚46΄28˝ | 154˚46΄20˝ | |
| 154˚47΄39˝ | 154˚47΄36˝ | 217˚17΄17˝ | 217˚17΄12˝ | 265˚15΄15˝ | 265˚15΄20˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 154˚54΄54˝ | 154˚54΄50˝ | 211˚11΄11˝ | 211˚11΄09˝ | 212˚12΄12˝ | 212˚12΄06˝ | |
| 79˚09΄27˝ | 79˚09΄22˝ | 193˚24΄24˝ | 193˚24΄29˝ | 139˚51΄24˝ | 139˚51΄28˝ | |
| 161˚12΄35˝ | 161˚12΄00˝ | 77˚53΄08˝ | 77˚53΄02˝ | 87˚37΄59˝ | 87˚37΄52˝ | |
| 183˚37΄29˝ | 183˚37΄25˝ | 161˚48΄37˝ | 161˚48΄31˝ | 161˚24΄02˝ | 161˚24΄59˝ | |
| 98˚36΄05˝ | 98˚36΄02˝ | 159˚07΄27˝ | 159˚07΄25˝ | 203˚03΄34˝ | 203˚03΄36˝ | |
| 213˚23΄48˝ | 213˚23΄53˝ | 232˚34΄58˝ | 232˚34΄55˝ | 181˚17΄16˝ | 181˚17΄13˝ | |
| 254˚18΄02˝ | 254˚18΄56˝ | 181˚54΄59˝ | 181˚54΄56˝ | 152˚36΄37˝ | 152˚36΄00˝ | |
| № изм | Варианты | |||||
| L’ | L’’ | L’ | L’’ | L’ | L’’ | |
| 119˚19΄19˝ | 119˚19΄22˝ | 200˚20΄20˝ | 200˚20΄11˝ | 221˚21΄21˝ | 221˚21΄24˝ | |
| 168˚53΄35˝ | 168˚53΄29˝ | 211˚56΄59˝ | 211˚57΄02˝ | 198˚58΄02˝ | 198˚57΄56˝ | |
| 154˚37΄09˝ | 154˚37΄02˝ | 98˚44΄37˝ | 98˚44΄31˝ | 77˚39΄17˝ | 77˚39΄12˝ | |
| 93˚06΄21˝ | 93˚06΄16˝ | 144˚39΄02˝ | 144˚38΄56˝ | 165˚47΄39˝ | 165˚47΄36˝ | |
| 127˚24΄59˝ | 127˚25΄02˝ | 176˚06΄21˝ | 176˚06΄24˝ | 179˚06΄18˝ | 179˚07΄20˝ | |
| 211˚48΄54˝ | 211˚48΄50˝ | 79˚18΄17˝ | 79˚18΄15˝ | 200˚12΄44˝ | 200˚12΄40˝ | |
| 206˚36΄00˝ | 206˚36΄54˝ | 125˚51΄36˝ | 125˚51΄33˝ | 131˚43΄56˝ | 131˚43΄53˝ |
Задача 4
Произвести обработку результатов ряда неравноточных измерений. Найти среднюю весовую и среднюю квадратическую погрешность средневесового значения.
| № измерен | Варианты | Ср.кв. погреш. | ||||||||
| 121°35΄43˝ | 137°21΄34˝ | 151°51΄13˝ | 237°49΄24˝ | 150°56΄07˝ | 98°11΄12˝ | 5˝ | ||||
| 121°35΄49˝ | 31˝ | 15˝ | 26˝ | 08˝ | 08˝ | 10˝ | ||||
| 121°35΄41˝ | 33˝ | 18˝ | 20˝ | 09˝ | 06˝ | 5˝ | ||||
| 121°35΄47˝ | 39˝ | 19˝ | 19˝ | 05˝ | 14˝ | 10˝ | ||||
| 121°35΄40˝ | 37˝ | 14˝ | 30˝ | 07˝ | 13˝ | 2˝ | ||||
| 121°35΄38˝ | 30˝ | 17˝ | 27˝ | 12˝ | 14˝ | 2˝ | ||||
| 121°35΄48˝ | 39˝ | 20˝ | 25˝ | 06˝ | 09˝ | 5˝ | ||||
| 121°35΄46˝ | 31˝ | 14˝ | 21˝ | 13˝ | 12˝ | 5˝ | ||||
| 121°35΄45˝ | 36˝ | 17˝ | 23˝ | 15˝ | 16˝ | 10˝ | ||||
| 121°35΄43˝ | 34˝ | 15˝ | 28˝ | 07˝ | 17˝ | 2˝ | ||||
| № измерен | Варианты | Ср.кв. погреш. | ||||||||
Популярное: Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы... Как распознать напряжение: Говоря о мышечном напряжении, мы в первую очередь имеем в виду мускулы, прикрепленные к костям ... Как выбрать специалиста по управлению гостиницей: Понятно, что управление гостиницей невозможно без специальных знаний. Соответственно, важна квалификация...  ©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (1576)
|
Почему 1285321 студент выбрали МегаОбучалку... Система поиска информации Мобильная версия сайта Удобная навигация Нет шокирующей рекламы |
(0.007 сек.)

