Тема 4.4 Операции над множествами

 

Из элементов двух множеств можно образовывать новые множества. Пусть даны два множества: А={2,4,6,8} и B={5,6,7,8,9}.Образуем множество С, в которое включим общие элементы множеств А и В, т.е. С={6,8}. Так полученное множество С называют пересечением множествА и В.

Определение.Пересечением множеств А и В называют множество содержащее все элементы, которые принадлежат множеству А и множеству В.

Пересечение множеств А и В обозначают . Таким образом по определению получаем

Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область.

В

В том случае, когда множества А и В не имеют общих элементов говорят, что их пересечение пусто и пишут: = .

А

 

 

Рис.14

Пусть даны два множества А={2,4,6,8} и B={5,6,7,8,9}. Образуем множество D, в которое включим элементы, принадлежащие хотя бы одному из данных множеств, т.е. множеству А или множеству В: D={2,4,6,8,5,7,9}. Так полученное множество D называют объединением множеств А и В.

Определение.Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.

Объединение множеств А и В обозначают . Таким образом, по определению, ={x │x .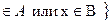

Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью. А В

 

Рис.15

 

Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.

Определение.Разностью множеств А и В называется множество , содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В.

Разность множеств А и В обозначают А\В. Тогда, по определению, имеем :

Если изобразить множества А и В при помощи кругов Эйлера, то разность А\В изобразится заштрихованной областью.

 

В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого , при этом разность

А В

 

 

Рис.16

 

множеств А\В называют дополнением множества В до множества А , и обозначают символом В^/_А, а наглядно изображают так, как представлено на рисунке.

 

 

Определение.Пусть . Дополнением множества В до множества А, называется множество, содержащее все элементы множества А, которые не принадлежат множеству В. Как уже было сказано, в случае когда , А\В= В/А.

А

 

	В/А

 

 

Рис.17

Из определения следует, что В^/_А=

Пример. Найти разность множеств А и В, если

А={1,2,3,4,5,6} , B={2,4,6,8,10}.

Решение :

А\В={1,3,5} , B\A={8,10}.

 

Упражнения:

1. Укажите характеристическое свойство элементов множества:

а) {а,е,ё,и,о,у,э,я,ю,ы};

б)

2.Изобразите на координатной прямой множество решений неравенства если х- действительное число:

а) x>5; б) -4,5≤x≤4; в) x≤-3,8.

3.Изобразите с помощью кругов Эйлера отношения между множествами C u D, если:

а) С- множество двузначных чисел,

D=

б) С-множество двузначных чисел,

D- множество натуральных чисел, не меньших 10.

4. Известно, что х 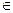А. следует ли из этого, что ?

5. Найдите пересечение множеств А и В, если:

А= 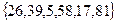, В=

6. начертите два треугольника так, чтобы их пересечением:

а) был треугольник, б) был отрезок, в) была точка.

7. Найдите объединение множеств:

а) , .

8. Используя координатную прямую, найдите объединение множеств решений неравенств, в которых х- действительное число:

а) x>-2 и x>0; б) x≥5 и x<-7,5; в) -7≤x≤5.

9. Найдите разность множеств А и В, если:

а)

б)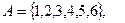

В= .