 |
Главная |
Смешанное произведение в координатной форме
|
из
5.00
|
Лекция 2. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Определение.Три некомпланарных вектора 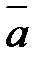 ,
,  и
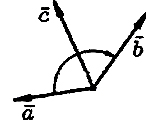
и 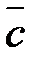 , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 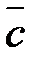 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 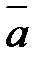 ко второму вектору
ко второму вектору  виден совершающимся против часовой стрелки, и левую, если по часовой.
виден совершающимся против часовой стрелки, и левую, если по часовой.

| 
|
| правая тройка | левая тройка |
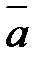 на вектор
на вектор  называется вектор
называется вектор 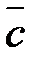 , который:
, который:
1) 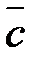 ^
^ 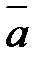 и
и 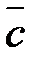 ^
^  ;
;
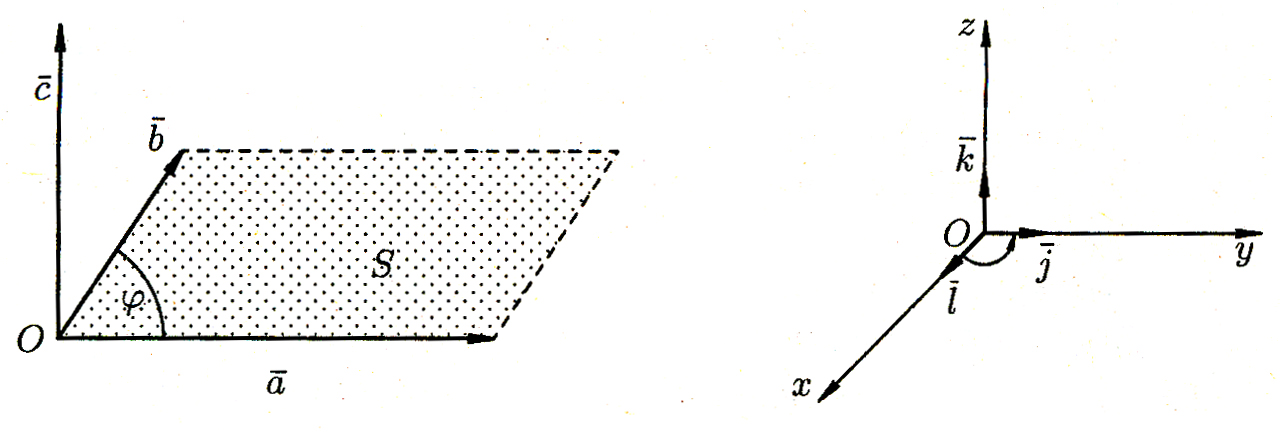
2) имеет длину, численно равную площади параллелограмма, построенного на векторах 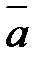 и
и  как на сторонах, т. е.
как на сторонах, т. е.
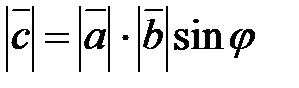 , где
, где  ;
;
3) тройка векторов 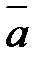 ,
,  и
и 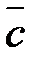 правая.
правая.
Векторное произведение обозначается 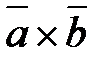 или
или  .
.
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами 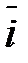 ,
, 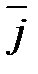 и
и 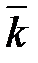 :
:
 ,
, 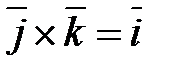 ,
,  .
.
Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак,
т. е. 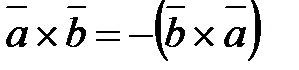 .
.
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя,
т. е.  .
.
3. Два ненулевых вектора 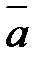 и
и  коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е.  .
.
В частности, 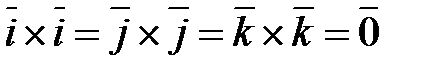 .
.
4. Векторное произведение обладает распределительным свойством:
 .
.
Примем без доказательства.
Векторное произведение в координатной форме
Пусть заданы два вектора 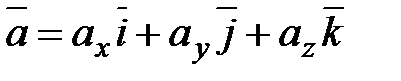 и
и 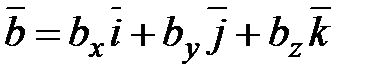 . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
. Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
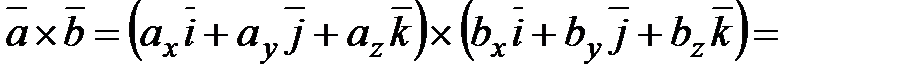
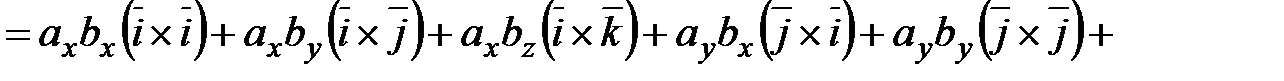
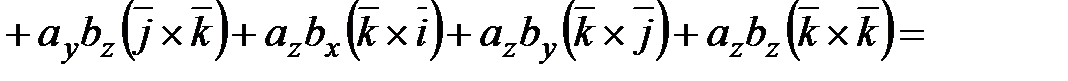
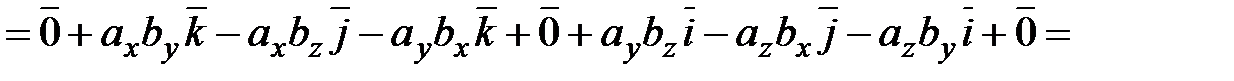

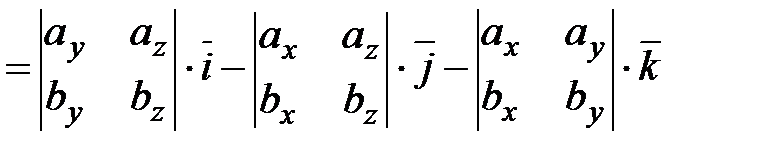 ,
,
т. е.

Полученную формулу можно записать еще короче:
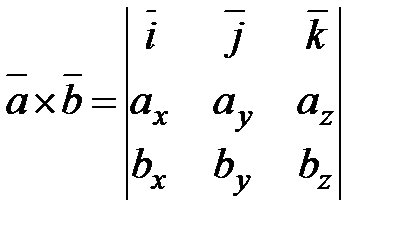 .
.
Пример.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Определение.Произведение векторов  ,
,  и
и 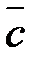 , составленное следующим образом:
, составленное следующим образом:  , называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
, называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Теорема. Смешанное произведение трех векторов равно 
где V – объем параллелепипеда, построенного на векторах 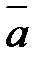 ,
,  и
и 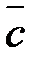 .
.
Свойства смешанного произведения
1. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е.  .
.
Действительно, 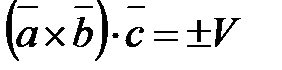 и
и 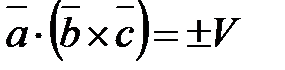 . Знак в правой части этих равенств берем один и тот же, так как тройки векторов
. Знак в правой части этих равенств берем один и тот же, так как тройки векторов  и
и 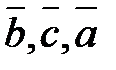 — одной ориентации.
— одной ориентации.
Следовательно, 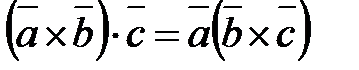 . Это позволяет записывать смешанное произведение векторов
. Это позволяет записывать смешанное произведение векторов 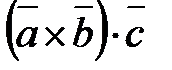 в виде
в виде 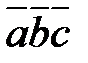 без знаков векторного, скалярного умножения.
без знаков векторного, скалярного умножения.
2. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. 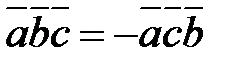 ,
,  ,
, 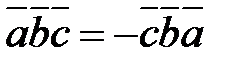 .
.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
Смешанное произведение в координатной форме
Пусть заданы векторы 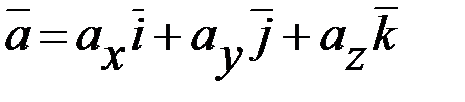 ,
,  ,
,  . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
. Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
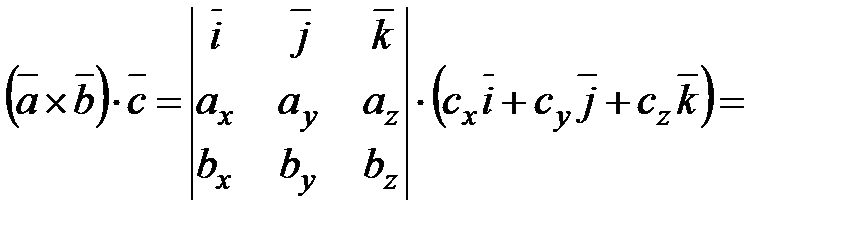
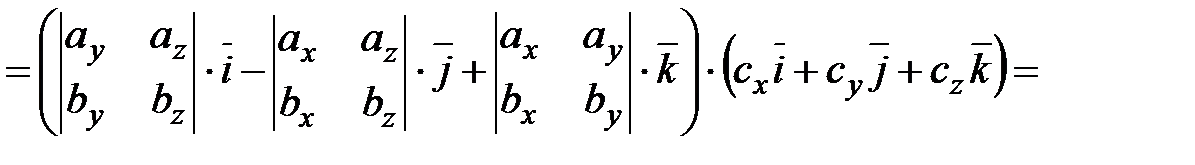
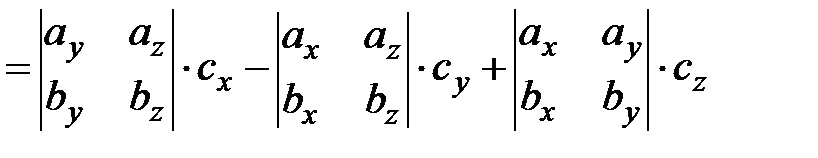 .
.
Полученную формулу можно записать короче:
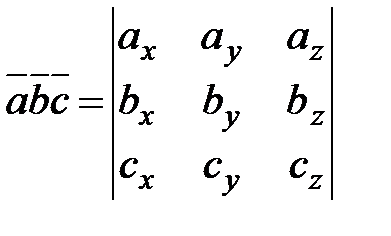 .
.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
|
из
5.00
|
Обсуждение в статье: Смешанное произведение в координатной форме |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

