 |
Главная |
Проектирование дискретных систем
|
из
5.00
|
КИХ фильтры.
1. Передаточная функция фильтра с конечной импульсной характеристикой (КИХ) записывается как:
| а | H(z) = 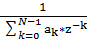
|
| б | H(z) = 
|
| в | H(z) = 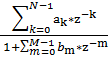
|
2. Фазовая характеристика (ФЧХ) КИХ фильтра линейно зависит от частоты при условии:
| а | 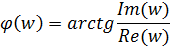
|
| б | 
|
| в | 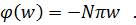
|
3. Для того, чтобы ФЧХ фильтра была линейной, необходимо, чтобы отсчеты импульсной характеристики КИХ фильтра были:
| а | монотонно убывающими |
| б | иметь колебательный характер от 0 до N-1 |
| в | иметь любой вид симметрии от 0 до N-1 значений отсчетов относительно ее среднего значения  или или 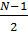
|
4. Какой метод проектирования КИХ фильтров наиболее прост в применении
| а | метод умножения значений импульсной характеристики на отсчеты вспомогательной временной функции |
| б | метод сложения значений импульсной характеристики со значениями вспомогательной временной функции |
| в | метод временной свертки импульсной характеристики и вспомогательной временной функции |
5. В каких случаях для расчета КИХ фильтра наиболее приемлем метод частотных выборок:
| а | для расчета любых фильтров |
| б | для расчета только ФНЧ |
| в | для расчета только ФВЧ |
| г | для расчета узкополосных фильтров любого типа |
| д | для расчета полосовых и режекторных фильтров |
6. Какой метод позволяет оптимизировать процесс проектирования КИХ фильтра:
| а | метод взвешивания |
| б | метод наименьших квадратов |
| в | метод наилучшей равномерной аппроксимации |
| г | метод частотных выборок |
Проектирование дискретных систем.
БИХ фильтры.
1. Какой метод решения аппроксимационной задачи наиболее часто используется при проектировании БИХ фильтра:
| а | метод преобразования аналоговых фильтров в цифровые |
| б | метод взвешивания (временных окон) |
| в | метод средних квадратов |
| г | метод частотных выборок |
2. На чем основан метод билинейного преобразования:
| а | конформное отображение точек частотной плоскости S в точки Z-плоскости |
| б | замена переменной Z на функцию 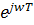 , т.е. , т.е. 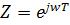
|
| в | замена переменной 
|
| г | замена переменной 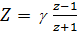
|
| д | замена переменной 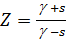
|
3. При билинейном преобразовании частотных характеристик происходит следующее:
| а | полюсы аналогового фильтра из правой полуплоскости S переходят в левую полуплоскость Z |
| б | полюсы аналогового фильтра из левой полуплоскости S переходят внутрь единичной окружности Z плоскости |
| в | полюсы аналогового фильтра из левой полуплоскости S переходят в плоскость Z за единичной окружностью |
4. При билинейном преобразовании частотных характеристик аналогового фильтра в частотные характеристики цифровых фильтров происходит:
| а | линейное преобразование частотной оси 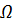 в частотную ось ω в частотную ось ω
|
| б | линейное преобразование частотной оси 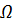 в частотную ось ω только в интервале 0 в частотную ось ω только в интервале 0 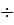 1, а далее нелинейное преобразование 1, а далее нелинейное преобразование
|
| в | нелинейное преобразование частотной оси 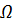 в частотную ось ω по закону в частотную ось ω по закону 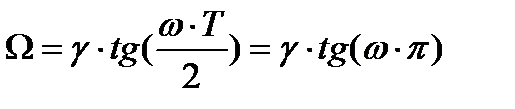 , где ω= , где ω= 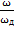
|
5. Обобщенное билинейное преобразование Константинидиса АЧХ позволяет преобразовать аналоговый фильтр ФНЧ в :
| а | цифровые фильтры ФНЧ и ФВЧ |
| б | цифровые фильтры полосовые и режекторные |
| в | цифровые избирательные фильтры любого вида (ФНЧ, ФВЧ, ПФ, РФ) |
6. Метод инвариантности импульсных характеристик аналоговых и цифровых фильтров требует:
| а | дискретизации импульсных характеристик аналоговых фильтров с шагом t=nT |
| б | ограничения длины импульсной характеристики цифрового фильтра |
| в | ограничения длины импульсной характеристики аналогового фильтра |
| г | обязательной проверки получившегося цифрового фильтра на устойчивость |
|
из
5.00
|
Обсуждение в статье: Проектирование дискретных систем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

