 |
Главная |
Асимптоты графика функции. При исследовании функций часто бывает, что при удалении координаты х точки кривой в
|
из
5.00
|
Ответ:
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
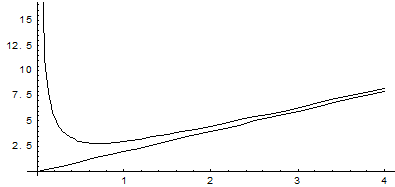
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.
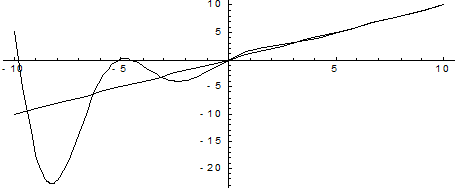
Рассмотрим подробнее методы нахождения асимптот кривых.
Вертикальные асимптоты.
Из определения асимптоты следует, что если 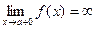 или
или  или
или  , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x).
Например, для функции 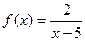 прямая х = 5 является вертикальной асимптотой.
прямая х = 5 является вертикальной асимптотой.
Наклонные асимптоты.
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.


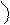
 M
M
 |
j
N
j P
Q
Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N.
Тогда MQ = y – ордината точки кривой, NQ =  - ордината точки N на асимптоте.
- ордината точки N на асимптоте.
По условию:  , ÐNMP = j,
, ÐNMP = j,  .
.
Угол j - постоянный и не равный 900, тогда


Тогда  .
.
Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
В полученном выражении выносим за скобки х:
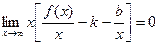
Т.к. х®¥, то 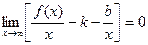 , т.к. b = const, то
, т.к. b = const, то  .
.
Тогда 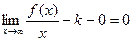 , следовательно,
, следовательно,
 .
.
Т.к. 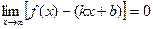 , то
, то  , следовательно,
, следовательно,

Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.
Интегрирование. Первообразная функции и её свойства.
Ответ:
Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Определение: Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 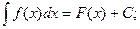
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
|
из
5.00
|
Обсуждение в статье: Асимптоты графика функции. При исследовании функций часто бывает, что при удалении координаты х точки кривой в |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

