 |
Главная |
Пример решения задач по теме
|
из
5.00
|
«Экспериментально-статистические методы обработки результатов эксперимента»
Задание 1. Расчет оценок математического ожидания, дисперсии и среднеквадратичного отклонения.
При оценке качества нагрева металла в нагревательных печах листопрокатного стана получены следующие данные по температуре поверхности заготовок после черновой группы стана (0С):
| № п/п | Вариант 1 |
Необходимо определить статистические характеристики mx*, Dx*,  x*.
x*.
Решение (вариант 1).
Найдем оценку математического ожидания для случайной величины Х – температуры поверхности заготовок:
 Вспомогательные расчеты, необходимые для вычисления оценки дисперсии случайной величины Х приведены в таблице:
Вспомогательные расчеты, необходимые для вычисления оценки дисперсии случайной величины Х приведены в таблице:
| № п/п | Xi - mx* | (Xi - mx*)2 |
| 2,2 | 4,84 | |
| 7,2 | 51,84 | |
| 17,2 | 295,84 | |
| -12,8 | 163,84 | |
| -27,8 | 772,84 | |
| 3,2 | 10,24 | |
| 12,2 | 148,84 | |
| 4,2 | 17,64 | |
| -7,8 | 60,84 | |
| 2,2 | 4,84 | |
| Σ | 1531,60 |

Среднеквадратичное отклонение температуры раската будет равно:
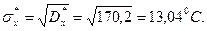
Задание 2. Расчет ошибки опыта и доверительного интервала.
Результаты измерения содержания кислорода в продуктах сгорания на выходе из методической печи дают следующие значения (%):
| № п/п | Вариант 1 |
| 4,26 | |
| 3,70 | |
| 3,90 | |
| 4,15 | |
| 3,65 | |
| 4,05 | |
| 3,96 | |
| 3,78 | |
| 3,62 |
Определить ошибку опыта и доверительный интервал с вероятностью Р=0,95.
Решение (вариант 1).
 %.
%.
 (%)2.
(%)2.
 x*=0,227%.
x*=0,227%.
Ошибка опыта для Emx будет равна
Emx=tT0,227/3.
Значение критерия Стьюдента tT=2,31 находим из таблицы для f=N-1=8; q=5%.
Значит Emx=2,31·0,227/3=0,175%.
Истинное значение математического ожидания с вероятностью 95% находится в доверительном интервале 3,897±0,175%, или 3,7225≤3,897≤4,0725. Доверительный интервал для дисперсии переменной вычисляется по формуле
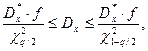
где Dx – дисперсия переменной Х;
f – число степеней свободы;
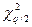 - значение
- значение  - распределения для q/2 уровня значимости;
- распределения для q/2 уровня значимости;
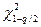 - значение
- значение  - распределения для 1-q/2 уровня значимости.
- распределения для 1-q/2 уровня значимости.
Задание 3. Выявление наличия корреляционной зависимости между случайными величинами.
Были проведены семь опытов по изучению процесса обжига извести в печи с кипящим слоем при определенной температуре. При этом факторами приняты: время контакта материала с греющей средой (с) – Х1; соотношение расходов воздуха и материала (г/г) – Х2. В качестве переменной состояния – выход обожженной извести (%). Результаты эксперимента приведены в таблице:
| № варианта | № п/п | Х1 | Х2 | Y |
| 0,68 | 50,0 | |||
| 0,65 | 30,9 | |||
| 0,43 | 36,7 | |||
| 0,45 | 37,0 | |||
| 0,46 | 20,5 | |||
| 0,45 | 17,3 | |||
| 0,42 | 51,0 |
Требуется определить коэффициенты корреляции между факторами и между факторами и переменной состояния, т.е. коэффициенты  ; оценить значимость полученных значений коэффициентов корреляции по критерию Стьюдента.
; оценить значимость полученных значений коэффициентов корреляции по критерию Стьюдента.
Решение (вариант 1).
Исходные данные и результаты предварительных вычислений сведены в таблицу:
| № п/п | Х1 | Х2 | Y | X12 | X22 | X1X2 | X1Y | X2Y | Y2 |
| 0,68 | 50,0 | 0,4624 | 21,76 | 34,00 | |||||
| 0,65 | 30,9 | 0,4225 | 63,05 | 20,085 | 297,3 | 954,81 | |||
| 0,43 | 36,7 | 0,1849 | 36,56 | 15,781 | 3119,5 | 1346,89 | |||
| 0,45 | 37,0 | 0,2025 | 44,10 | 16,65 | 1369,0 | ||||
| 0,46 | 20,5 | 0,2116 | 69,00 | 9,43 | 420,25 | ||||
| 0,45 | 17,3 | 0,2025 | 69,75 | 7,785 | 2681,5 | 299,29 | |||
| 0,42 | 51,0 | 0,1746 | 58,38 | 21,42 | |||||
| Σ | 3,54 | 243,4 | 1,8628 | 362,59 | 125,15 | 24188,3 | 9491,2 |
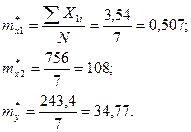


где U=1,2,3,…,N;
i=1,2,3,…,n;
j=1,2,3,…,m;
N – число опытов;
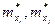 - оценки математических ожиданий каждого фактора;
- оценки математических ожиданий каждого фактора;
 - оценки среднеквадратичных отклонений.
- оценки среднеквадратичных отклонений.


Определяем расчетное значение критерия Стьюдента для каждой переменной:

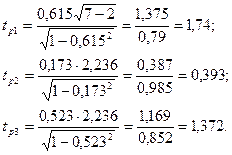
Табличное значение критерия Стьюдента определяем для f=N-2=5; q=0,05 по таблице.
tТ=2,57.
Поскольку все расчетные значения критерия Стьюдента меньше табличного, то это позволяет сделать вывод:
Корреляционной связи между случайными переменными Х1, Х2 и Y нет, т.е. они статистически независимы.
Задание 4. Практическая реализация полного факторного эксперимента.
Задача 1.
Целью эксперимента является определение зависимости скорости нагрева металла в мартеновской печи y(  ) от величины абсолютного избытка воздуха
) от величины абсолютного избытка воздуха  и тепловой нагрузки
и тепловой нагрузки 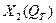 в период чистого кипения.
в период чистого кипения.
Уровни варьирования факторов.
| Уровни | Факторы | |
 , , 
| 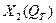 , МВт , МВт
| |
| Основной Нижний Верхний Интервал варьирования | 7*  4*
4*  10*
10*  3*
3* 
| 33,5*  30*
30*  37*
37*  3,5*
3,5* 
|
Вариант 1.
Карта проведения эксперимента
| № опыта | Порядок реализации опытов по рандомизации (две серии) | Матрица планирования | Выход y, °С/ч | ||||

| 
| 
| 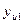
| 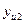
| 
| ||
| 2; 3 3; 1 4; 4 1; 2 | -1 +1 -1 +1 | -1 -1 +1 +1 | +1 -1 -1 +1 |
Решение задачи 1 (вариант 1).
- Рассчитывают построчные средние

где γ – чило повторных опытов:
 .
.
Результаты расчета заносятся в столбец  карты проведения эксперимента.
карты проведения эксперимента.
- Определяют построчные дисперсии (дисперсии воспроизводимости)

Сумма построчных дисперсий:

- Проверяют воспроизводимость опытов по критерию Кохрена:

где 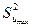 - максимальная из построчных дисперсий.
- максимальная из построчных дисперсий.
Опыты равноточны, если G< 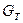 , где
, где 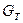 - табличные значения критерия Кохрена, выбираемое в зависимости от N, γ и уровня значимости (надежности). Для данного случая при N=4, γ=2, p=0,95 табличное значение
- табличные значения критерия Кохрена, выбираемое в зависимости от N, γ и уровня значимости (надежности). Для данного случая при N=4, γ=2, p=0,95 табличное значение 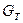 =0,906, т.е.
=0,906, т.е.
G< 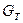 .
.
В случае неравноточности опытов необходимо увеличить число повторных экспериментов или повысить их точность.
4. Определяют коэффициенты уравнения регрессии по формулам:

- Проверяют значимость коэффициентов регрессии. Для этого определяют дисперсию эксперимента:

а также усредненную дисперсию эксперимента с учетом повторных опытов

Определяют ошибку и среднюю квадратичную ошибку коэффициенто регрессии  и
и 
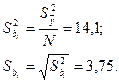
Находят значение доверительного интервала для коэффициентов регрессии
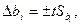
где t – табличное значение критерия Стьюдента, выбираемое в зависимости от числа степеней свободы  и выбранного уровня значимости (обычно 0,05).
и выбранного уровня значимости (обычно 0,05).
Коэффициент значим, если его абсолютное значение больше доверительного интервала, т.е. коэффициент должен бать больше ошибки его определения, взятой с определенным запасом.
В данном примере при 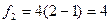 значение критерия Стьюдента t=2,78.
значение критерия Стьюдента t=2,78.
Значение доверительного интервала 
Сравнивают полученные коэффициенты с доверительным интервалом:
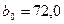 - значим
- значим
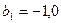 - незначим
- незначим
 - значим
- значим
 - значим
- значим
Т.о. один из коэффициентов регрессии оказался незначим и окончательно уравнение регрессии запишется в виде 
При необходимости перехода от кодированных переменных к натуральным следует подставить в полученное уравнение соответствующие соотношения связи между этими переменными.
- Проверяют адекватность (пригодность) модели, т.е. насколько хорошо полученное уравнение описывает результаты эксперимента в исследуемой области.
Для этого чаще всего применяют критерий Фишера:

где  - усредненная дисперсия эксперимента;
- усредненная дисперсия эксперимента;
 - дисперсия адекватности или остаточная дисперсия
- дисперсия адекватности или остаточная дисперсия
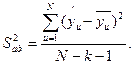
здесь  - рассчитанные полученному уравнению значения выхода при значениях кодированных переменных, соответствующих каждой из строк матрицы планирования.
- рассчитанные полученному уравнению значения выхода при значениях кодированных переменных, соответствующих каждой из строк матрицы планирования.
 - усредненное значение выхода, полученное при реализации повторных опытов для соответствующей строки.
- усредненное значение выхода, полученное при реализации повторных опытов для соответствующей строки.
Модель можно считать адекватной, если F<Fтабл. Табличное значение критерия Фишера находят в зависимости от числа степеней свободы  и
и  , где
, где
N – число вариантов опытов(строк) в матрице планирования;
K – число варьируемых факторов;
γ – число повторных опытов.
В данном примере для определения  вычислим сначала значения выхода, предсказываемые полученным выше уравнением регрессии:
вычислим сначала значения выхода, предсказываемые полученным выше уравнением регрессии:
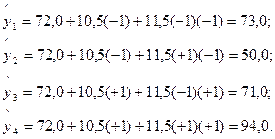
 - посчитаны выше.
- посчитаны выше.
Получим 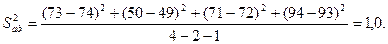
Ранее получено значение 
Вычисляем значение критерия Фишера F=1,0/56,5=0,02.
Fтабл=7,7 при 
F<Fтабл, т.е. имеются основания сделать вывод об адекватности полученной модели.
|
из
5.00
|
Обсуждение в статье: Пример решения задач по теме |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

