 |
Главная |
Метод половинного деления
|
из
5.00
|
Домашняя лабораторная работа по теме «Приближенное решение уравнений с одной переменной»
Задание. Найти один из корней уравнения методом деления отрезка пополам (методом Фибоначчи, «золотого сечения», рандомизации) с точностью до 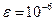 : 1) отделить корень на отрезке
: 1) отделить корень на отрезке  , проверить его единственность; 2) реализовать один из методов деления отрезка в заданном отношении (использовать ЭВМ или калькулятор); 3) сделать проверку точности найденного решения подстановкой его в исходное уравнение.
, проверить его единственность; 2) реализовать один из методов деления отрезка в заданном отношении (использовать ЭВМ или калькулятор); 3) сделать проверку точности найденного решения подстановкой его в исходное уравнение.
Порядок выполнения работы
1) Графическое отделение корня в случае достаточно сложного выражения y=f(х) можно производить следующим образом. Допустим, что уравнение можно представить в виде f1(x) = f2(x). В этом случае строим графики функций у=f1(x) и y=f2(x); абсциссы точек пересечения кривых будут действительными корнями уравнения. Найдем, например, приближенно корни уравнения x-sin x-1 = 0, записав это уравнение в виде x-1 = sin x. Построим графики функций y = sin x и у = х-1 (рис.2). Точка пересечения этих линий имеет абсциссу х ≈ 1,9, что можно считать грубым приближением значения корня.

Рис. 2
Интервал [а;b] является интервалом изоляции корня, если его можно считать настолько малым, что на нем лежит точно один корень исходного уравнения. Выбор этого интервала производится на основании свойства непрерывных функций: если функция у=f(x) непрерывна на отрезке [а;b] и на концах отрезка принимает значения разных знаков (f(a)f(b) < 0), то между точками а и b есть хотя бы один корень уравнения f(x) = 0. Корень будет единственным, если производная f'(x) существует и сохраняет постоянный знак внутри [а;b] (рис. 3).

Рис. 3
Найдем интервал изоляции корня уравнения: х3+x2-1=0. Для этого представим уравнение в виде: х3 =1-x2, т. е. f(x)=x3 и g(x)=1-x2. Построим приближенно графики функций y=f(x) и y=g(x) (рис 4). Точка пересечения графиков двух функций, а значит, и корень уравнения находится на отрезке [0;1]. Проверим аналитические условия: f(0)=03+02-1=-1<0, f(1)= 13 +12-1=1>0, и f'(х)=3х²+2x>0 на отрезке [0;1]. Таким образом, мы определили интервал изоляции корня, для нахождения которого достаточно применить любой из аналитических методов численного решения уравнений.
у=x3

у=1-x2
Рис. 4
Задача отыскания корней уравнений может считаться практически решенной, если удалось определить корни с нужной степенью точности и указать пределы возможной погрешности.
Метод половинного деления
Рассмотрим один из самых простых численных методов решения уравнений – метод половинного деления. Пусть для уравнения  найден интервал изоляции корня – отрезок [а;b]. Для уточнения искомого корня отрезок [а;b] делим пополам и из двух, полученных в результате этого деления отрезков выбираем тот, для которого выполняются условия существования и единственности корня (на концах отрезка функция принимает значения разных знаков). Середину отрезка находим по формуле хi=(a+b)/2, i=1,2,3…, и продолжаем данный процесс пока не достигнем необходимой точности (рис.5).
найден интервал изоляции корня – отрезок [а;b]. Для уточнения искомого корня отрезок [а;b] делим пополам и из двух, полученных в результате этого деления отрезков выбираем тот, для которого выполняются условия существования и единственности корня (на концах отрезка функция принимает значения разных знаков). Середину отрезка находим по формуле хi=(a+b)/2, i=1,2,3…, и продолжаем данный процесс пока не достигнем необходимой точности (рис.5).

Рис.5
Рассмотрим применение метода половинного деления на примере решения уравнения х3+x2-1 = 0 на отрезке [0;1]. Разделим интервал изоляции пополам – это точка х=0,5. Получим два подотрезка – [0;0,5] и [0,5;1]. Вычислим значения функции на концах отрезков, f(0)=-1<0,f(0,5)=0,53+0,52-1=0,125+0,25-1=-0,625< 0, f(1)=13+12-1=1+1--1=1>0, т. е. на концах отрезка [0,5;1] функция имеет значения разных знаков, следовательно, корень уравнения принадлежит отрезку [0,5;1]. Выбираем этот отрезок для дальнейшего рассмотрения.
Повторяем метод половинного деления уже для нового отрезка. Середина отрезка x=(0,5+1)/2=0,75, и из двух полученных отрезков выбираем правый отрезок [0,75;1], т.к. f(0,75) = -0,015625< 0, f(1)=1> 0. Процесс продолжается до получения корня с заданной степенью точности.
Если делить отрезок [a;b] сразу на десять частей, то на следующем шаге можно получить отрезок в десять раз меньший, чем [a;b].
2. Метод Фибоначчи
Рассмотрим одну из разновидностей метода половинного деления – метод Фибоначчи.
Пусть дано уравнение  , где функция у=
, где функция у=  непрерывна на
непрерывна на  и
и  . Для уточнения корня данного уравнения введем последовательность чисел Фибоначчи:
. Для уточнения корня данного уравнения введем последовательность чисел Фибоначчи:  ,
,  ,
,  , это будут числа 1,1,2,3,5,8,13,21 и т.д. Согласно данному методу, на каждом
, это будут числа 1,1,2,3,5,8,13,21 и т.д. Согласно данному методу, на каждом  ом этапе отрезок делят в отношении
ом этапе отрезок делят в отношении  , где
, где 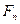 и
и  соответственно
соответственно  е и
е и  е число из последовательности Фибоначчи. Так на первом шаге отрезок
е число из последовательности Фибоначчи. Так на первом шаге отрезок  делят в отношении
делят в отношении  (пополам) и выбирают тот из них, на концах которого функция
(пополам) и выбирают тот из них, на концах которого функция  имеет разные знаки. На втором этапе выбранный суженный отрезок
имеет разные знаки. На втором этапе выбранный суженный отрезок  делят в отношении
делят в отношении 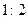 , следующие в отношениях
, следующие в отношениях  ,
,  ,
, 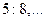 В результате получаем на некотором этапе точный корень уравнения, или же бесконечную последовательность отрезков
В результате получаем на некотором этапе точный корень уравнения, или же бесконечную последовательность отрезков  таких, что
таких, что  (n=1,2,…). Формула для вычисления имеет вид:
(n=1,2,…). Формула для вычисления имеет вид:  В качестве корня можем принять
В качестве корня можем принять  .
.
|
из
5.00
|
Обсуждение в статье: Метод половинного деления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

