Определенный интеграл

Задача о площади криволинейной трапеции.

Пусть функция 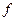определена на отрезке . Разобьем этот отрезок на части точками такими, что 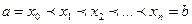. Получим разбиение 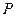, состоящее из частичных отрезков 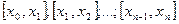На каждом частичном отрезке 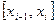длиной 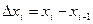выберем произвольно точку 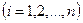и назовем такое разбиение 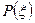, где через 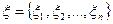обозначен набор выбранных точек , разбиением с отмеченными точками. Легко видеть, что даже для одного и того же разбиения 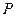, представляющего собой множество точек , можно построить бесконечно много разбиений с отмеченными точками только за счет выбора точек .

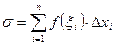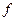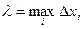Составим сумму , которую назовем интегральной суммой. Эта сумма зависит от функции , от способа разбиения отрезка на части, а также от выбора точек . Число назовем параметром разбиения 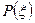. Очевидно, что одно и то же число 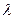может являться параметром для бесконечного множества разбиений с отмеченными точками.

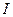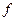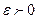Определение 3. Число назовем определенным интегралом от функции на отрезке , если для любого найдется 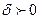такое, что для любого разбиения 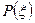с отмеченными точками с параметром 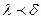будет выполняться условие .

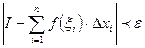Обозначение: 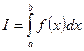. При этом 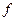называют подинтегральной функцией; 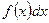- подинтегральным выражением; 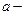нижним пределом интегрирования; 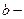верхним пределом интегрирования.

Теорема 2. Если функция 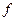интегрируема на , то она ограничена на .

Свойства определенного интеграла:

1°. Если функция 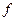интегрируема на , то функция , где 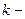число, также будет интегрируемой на , причем .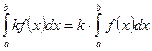

2°. Если функции 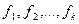интегрируемы на , то функция 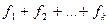. Также будет интегрируемой на , причем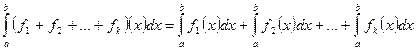

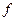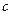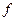3°. Если функция интегрируема на и - некоторая внутренняя точка , то функция будет интегрируема на каждом из отрезков 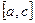и 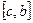, причем .

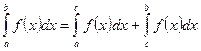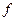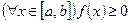4°. Если функция интегрируема на и , то .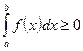

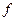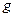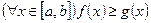5°. Если функции и интегрируемы на и , то .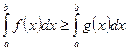

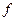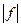6°. Если функция интегрируема на , то и функция будет интегрируема на , причем .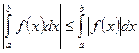

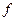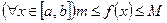7°. Если функция интегрируема на и , то .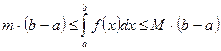

8°. Если функция 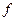интегрируема на и 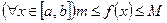, то существует такое число 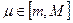, для которого справедливо равенство .

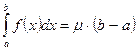9° 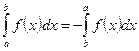. В частности если 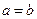, то из последнего равенства следует, что .

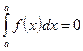Теорема 3. Если функция 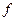интегрируема на , то функция 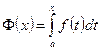будет непрерывной на .

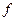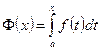Теорема 4. Если функция непрерывна на , то функция будет дифференцируемой на , причем .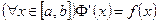

Формула Ньютона – Лейбница : .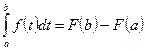

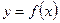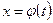Теорема 5. Пусть функция непрерывна на , а функция , определенная на 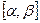, обладает следующими свойствами:

1) 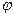имеет непрерывную производную на ;

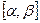2) ;

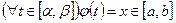3) .

Тогда .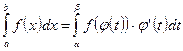

Теорема 6. Если функци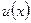и и 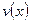имеют на непрерывные производные функции, то справедлива формула 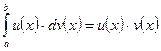| (формула интегрирования по частям в определенном интеграле).

Вычисление площадей плоских фигур с помощью определенного интеграла.