 |
Главная |
Решение типовых заданий
|
из
5.00
|
Зеленодольский филиал
Кафедра высшей математики
Т.Е. Платонова
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
По дисциплине «Основы математической
Обработки информации»
Для студентов направления подготовки
Педагогическое образование»
Квалификация (степень) выпускника
Бакалавр
Форма обучения: очная, заочная
Казань - 2015
УДК 51. (075.8)
ББК 22.18я73
П 37
Платонова Т.Е.,к.пед.н., доцент кафедры высшей математики
П 37
Методические указания и контрольные задания составлены в соответствии с требованиями ФГОС ВПО с учетом рекомендаций ООП ВПО по направлению и профилю подготовки
Педагогическое образование»
Методические указания и контрольные задания рассмотрены на заседании кафедры высшей математики
Протокол заседания № от «____» ________________ 20____ г.
Заведующий кафедрой
__________________________ /________________ /_________ /
(фамилия, имя, отчество) (ученое звание) (подпись)
СОГЛАСОВАНО
заведующий кафедрой
Шевченко Д.В. / доцент /_________ /
(фамилия, имя, отчество) (ученое звание) (подпись)
«____» _________ 20____ г.
Председатель секции естественнонаучных дисциплин
__________________________ /________________ /_________ /
(фамилия, имя, отчество) (ученое звание) (подпись)
Зав. библиотекой ___________________ /_______________/
(подпись) (ФИО)
УДК 51. (075.8)
ББК 22.18я73
© ЧОУ ВПО «Институт экономики,
управления и права (г. Казань»), 2015
© Платонова Т.Е., 2015
СОДЕРЖАНИЕ
Введение ……………………………………………………………………. 4
I. Контрольные задания по вариантам …………………………………… 5
II. Решение типовых заданий, задание 1 …………………………………14
III. Задание 2 ………………………………………………………………..18
IV. Задание 3 ………………………………………………………………..20
V. Литература …………………………………………………………….....22
VI. Приложение …………………………………………………………….25
ВВЕДЕНИЕ
Методические указания являются основным путеводителем для выполнения студентами контрольных заданий по дисциплине «Основы математической обработки информации». По каждому заданию приводится необходимый теоретический материал и алгоритм решения в соответствии с требованиями ФГОС ВПО с учетом рекомендаций ООП ВПО по направлению и профилю подготовки «Педагогическое образование». Выполнение студентами контрольных заданий данного типа послужит основой для математической обработки результатов экспериментальной работы в семестре и в дальнейшем выпускной квалификационной работе.
Методические указания предназначены студентам заочной формы обучения, но также могут быть использованы для организации работы студентов очной и дистанционной формы обучения.
Указания по выполнению контрольной работы
1. Номер варианта контрольной работы соответствует последней цифре номера студенческого билета.
2. Оформить титульный лист (Приложение 1, стр. 25).
3. Решение заданий располагать в порядке возрастания их номеров, сохраняя номер задания.
4. Перед решением каждого задания выписать полностью условие.
5. Решение каждого задания сопровождать объяснениями, формулами для расчетов и заканчивать ответом.
6. Оформление решений выполнять аккуратно, без исправлений. Отводить поля для замечаний проверяющего.
7. В работу должны быть включены все задачи, указанные в задании по своему варианту. Не допускается замена задач контрольного задания другими. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
8. Если вычисления, выполняемые при решении задач, приближенные, то следует придерживаться правил приближенных вычислений.
9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, выполнить все рекомендации рецензента, сделать соответствующие исправления и дополнения в той же тетради (после имеющихся решений и записи «Работа над ошибками»).
10. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию на кафедре. При решении заданий контрольной работы можно использовать различные методы решений.
Контрольные задания
Задание 1.
Вариант 1.
Пусть дана последовательность значений некоторого признака: 15; 20; 18; 20; 25; 11; 12; 13; 24; 23; 23; 24; 21; 22; 21; 23; 23; 22; 21; 14; 14; 22; 15; 16; 20; 20; 16; 16; 20; 17; 17; 17. Выполните статистическую обработку данных по следующей схеме:
1.выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2.составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 7);
3. построить гистограмму распределения;
4.найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 2.
Пусть дана последовательность значений некоторого признака: 44; 78; 47; 79; 54; 52; 56; 50; 56; 55; 48; 51; 66; 74; 60; 42; 60; 76; 49; 45; 69; 51; 45; 46; 59; 61; 44; 62; 70; 45; 47; 80. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2.составить равноинтервальный вариационный ряд, разбив всю вариацию на kинтервалов (k = 8)
3. построить гистограмму распределения;
4.найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 3.
Пусть дана последовательность значений некоторого признака: 15,4; 15,5; 16,2; 15,9; 13,6; 15,6; 13,7; 16; 16,2; 16,0; 14,2; 16,1; 15,8; 15,2; 16,2; 15,3; 14,5; 15,0; 15,0; 16,3; 15,8; 14,2; 15,3; 15,2; 16,0; 14,2; 14,5; 14,2; 15,6; 15,0; 16,8, 16,8. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 4);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5 найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 4.
Пусть дана последовательность значений некоторого признака: 14; 14; 25; 15; 12; 8; 18; 23; 14; 11; 18; 18; 12; 29; 16; 17; 13; 15; 20; 10; 17; 16; 18; 16; 14; 9; 15; 13; 20; 28; 9; 20. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 7);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 5.
Пусть дана последовательность значений некоторого признака: 35; 39; 24; 30; 47; 28; 31; 41; 36; 38; 40; 25; 31; 36; 38; 36; 27; 29; 30; 31; 35; 31; 35; 41; 36; 51; 36; 38; 33; 29; 32. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на kинтервалов (k = 9);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 6.
Пусть дана последовательность значений некоторого признака:182; 184; 176; 177; 180; 184; 186; 186; 179; 190; 170; 172; 185; 184; 182; 180; 177; 176;172; 189; 174; 176; 172; 174; 175; 182; 186; 186; 183; 165; 177; 172. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 5);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 7.
Пусть дана последовательность значений некоторого признака: 64; 60; 66; 62; 64; 68; 70; 66; 70; 68; 62; 68; 70; 72; 60; 76; 70; 74; 62; 70; 72; 72; 64; 70; 72; 66; 76; 68; 70; 58; 76; 74; 76; 82; 76; 72; 76; 74; 79; 78; 74; 78; 74; 74; 74; 78; 76; 78; 76; 80; 80; 80; 78; 78; 81. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 6);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 8.
Пусть дана последовательность значений некоторого признака: 24; 11; 12; 13; 24; 23; 23; 24; 21; 22; 21; 23; 22; 21; 14; 14; 22; 20; 20; 20; 15; 15; 16; 20; 20; 16; 16; 20; 17; 17; 19; 19; 19; 18; 18; 18; 18; 19; 19; 18; 18; 17; 17; 19; 26. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 5);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 9.
Пусть дана последовательность значений некоторого признака: 12; 14; 13; 15; 16; 16; 16; 19; 19; 20; 20; 20; 19; 13; 15; 12; 15; 13; 14; 12; 17; 12; 17; 16; 17; 13; 16; 17; 18; 14; 15; 16; 18; 14; 15; 14; 17; 18; 14; 18; 20; 17; 18; 19; 20; 21; 22. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 5);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Вариант 10.
Пусть дана последовательность значений некоторого признака: 3; 8; 14; 14; 7; 6; 4; 12; 13; 3; 4; 5; 10; 11; 15; 10; 10; 11; 12; 8; 9; 7; 7; 8; 9; 9; 7; 8; 12; 6; 10; 9. Выполните статистическую обработку данных по следующей схеме:
1. выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2. составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов (k = 4);
3. построить гистограмму распределения;
4. найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5. найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Задание 2.
Вариант 1.
Вычислить выборочный коэффициент корреляции по следующим данным:
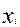
| |||||||||
 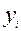
|
Проверить его значимость с надежностью 0,95.
Вариант 2.
Вычислить выборочный коэффициент корреляции по следующим данным:
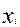
| ||||||||
 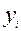
|
Проверить его значимость с надежностью 0,95.
Вариант 3.
Вычислить выборочный коэффициент корреляции по следующим данным:
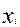
| |||||||||||
 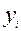
|
Проверить его значимость с надежностью 0,95.
Вариант 4.
Вычислить выборочный коэффициент корреляции по следующим данным:
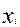
| |||||||||||||
 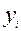
|
Проверить его значимость с надежностью 0,95.
Вариант 5.
Вычислить выборочный коэффициент корреляции по следующим данным:
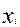
| |||||||
 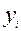
|
Проверить его значимость с надежностью 0,95.
Вариант 6.
Вычислить выборочный коэффициент корреляции по следующим данным:
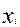
| |||||||
 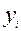
|
Проверить его значимость с надежностью 0,95.
Вариант 7.
Вычислить выборочный коэффициент корреляции по следующим данным:
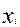
| ||||||
 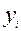
|
Проверить его значимость с надежностью 0,95.
Вариант 8.
Вычислить выборочный коэффициент корреляции по следующим данным:
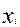
| |||||||||||
 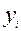
|
Проверить его значимость с надежностью 0,95.
Вариант 9.
Вычислить выборочный коэффициент корреляции по следующим данным:
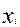
| |||||||||||||
 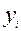
|
Проверить его значимость с надежностью 0,95.
Вариант 10.
Вычислить выборочный коэффициент корреляции по следующим данным:
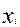
| |||||||||||
 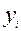
| 0,3 | 2,75 | 3,5 |
Проверить его значимость с надежностью 0,95.
Задание 3.
Вариант 1.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 2.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 3.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 4.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 5.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 6.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 7.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 8.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 9.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Вариант 10.
Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
| № испытуемых п/п | Время решения первого задания теста (в сек.). | Время решения второго задания теста (в сек.). | Время решения третьего задания теста (в сек.). |
Решение типовых заданий
Задание 1. Пусть дана последовательность значений некоторого признака: 20, 21, 22, 23, 25, 25, 26, 27, 27, 25, 26, 27, 25, 22, 23, 24, 39, 23, 40, 22, 26, 30, 24, 24, 25, 24, 25, 24, 28, 24, 29, 25, 26, 27, 30, 31, 34, 31, 35, 32, 30, 30, 25, 35, 38, 39, 28, 34, 35, 36. Выполните статистическую обработку данных по следующей схеме:
1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения при n = 50;
2) составить равноинтервальный вариационный ряд, разбив всю вариацию на kинтервалов (k=5);
3) построить гистограмму относительных частот распределения;
4) найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5) найти доверительный интервал для генеральной средней  г. Принять уровень значимости α = 0,05.
г. Принять уровень значимости α = 0,05.
Справочный материал
Основные понятия и формулы для математической обработки информации по каждому пункту задания.
· Расположение выборочных наблюдаемых значений случайной величины в порядке неубывания называется ранжированием.
· Дискретным (безинтервальным) вариационным рядом распределения называется ранжированная совокупность вариант 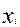 с соответствующими им частотами или относительными частотами.
с соответствующими им частотами или относительными частотами.
· Равноинтервальным вариационным рядом (интервальным распределением частот) называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений случайной величины.
· Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой, а изменение этого значения – варьированием.
· Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой или весом варианты. Если i – индекс варианты, то mi – число измеренных значений i-й варианты.
· Отношение mi к общей сумме частот всех вариант Ʃmi = n называется относительной частотой варианты и обозначается 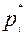 = mi / n .
= mi / n .
· Мода – называется варианта, которая имеет наибольшую частоту (Мо).
· Медиана – называется варианта, которая делит вариационный ряд на две части, равные по числу вариант (me).
Числовые характеристики выборочной совокупности: выборочная средняя  в, выборочная дисперсия Dв, и выборочное среднее квадратическое отклонение σв.
в, выборочная дисперсия Dв, и выборочное среднее квадратическое отклонение σв.
Формулы для нахождения числовых характеристик выборочной совокупности:
 в =
в = 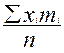 - выборочная средняя
- выборочная средняя
Dв = 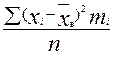 - выборочная дисперсия
- выборочная дисперсия
σв = 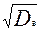 - выборочное среднее квадратическое отклонение
- выборочное среднее квадратическое отклонение
S2 = 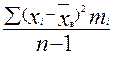 - исправленная дисперсия
- исправленная дисперсия
δ = tα,n 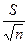 , где tα,n – коэффициент Стьюдента, зависящий от объема выборки и доверительной вероятности, значение которого берется из справочной таблицы приложений учебной литературы, δ – заданная точность, с какой намечено получить средний результат.
, где tα,n – коэффициент Стьюдента, зависящий от объема выборки и доверительной вероятности, значение которого берется из справочной таблицы приложений учебной литературы, δ – заданная точность, с какой намечено получить средний результат.
Если количественный признак Х генеральной совокупности распределен нормально, то доверительный интервал для оценки математического ожидания случайной величины Х (истинного значения измеряемой величины) рассчитывается по формуле:
( в – δ,
в – δ,  в + δ) – доверительный интервал для среднего значения.
в + δ) – доверительный интервал для среднего значения.
Решение:
1) Выполним ранжирование признака
20, 21, 22, 22, 22, 23, 23, 23, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 26, 26, 26, 26, 27, 27, 27, 27, 28, 29, 30, 30, 30, 30, 31, 31, 32, 34, 34, 35, 35, 35, 36, 38, 38, 39, 39, 40
Составим безинтервальный вариационный ряд распределения при n = 50
| i | |||||||||||||||||||
| xi | |||||||||||||||||||
| mi |
2) Составим равноинтервальный вариационный ряд, разбив всю вариацию на kинтервалов (k=5)
Определим в данной выборке хmax = 40; xmin = 20 .
Рассчитаем ширину частичного интервала h = 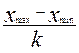 =
= 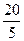 = 4, где
= 4, где
k – число равных интервалов. Определим частоту вариант, попавших в соответствующий частичный интервал и относительную частоту.
| № интервала | Частичный интервал | Частота вариант mi | Относительная
частота 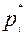
|
| 20-24 | 14/50 = 0,28 | ||
| 24-28 | 17/50 = 0,34 | ||
| 28-32 | 8/50 = 0,16 | ||
| 32-36 | 6/50 = 0,12 | ||
| 36-40 | 5/50 = 0,1 |
3) Построим гистограмму относительных частот распределения, отложив по оси абсцисс (xi) интервалы, по оси ординат ( 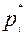 ) относительные частоты (смотри рис.1.).
) относительные частоты (смотри рис.1.).
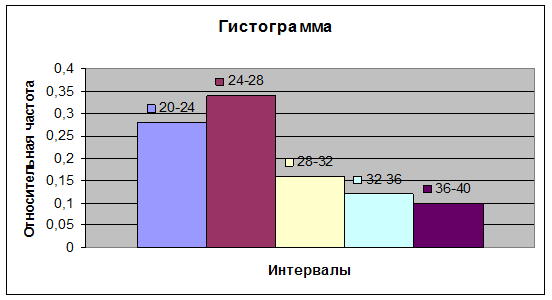
Рис.1. Гистограмма относительных частот распределения
4) Рассчитаем числовые характеристики выборочной совокупности
 в =
в = 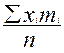 =
= 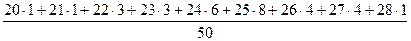 +
+
+ 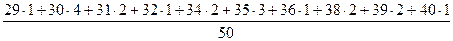 = 28,12
= 28,12
Dв = 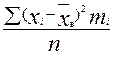 =
= 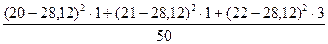 +
+
+ 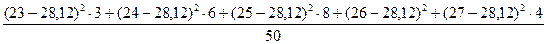 +
+
+ 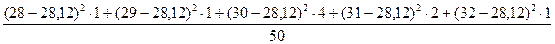 +
+
+ 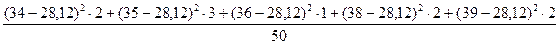 +
+
+ 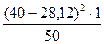 =
= 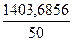 = 28,0737
= 28,0737
σв = 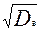 =
= 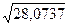 = 5,3
= 5,3
Мода равна - 25.
Медиана равна – 29.
5) Рассчитаем границы доверительного интервала для среднего значения (математического ожидания μ)  в, принимая уровень значимости α = 0,05.
в, принимая уровень значимости α = 0,05.
Вычислим исправленную дисперсию по формуле
S2 = 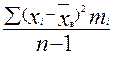 =
= 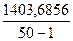 =
= 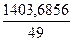 = 28,6466
= 28,6466
Найдем исправленное среднее квадратическое отклонение
S = 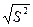 =
= 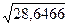 = 5,35
= 5,35
По таблице приложения (основной литературы) определим значение коэффициента Стьюдента tα,n= 2,009 при α = 0,05 n = 50
Определим точность оценки по формуле δ = tα,n 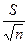
δ = 2,009 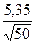 = 0,28
= 0,28
( в – δ< μ<
в – δ< μ<  в + δ)
в + δ)
(28,12 - 0,28 < μ < 28,12 + 0,28) или (27,84; 28,40)
Ответ:  в = 28,12; М0 = 25; me = 29; Dв = 28,0737; σв = 5,3; (27,84; 28,40) – доверительный интервал для генеральной средней
в = 28,12; М0 = 25; me = 29; Dв = 28,0737; σв = 5,3; (27,84; 28,40) – доверительный интервал для генеральной средней  г.
г.
Задание 2. Вычислить выборочный коэффициент корреляции по следующим данным:
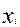
| |||||
 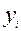
|
Проверить его значимость с надежностью 0,95.
Справочный материал
На практике для оценки коэффициента корреляции между величинами Х и У по результатам выборочных данных проведенного исследования используется выборочный коэффициент корреляции, определяемый по формуле:
rв = 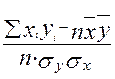 , где n – число измерений (число пар хiyi),
, где n – число измерений (число пар хiyi),
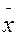 и
и 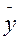 - средние выборочные для совокупностей вариант хi и yi, σх и σу – средние квадратические отклонения для указанных совокупностей.
- средние выборочные для совокупностей вариант хi и yi, σх и σу – средние квадратические отклонения для указанных совокупностей.
Решение:
Рассчитаем величины, входящие в формулу выборочного коэффициента корреляции
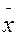 =
= 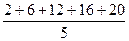 = 11,2
= 11,2 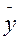 =
= 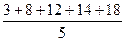 = 11
= 11
Ʃхiyi = 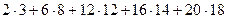 = 782
= 782
σх = 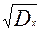 =
= 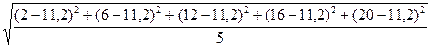 =
= 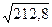 =
=
= 14,59
σу = 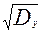 =
= 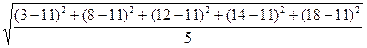 =
= 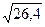 = 5,14
= 5,14
Подставим вычисленные величины в формулу для выборочного коэффициента корреляции
rв = 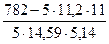 = 0,44
= 0,44
Чтобы проверить его значимость с надежностью 0,95, надо обратиться к справочному материалу.
Справочный материал
Пусть двумерная генеральная совокупность (Х,У) распределена нормально. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции rв, который оказался отличным от нуля. Если нулевая гипотеза отвергается, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля, а Х и У коррелированны, т.е. связаны линейной корреляционной зависимостью. Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, а Х и У некоррели
|
из
5.00
|
Обсуждение в статье: Решение типовых заданий |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

