 |
Главная |
Тема: Исследование функции на непрерывность
|
из
5.00
|
Для исследования функции на непрерывность необходимо:
1. Найти область определения функции;
2. Рассмотреть односторонние пределы в точках, где функция не существует; если функция кусочная, то рассмотреть односторонние пределы в точках «склейки»;
3. Исследовать функцию на бесконечности;
4. Построить эскиз графика функции.
Для классификации точек разрыва функции 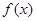 можно пользоваться таблицей, приведенной ниже.
можно пользоваться таблицей, приведенной ниже.
Пусть 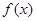 – заданная функция,
– заданная функция,  – исследуемая точка,
– исследуемая точка,  – соответственно левый и правый пределы функции.
– соответственно левый и правый пределы функции.
| Тип разрыва | Условия |
| Функция непрерывна | 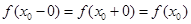
|
| Устранимый разрыв | 
|
| Разрыв первого рода (скачок) | 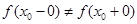
 – конечны – конечны
|
| Разрыв второго рода | 
|
Рассмотрим примеры.
Пример 1. Задана функция  .
.
Областью определения функции является множество  . Действительно, функция не существует в единственной точке
. Действительно, функция не существует в единственной точке  , следовательно, эта точка и будет точкой разрыва. Именно в ней мы должны найти односторонние пределы (левосторонний и правосторонний).
, следовательно, эта точка и будет точкой разрыва. Именно в ней мы должны найти односторонние пределы (левосторонний и правосторонний).
· Если отыскивается предел функции  в точке
в точке  при условии, что
при условии, что  и
и  , то этот предел, если он существует, называется левосторонним пределом функции и обозначается
, то этот предел, если он существует, называется левосторонним пределом функции и обозначается 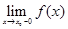 .
.
· Если отыскивается предел функции  в точке
в точке  при условии, что
при условии, что  и
и  , то этот предел, если он существует, называется правосторонним пределом функции и обозначается
, то этот предел, если он существует, называется правосторонним пределом функции и обозначается 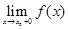 .
.
Найдем односторонние пределы в точке  .
.


· Если левосторонний предел и правосторонний предел функции в точке  существуют, но не равны между собой, то есть
существуют, но не равны между собой, то есть 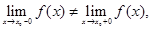 то точка
то точка  называется точкой разрыва первого рода.
называется точкой разрыва первого рода.
Согласно теории, точка  является точкой разрыва первого рода, то есть в ней функция претерпевает скачок.
является точкой разрыва первого рода, то есть в ней функция претерпевает скачок.
Далее исследуем поведение функции на бесконечности, для этого найдем пределы при 
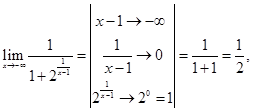

Следовательно, 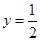 – прямая, которая является для функции горизонтальной асимптотой.
– прямая, которая является для функции горизонтальной асимптотой.
Сделаем эскиз графика.


Пример 2. Задана функция  .
.
Областью определения функции является множество  . Действительно, функция не существует в единственной точке
. Действительно, функция не существует в единственной точке 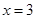 , следовательно, эта точка и будет точкой разрыва. Определим с помощью односторонних пределов тип разрыва в этой точке.
, следовательно, эта точка и будет точкой разрыва. Определим с помощью односторонних пределов тип разрыва в этой точке.

·  - это неопределенность, которую можно раскрыть, разложив на множители числитель и знаменатель.
- это неопределенность, которую можно раскрыть, разложив на множители числитель и знаменатель.

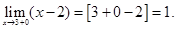
· Если в точке  функция
функция  имеет левосторонний и правосторонний пределы, и эти пределы равны между собой, но их значения не совпадают со значением функции в этой точке, то эта точка называется точкой устранимого разрыва:
имеет левосторонний и правосторонний пределы, и эти пределы равны между собой, но их значения не совпадают со значением функции в этой точке, то эта точка называется точкой устранимого разрыва: 
Делаем вывод, что точка 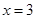 будет точкой устранимого разрыва.
будет точкой устранимого разрыва.
Графиком функции является прямая с выколотой точкой при 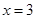 .
.
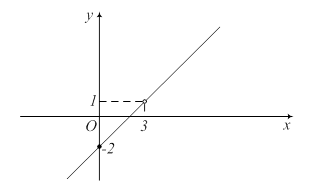
Построим график функции, для этого подберем кроме точки (3,1) еще одну произвольную. Пусть это будет (0,–2).
Сделаем эскиз графика функции.
Устранимый разрыв можно ликвидировать, если доопределить функцию в точке разрыва, задав:
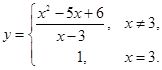
Пример 3. Функция 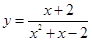 имеет две точки разрыва:
имеет две точки разрыва: 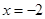 и
и  . Найдем односторонние пределы в этих точках.
. Найдем односторонние пределы в этих точках.
Рассмотрим  Разложив знаменатель на множители и сократив, получим следующее:
Разложив знаменатель на множители и сократив, получим следующее:  – это гипербола, с точками разрыва
– это гипербола, с точками разрыва 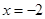 и
и  .
.
Тогда 
Делаем вывод, что точка 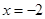 является точкой устранимого разрыва.
является точкой устранимого разрыва.
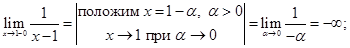


· Если в точке  не существует левосторонний или правосторонний предел функции (или оба одновременно), то эта точка называется точкой разрыва второго рода (бесконечный разрыв).
не существует левосторонний или правосторонний предел функции (или оба одновременно), то эта точка называется точкой разрыва второго рода (бесконечный разрыв).
Найдем предел функции на бесконечности:
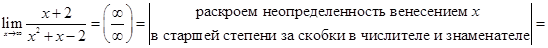
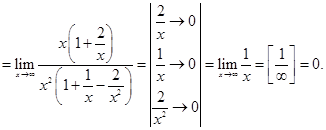
Следовательно, прямая y= 0 будет горизонтальной асимптотой для заданной функции.
Построим график функции:

Рассмотрим примеры кусочных функций.
Пример 4. 
Функции  являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в
являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в 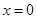 ,
,  . Исследуем поведение функции в окрестности этих точек:
. Исследуем поведение функции в окрестности этих точек:

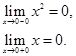
При 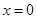 функция
функция  определена и равна нулю, а функция
определена и равна нулю, а функция  в эту точку не заходит по условию.
в эту точку не заходит по условию.
· Функция  называется непрерывной в
называется непрерывной в  , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть
, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть 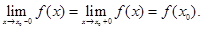
Следовательно, точка x= 0 является точкой непрерывности функции.

Делаем вывод, что точка x= 2 является точкой разрыва первого рода и непрерывна слева (по условию).
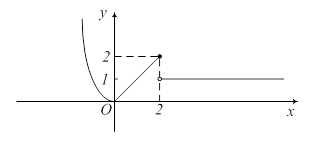
Строим график склеенной функции:
Пример 5. 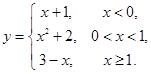
Элементарные непрерывные функции  и
и  не определены в точке
не определены в точке 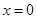 , а функции
, а функции  и
и  «склеены» в точке
«склеены» в точке  , которая, быть может, также является точкой разрыва. Исследуем поведение функции в этих точках.
, которая, быть может, также является точкой разрыва. Исследуем поведение функции в этих точках.


Точка 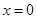 является точкой устранимого разрыва.
является точкой устранимого разрыва.
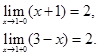
При  функция
функция  принимает значение, равное 2. Следовательно, точка
принимает значение, равное 2. Следовательно, точка  является точкой непрерывности.
является точкой непрерывности.
Строим график заданной функции:
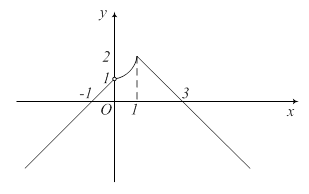
Пример 6. 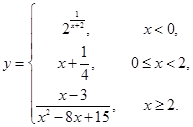
Функция задана несколькими аналитическими выражениями, поэтому точки разрыва могут быть как в точках склейки 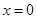 ,
,  , так и в точках
, так и в точках 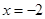 ,
, 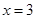 ,
,  , где знаменатели дробей обращаются в нуль.
, где знаменатели дробей обращаются в нуль.
Сделаем некоторые упрощения: 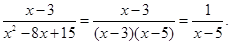 Далее будем рассматривать функцию
Далее будем рассматривать функцию 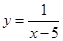 с точками разрыва
с точками разрыва 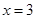 ,
,  .
.

Исследуем все точки:
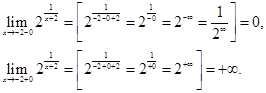
Точка 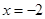 – точка разрыва второго рода.
– точка разрыва второго рода.

Точка 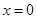 – точка разрыва первого рода, функция непрерывна справа (по условию).
– точка разрыва первого рода, функция непрерывна справа (по условию).

Точка  – точка разрыва первого рода, функция непрерывна справа (по условию).
– точка разрыва первого рода, функция непрерывна справа (по условию).
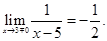
Точка 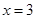 является точкой устранимого разрыва.
является точкой устранимого разрыва.
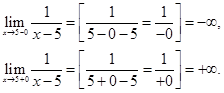
Точка  является точкой разрыва второго рода.
является точкой разрыва второго рода.
Исследуем поведение функции  при
при 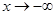 , а функции
, а функции 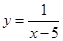 при
при 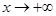 .
.

Сделаем эскиз графика функции:

|
из
5.00
|
Обсуждение в статье: Тема: Исследование функции на непрерывность |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

