ст. преп. Денищик С.С

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра АУТП

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ В SIMULINK

По курсу “Компьютерная графика”

Выполнил: ст. гр. АКГ-09

Курбанов Г.Р.

Проверил: ст.преп. Склярова Г.А

асс. Марусей О.В

ст. преп. Денищик С.С.

 

Алчевск 2011

СОДЕРЖАНИЕ

 

Введение.......................................................................................................... ……4

1 Моделирование входных сигналов (моделирование объекта X).............. ……6

1.1 Общие принципы представления сигналов математическими моделями ……6

1.2 Моделирование сигнала заданного вида................................................. ……7

2 Моделирование объекта A........................................................................ ……12

3 Моделирование объекта B........................................................................ ……14

4 Моделирование системы........................................................................... ……16

5 Анализ результатов моделирования......................................................... ……19

Выводы.......................................................................................................... ……20

Перечень ссылок............................................................................................ ……21

 

ВВЕДЕНИЕ

 

Моделирование различных систем, объектов, процессов, явлений природы и т.д. имеет важное значение в науке и технике. Благодаря моделированию существенно облегчается и удешевляется исследование физических, химических и других природных явлений, технических объектов, создание образцов новой техники. Моделированием называется создание моделей реальных объектов и их экспериментальные исследования. В свою очередь модель – это, как правило, упрощенное отражение реального объекта, несущее те его качества, которые подвергаются исследованию (моделированию).

Большое значение имеют, так же, математические модели. Они позволяют производить моделирование реальных объектов и систем с использованием многочисленных математических методов, оперируя со свойствами объектов, выраженными в виде различных математических зависимостей и соотношений. Математические модели той или иной степени сложности, как правило, идеализированы и отражают только исследуемые характеристики реальных объектов.

С математическими моделями тесно связаны компьютерные модели, которые в зависимости от программы в которой производится моделирование, используют те или иные математические характеристики реальных объектов. В настоящее время в связи со значительным прогрессом в области компьютерной техники компьютерное моделирование приобрело большое значение в науке и технике. На сегодняшний день существует значительное количество специализированных пакетов, таких как MatLab, MathCad, Math, Mathematica, Maple и др., которые дают широкие возможности для компьютерного моделирования различных процессов и систем.

Целью данной курсовой работы является изучение принципов решения различных технических задач с использованием компьютерной техники и приобретение практических навыков моделирования процессов и объектов.

В результате выполнения курсовой работы необходимо изучить принципы построения моделей в программе Simulink, освоить методику моделирования в ней и расширить знания и навыки при решении математических задач (к которым сводится большинство практических задач науки и техники) в пакете MatLab в целом. Необходимо, также, научиться строить графические зависимости различных функций, работать с табличными данными, конвертировать таблицы и графики в текстовый редактор Word и оформлять текстовые документы, включающие в себя формулы, таблицы, графические объекты.

 

 

1 МОДЕЛИРОВАНИЕ ВХОДНОГО СИГНАЛА

1.1 Общие принципы представления сигналов математическими моделями

 

 

Входной сигнал может задаваться различными математическими моделями: динамическим представлением, геометрическим, спектральным, энергетическим. Динамическое представление произвольного сигнала с использованием функции Хевисайда:

(1.1)

 

При геометрическом представлении вводится понятие координатного базиса: если совокупность векторов (e1, e2, еЗ, ...) является линейно независимой, то она образует координатный базис в линейном пространстве. Тогда сигнал s(t) можно представить в виде

(1.2)

 

где числа (c1, c2, сЗ, ...) являются проекциями сигнала s(t) относительно выбранного базиса.

При спектральном представлении сигнал s(t) и его спектральная плотность S(ω) взаимно-однозначно связаны прямым и обратным преобразованиями Фурье:

(1.3)

 

(1.4)

 

1.2 Моделирование сигнала заданного вида

 

 

Необходимо промоделировать сигнал, представляющий собой произведение двух функций X₈*X₂₀

Сигнал Х₈ задан функцией вида:

 

, (1.5)

 

где A = 80 , Т = 8ms φ = 0⁰

 

Сигнал Х₂₀ задан функцией вида:

 

, (1.6)

 

A = 67, T = 20ms, φ = 180⁰

После преобразований составим структурную схему в Simulink для моделирования заданных сигналов, а так же для моделирования результирующего сигнала(см.рисунок 1.1,1.3,1.5 соответственно)

 

Произведено моделирование структуры. Получены временные и выходные характеристики приведены на рисунках 1.2,1.4,1.6.они представляют собой согласно варианту задания

 

 

Рисунок 1.1– Структурная схема для моделирования сигнала X₁₅

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 1.3– Структурная схема для моделирования сигнала X₃

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 1.5– Структурная схема для моделирования комбинированного сигнала

 

 

 

 

 

 

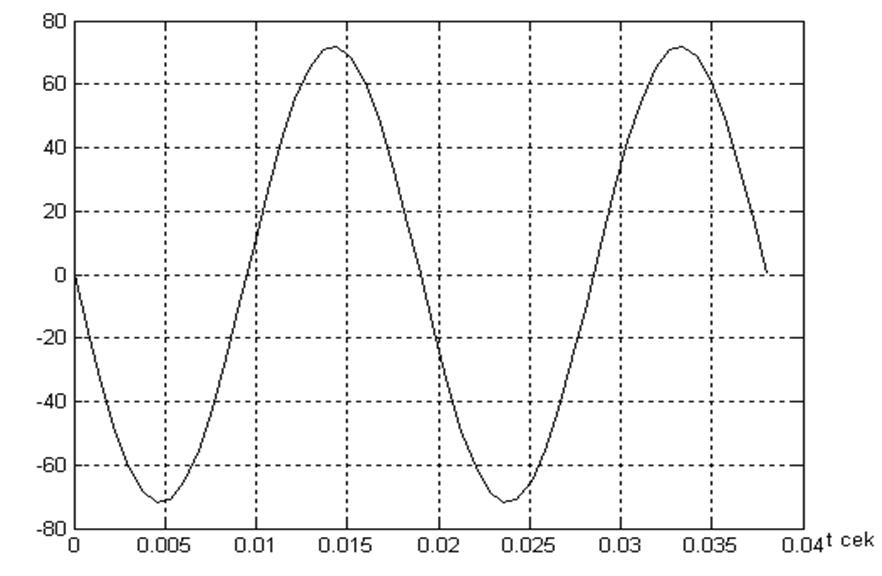
Рисунок 1.2 – График сигнала модели X

 

 

 

 

 

 

Рисунок 1.4 – График сигнала модели X

 

 

 

Рисунок 1.6 - График результирующего сигнала (X₁₅+X₃)

2 МОДЕЛИРОВАНИЕ ОБЪЕКТА A

 

Объект A задан дифференциальным уравнение четвертого порядка:

. (2.1)

 

Анализируя данное уравнение перейдем к выводу, что оно решается операторным методом????????,так как в правой части уравнения есть производная от входного воздействия х.

Окончательный вид уравнения(2.1)получим,перенеся высшую производную в левую часть и разделив обе части уравнения на коэффициент при старшей производной:

 

(2.2)

 

Полученное уравнение называется машинным и позволяет осуществить построение структурной схемы для моделирования объекта приведенную на рисунке 2.1. Схема имеет 4 интегратора, количество которых соответствует порядку производной .В результате моделирования структуры получен график временной выходной функции этой структуры ,приведенный на рисунке 2.2

Как видно из графика решения дифференциального уравнения представленного на рисунке 2.2 он имеет расходящийся характер

 

 

 

Рисунок 2.1 - Структурная схема для решения дифференциального уравнения общин методом

 

 

 

Рисунок 2.2- График решения дифференциального уравнения во временной области

 

 

3 МОДЕЛИРОВАНИЕ ОБЪЕКТА В

 

Объект В,согласно индивидуального задания , задан произведением двух передаточных функций типовых динамических звеньев первого порядка вида:

 

W(p)= W8*W4 (3.1)

где, в свою очередь, передаточные функции W5(p) и W8(p) представлены ниже в общем виде :

 

 

(3.2)

 

Для формирования структурной схемы объекта, представляющего собой типовое соединение звеньев, запишем параметры их передаточных функций – коэффициенты усиления и постоянные времени :

 

K = ; T₁= с; T₂= с; T₃= с.

С помощью блоков Transfer Fcn пакета визуального моделирования Simulink была разработана структурная схема объекта В, представленная на рисунке 3.1. Для исследования объекта В, заданного произведением передаточных функций, в качестве входного воздействия выбрана типовая функция Хевисайда (функция включения).

При моделировании объекта В и входящих в его состав передаточных функций были получены графики переходных характеристик отдельных передаточных функций (см. рисунки 3.2 и 3.3 соответственно), и график переходной функции объекта В, представленный на рисунке 3.4.

 

 

 

 

 

 

 

Рисунок 3.1– Структурная схема модели объекта B

 

 

Рисунок 3.1– Структурная схема модели объекта B

 

 

Рисунок 3.2 – Переходная характеристика звена W8(p)

 

 

 

Рисунок 3.3 – Переходная характеристика звена W4(p)

 

 

 

Рисунок 3.4 – Переходная характеристика объекта В

 

 

4 МОДЕЛИРОВАНИЕ СИСТЕМЫ

 

Общая структуры системы, согласно варианта задания, представляет собой параллельное соединение объектов А и В, согласно рисунка 4.1.

 

Рисунок 4.1 – Структурная схема модели системы при параллельном

подключении объектов

 

Она представлена паследовательным соединением объекта А, заданного дифференциальным уравнением 3-ого порядка и объекта В, заданного суммой передаточных функций W8(p) и W4(p).

В качестве внешнего сигнала, подаваемого последовательно на объект А и объект В, выбрана типовая функция Хевисайда (функция включения). Структурная схема синтезированной системы представлена на рисунке 4.2.

Осуществлено моделирование синтезированной системы. В результате получен график выходной функции, представляющей собой реакцию динамической системы на типовое внешнее воздействие – переходную характеристику. Ее вид представлен на рисунке 4.3. Как видно из рисунка 4.3, временная характеристика синтезированной системы носит расходящийся характер.

 

 

 

Рисунок 4.2 – Структурная схема синтезированной системы

 

 

Рисунок 4.3 – Переходная характеристика синтезированной системы

5 АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ

 

В процессе моделирования заданных сигналов X₈ и X₂₀ разработана структурная схема (рисунок 1.1 ) и получены функции представленные на рисунках 1.2. 1.4. 1.6. . Сигнал X₁₅ и Х₃ представляет собой экспоненциальную функцию, что можно наблюдать на рисунке 1.2 1.4. Также был разработан комбинированный сигнал Х, который представлен структурной схемой (см. рисунок 1.5) и временной выходной функцией (см. рисунок 1.6).

Объект А задан дифференциальным уравнением (2.1) и имеет третий порядок. Для оценки параметров объекта А строится переходная характеристика, которая является откликом исследуемой системы на функцию включения (функцию Хевисайда). График переходной характеристики приведен на рисунке 2.2. Она имеет расходящийся характер.

Объект В задан передаточными функциями (3.2) первого порядка. Для оценки параметров объекта В строится переходная характеристика, которая является откликом исследуемой системы на функцию включения (функцию Хевисайда). График переходной характеристики приведен на рисунке 3.4.

Паралельным соединением объектов А и В была синтезирована динамическая система, представленная структурной схемой на рисунке 4.2. Переходный процесс полученный при прохождении единичного скачкообразного воздействия через исследуемую систему, представлен на рисунке 4.3 и носит расходящийся характер.

 

 

ВЫВОДЫ

 

В результате выполнения курсовой работы были получены следующие результаты.

Смоделированы сигналы Х₁₅, Х₃ а так же Х₁₅ + Х₃ графики которых приведены на рисунках 1.2, 1.3 и 1.4 соответственно.

Построена структурная схема объекта A заданного дифференциальным уравнением (рис. 2.1). Произведено ее моделирование и получена переходная характеристика (рис. 2.2).

Объект Б был задан передаточной функцией (3.1). Переходная характеристика объекта Б показана на рис. 3.1.

Была смоделирована общая структурная схема (рис. 4.1) и получены выходные характеристики показанные на рисунке 4.2 и 4.3.

В процессе работы над курсовым проектом были приобретены навыки моделирования сигналов и систем . Были закреплены знания и навыки, полученные в курсах КГ, КТ и ОВР.

Проделанная работа была осуществлена с помощью грамотно составленных методических указаний и консультаций ведущего преподавателя.

Полученные знания и навыки будут использоваться мною в дальнейшем при изучении других дисциплин, написании курсовых проектов и дипломной работы, а также в моей будущей инженерной и научной деятельности.

 

ПЕРЕЧЕНЬ ССЫЛОК

 

1. И.В.Черных. Simulink: Инструмент моделирования динамических систем. – M.:Exponenta. 2000

2. Потемкин В.Г. Система инженерных и научных расчетов MATLAB 5.x: в 2-х томах. Том 1.-М.: ДИАЛОГ МИФИ. 1999. – 366 с.

3. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. - СПб.: КОРОНА принт, 1999. – 288 с.

4. Теория систем автоматического регулирования, издание третье, исправленное. Бесекерский В. А., Попов Е. П. М.: Наука. 1975, 768с.

5. Воронов А.А. Основы теории автоматического регулирования. Часть 1. М–Л.: Энергия. 1965. 396с.

6. Луценко В.А.. Финякин Л.Н. Математическое моделирование химико– технологических процессов на АВМ. – М.: Химия. 1978.

7. Горбацевич Е.Д. Левинзон Ф.Ф. Аналоговое моделирование систем управления. – М.: Наука. Главная редакция физико – математической литературы. 1984. – 304с.

8. Левин В.И., Гросберг Ю.И. Дифференциальные уравнения математической физики. – М.: Гостехиздат. 1951.

9. Гельман В.Я. Практикум по математике на компьютере. СПб.: СПИГ. 2001.

10. Мякинный О.A. Mikrosoft Word 2003: Самоучитель / О.А. Мякинный. - М.: Диалектика. 2004. - 272 с.