 |
Главная |
Представл деревьев в ЭВМ
|
из
5.00
|
Дерево –связный граф без циклов. Всякое дерево м ориентировать, назначив один из узлов корнем, и произвольно упорядочить. Всякое упорядоч дерево м представить бинарн деревом, проведя правую связь к брату, а левую к сыну.
<Придумать пример>
Представление бинарных деревьев в ЭВМ
Прямая запись в скобках: (A(B(D))(C(E)(F)))
Списочные струк-ры: ∀ узел представлен записью, содерж 2 поля с указателями на лев. и прав. узлы и поле на хране-ние инф. об узле. O(p)=3n. Упаковочные массивы: элем записыв-ся последовательно, т.ч. все узлы поддерева данного узла располаг-ся вслед за этим узлом. также фиксир-ся «размеченная степень» ∀ узла: 0 - лист, 1 – есть лев. связь, но нет правой, 2 – есть правая связь но нет лев., 3 – обе свзязи. O(p)=2p
Обходы графов
Обход графа- просмотр всех его вершин в некот. порядке.
Обход в глубину- метод обх гр, в кот. всегда происходит продвижение от текущ верш к смежной с ней,
6. Методы решения комбинаторных оптимиз-х задач
Метод ветвей и границ –общ. алгоритмический метод для нахождения оптим-х решен различн зад оптимиз-и.
По сути метод явл-ся вариацией полного перебора с отсевом подмн-в допуст-х реш-й, заведомо не содер-х оптим-х реш-й.
Пусть з-ча P, G-мн-во допуст реш. Сразу P решить оптима-льно не можем. =>делим P на подзад P1,…Pk, у кот. есть G1,…Gk. Структуры з-ч P и Pi одинак =>  Сразу Pi тоже решить не можем => приводим к др.виду – ослабление з-чи: PR1,…PRk – их решить можем, для кот ∃ GR1,…GRk, где
Сразу Pi тоже решить не можем => приводим к др.виду – ослабление з-чи: PR1,…PRk – их решить можем, для кот ∃ GR1,…GRk, где 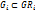 Если нет допуст.реш для PRi =>з-чу Pi м. не рассматривать.
Если нет допуст.реш для PRi =>з-чу Pi м. не рассматривать.
Рассм-м з-чу на мин-м функция F(x) , G-мн-во допуст-х реш-й, W - мн-во реш 
Процедура ветвления сост в разбиении обл. допуст реш-й (  ) на подобл. меньших размеров (рекурсивно приме-няем к подобл-м). Получ-е подобл. образуют дерево поиска решения, узлы кот. – подобл, листья – реш-я. Разбиение прекращ, когда у подзад не > 1 реш исх-й з-чи (рекорд). Мн-во м. б. разбито на подмн-во произвольным обр-м.
) на подобл. меньших размеров (рекурсивно приме-няем к подобл-м). Получ-е подобл. образуют дерево поиска решения, узлы кот. – подобл, листья – реш-я. Разбиение прекращ, когда у подзад не > 1 реш исх-й з-чи (рекорд). Мн-во м. б. разбито на подмн-во произвольным обр-м.
Процедура нахождения оценок заключ в поиске верхних и нижних границ для оптим-го зн-я на подобл. допуст-х решений.
Оценка – функц. Φ заданная на совок. подмн-в мн-ва W :
Φ(Wi) ≤ F(x) для 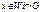
Φ(Wi) = F(x) если |Wi|=1 и 
Φ(Wi) =+ ¥ если |Wi|=1 и 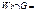 Ø
Ø
Для вычисл-я оценки реш-ся ослбл-е з-ча (PRi), оптим-е реш. кот. - оценка снизу для реш-й исх-й з-чи, содерж-ся в этой з-че.
Любое реш-е исх-й з-чи - верхняя оценка, кот. > (т.е. хуже) или = оптим-му реш-ю.
Рекорд – наилуч. из найд-х реш-й исх. з-чи (мин. из верхн оценок) (до тек. момента в реш).
Отсечение. Если для подз-чи нижняя оц получилась ⩾ рекорду, то она заведомо не содержит реш-я лучше одного из уже найд-х => дальше ее не исслед-т (идущая от нее ветвь дерева отсекается).
Выбор порядка реш-я з-чЧасто испол-ся след. способ ветвл:
- для подзадач верхнего ур получают оценки снизу;
- подз с лучшей оц разбив-ся на подз-чи след. уровня, и для них определ оценки снизу;
- эти подз-чи добавл-ся к подз-м, ветвл. кот. еще не произв-сь, из них выбир-ся для разбиен. подз-ча с лучш. нижн. оценк;
7 Методы сортировки
Сортировка - упорядочивание элементов в списке.
Сортировка мет-м пузырька:
Сравниваем k1, k2, если надо меняем местами, затем k2, k3 до kn, затем с k1, до kn-1, среднее время O(N2).
Сортировка простыми вставками: Идея метода: пусть есть массив 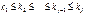 , тогда
, тогда
ключ kj последовательно сравнив с конца и ключи сдвигаются на позицию вверх, пока kj не найдет свое место. ~ O(N2).
Метод Шелла:
Идея метода: пусть есть ключи k1, …, k8, последовательность шагов h = (4, 2, 1)
1) сформируем ключи отстоящие друг от друга на 4 позиции методом простых вставок: k1, k5; k2, k6; k3, k7; k4, k8;
2) сортируем ключи отстоящие друг от друга на 2 позиции методом простых вставок: k1, k2, k3, k4; k5, k6,k7, k8
3) сортируем весь массив методом простых вставок, на каждом шаге в сортировке участвуют, либо очень короткие, либо хорошо отсортированные.
Сортировка выбором:
Пусть есть массив k1, …, kn, находим наименьший ключ и меняем местами с k1, находи наименьший ключ из k2, …, kn и меняем с k2 и т.д. O(N2).
Существует усоверш метод – пирамидальная сортировка, кот использ двоичное дерево.
Быстрая сортировка Хоара:
случ образом выбирается некотор элемент массива x, после чего массив просматр слева, пока не встретится элемент a[i] такой, что a[i] > x, а затем массив просматр справа, пока не встретится элемент a[j] такой, что a[j] < x.
8.Методы поиска
|
из
5.00
|
Обсуждение в статье: Представл деревьев в ЭВМ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

