Тема 1. НАЧАЛЬНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ

Элементы и множества

 

 

Определение.Под множеством S будем понимать любое собрание определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами множества S.

Определение.Под множеством понимают объединение в единое целое определенных вполне различаемых предметов (объектов), которые при этом называются элементами образуемого ими множества.

множества обозначают прописными буквами латинского алфавита: A, B, C, …;

а элементы множеств – строчными буквами: a, b, c, … .

 

х принадлежит М: хÎМ.

 

х не принадлежит М: хÏМ.

 

Пример 1. Это может быть множество студентов, присутствующих на лекции, множество четных чисел и т. д.

Определение. Множество А называется подмножеством множества В, если всякий элемент из А является элементом В. Если А является подмножеством В и В не является подмножеством А, то говорят, что А является строгим (собственным) подмножеством В.

 

 

.

Определение. Множество, не содержащее элементов, называется пустымÆ, оно является подмножеством любого множества. Множество U называется универсальным, то есть все рассматриваемые множества являются его подмножеством.

 

Определение. Множества А и В считаются равными, если они состоят из одних и тех же элементов, пишут А=В, А¹В – в противном случае.

Определение. Множества А и В считаются равными, если

Способы задания множеств:

§ перечислением элементов: М={a₁, a₂, …, a_k},

§ характеристическим предикатом: М={x | P(x)}

§ порождающей процедурой: M={ x | x=f},

Пример 2.

1. М={1, 2, 3, 4} –.

2. -

3. Числа Фибоначчи задаются условиями

а₁=1, а₂=2, a_n=a_n-1+a_n-2 для n>2.

Определение. Мощность конечного множества А - это число его элементов.

|A|.

Пример 3.

|Æ|=0, |{Æ}|=1.

Определение. Множества называются равномощными, если их мощности совпадают.

Определение. Множество всех подмножеств множества А называется булеаномP(A).

если множество А содержит n элементов, то множество P(A) содержит 2ⁿ элементов.

 

Пример 4.

А={0, 1, 2}, P(A)={ Æ, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}}.

 

Операции над множествами. Диаграммы Эйлера-Венна

 

 

Определение. Объединениеммножеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В

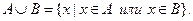
Определение. Пересечениеммножеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В

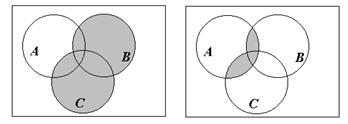
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В

 

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А

 

Пример 5. С помощью диаграмм Эйлера – Венна проиллюстрируем справедливость соотношения (рис. 6).

 

Основные тождества алгебры множеств

 

Таблица 1

1. Коммутативность объединения	1’. Коммутативность пересечения
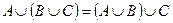
2. Ассоциативность объединения	2’. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
5. Закон де Моргана	5’. Закон де Моргана
6. Закон поглощения	6’. Закон поглощения
7. Закон склеивания	7’. Закон склеивания
10. Закон двойного дополнения

 

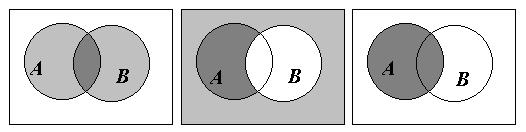
Пример 6.

Доказать следующее тождество .

Решение.

Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).

1.

2. Построим соответствующие диаграммы Эйлера-Венна (рис. 7).

Рис. 7.

Алгебраические операции

Пусть дано множество М.

Определение. Говорят, что на М определена бинарная алгебраическая операция, если всякой упорядоченной паре элементов множества М по некоторому закону ставится в соответствие вполне определенный элемент этого же множества.

 

	х1	х2	х3	х4
х1	х1	х2	х3	х4
х2	х2	х3	х1	х1
х3	х2	х3	х1	х2
х4	х4	х2	х1	х3

Таблица 2

 

Определение. Если для любых элементов a и b множества М справедливо равенство ab = ba, то операцию называют коммутативной.

Определение. Если для любых элементов a, b, c множества М справедливо равенство a(bc) = (ab)c, то операцию называют ассоциативной.