Источники и классификация погрешностей. Вычислительный алгоритм и погрешности

Вычислительный алгоритм и погрешности

Процесс исследования объекта (явления) методами математического моделирования неизбежно носит приближенный характер, так как на каждом этапе вносятся те или иные погрешности.

Так построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в данной модели ([4], стр. 8).

Их обычно обозначают 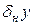, где у – точное значение величины, вычисление которой является целью поставленной задачи ([3], стр. 25). Единственный способ уменьшить эту погрешность – перейти к более точной математической модели и задать более точно исходные данные ([3], стр. 26).

При переходе от математической модели к численному методу и его реализации возникают погрешности, называемые погрешностями метода (погрешностями дискретизации) и вычислительными погрешностями (погрешностями округления) ([3], стр.26).

Дело в том, что всякий численный метод воспроизводит исходную математическую модель приближенно. Как уже было отмечено выше построение численного метода для заданной математической модели, разбивается на два этапа ([4], стр. 9):

1) формулирование дискретной задачи (построение дискретной модели);

2) разработка вычислительного алгоритма, позволяющего отыскать решение дискретной задачи.

Очевидно, что решение дискретной задачи отличается от решения исходной задачи. Разность соответствующих решений и называется погрешностью дискретизации([4], стр. 9). Обычно дискретная модель зависит от некоторого параметра (параметров) дискретизации, при стремлении которого (которых) к нулю должна стремиться и погрешность дискретизации ([4], стр. 9). Обозначим эту погрешность .

Как правило, не удается точно решить и дискретную задачу, так как приходится использовать тот или иной численный алгоритм, входные данные которого и коэффициенты, соответствующих уравнений задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления или вычислительной погрешностью ([4], стр.9). Эту погрешность обозначим .

Таким образом, полная погрешность решения задачи на компьютере , где - получаемое на компьютере решение, а у – точное значение величины, складывается из трех составляющих: неустранимой погрешности, погрешности метода и вычислительной погрешности, т.е.

.(2.1)

В литературе ([3], стр. 26) приводятся следующие рекомендации относительно выбора метода решения задачи (дискретизации) и его точности.

Желательно, чтобы погрешность метода была в 2 – 10 раз меньше неустранимой погрешности 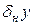. Большое значение ощутимо снижает точность результата, меньшее – обычно требует увеличение затрат на вычисления, практически уже не влияя на значение полной погрешности. Иногда характер использования результатов таков, что вполне допустимо, чтобы погрешность метода была сравнима с неустранимой погрешностью или даже несколько превышала ее.

Значение вычислительной погрешности (при фиксированных модели, входных данных и методе решения) в основном определяется характеристиками используемого компьютера. Желательно, чтобы погрешность была хотя бы на порядок меньше погрешности метода и совсем не желательна ситуация, когда она её существенно превышает.

Умение анализировать погрешности при решении прикладной задачи и соблюдать между ними разумный компромисс позволяет экономить используемы ресурсы и является признаком высокой квалификации ([3], стр. 26).