 |
Главная |
ОЦЕНКА ТРУДОЕМКОСТИ АЛГОРИТМА
|
из
5.00
|
ЛАБОРАТОРНАЯ РАБОТА № 1
Цель работы:
Освоение методов анализа трудоемкости вычислительных алгоритмов.
Задача, подлежащая решению на ЭВМ, может быть охарактеризована количеством данных, сложностью алгоритма, трудоемкостью алгоритма.
Под сложностью алгоритма понимается количество информации, необходимое для его описания. Оценка сложности алгоритма может быть дана в битах, байтах, количестве символов определенного языка. Для оценки могут использоваться также число операторов конкретного алгоритмического языка, количество машинных кодов и т.д. Предварительная оценка сложности алгоритма и количества данных выполняется экспертным путем, а точные значения могут быть известны только после завершения программирования. Сложность алгоритма и количество данных характеризуют потребность задачи в оперативной и внешней памяти.
Под трудоемкостью алгоритма понимается количество вычислительной работы, требуемой для его реализации. Трудоемкость характеризует затраты времени для реализации алгоритма на некоторой совокупности технических средств. Обычно трудоемкость оценивается количеством процессорных операций и операций ввода-вывода. Следует сразу оговориться, что трудоемкость алгоритма является в общем случае случайной величиной и зависит от исходных данных. Поэтому трудоемкость алгоритма может быть определена только приближенно в терминах теории вероятности: математическими ожиданиями, дисперсией и т.д.
Трудоемкость алгоритма в первом приближении может быть охарактеризована следующим набором параметров:
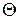 - среднее количество процессорных операций, необходимых для одной реализации алгоритма;
- среднее количество процессорных операций, необходимых для одной реализации алгоритма;
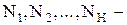 среднее количество обращений к файлам
среднее количество обращений к файлам 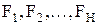 за один прогон программы через ЭВМ;
за один прогон программы через ЭВМ;
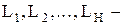 среднее количество информации, передаваемое за одно обращение к файлам
среднее количество информации, передаваемое за одно обращение к файлам 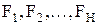 .
.
При необходимости набор параметров, характеризующих трудоемкость алгоритма может быть расширен.
Исходная информация для расчета трудоемкости алгоритма может быть взята из схемы алгоритма, используемого обычно для разработки программы. Пример такой схемы алгоритма приведен на рис. 1. Для расчета
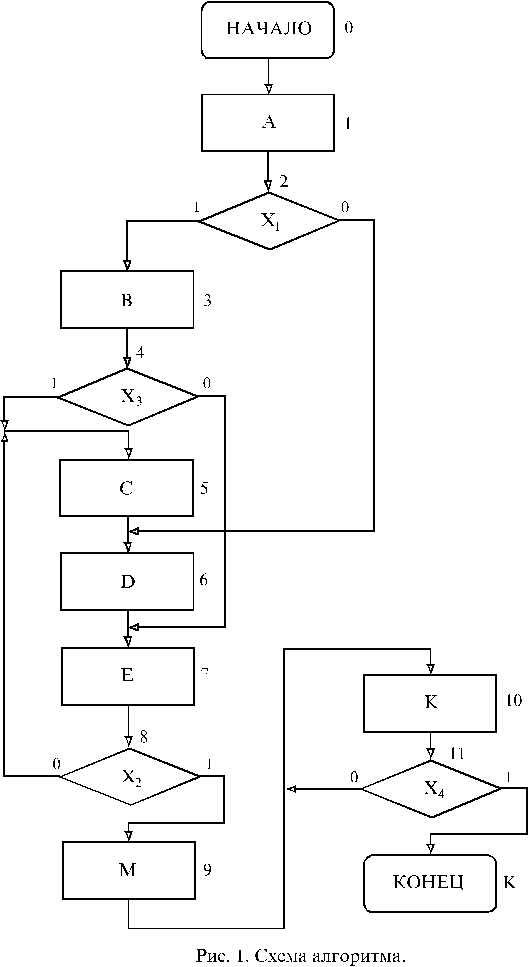
трудоемкости алгоритма необходимо дополнительно знать вероятности переходов из логических вершин при единичном значении логического условия. Если соответствующую вероятность обозначить через p, то вероятность выхода из логической вершины при нулевом логическом значении проверяемого условия будет равна 1 - p.
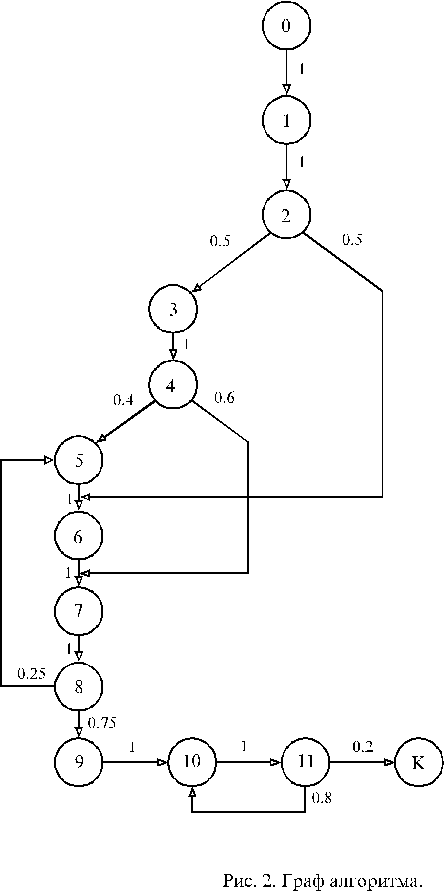
Для дальнейших расчетов схему алгоритма рациональнее изображать в виде графа алгоритма. Для этого перенумеруем все операторы схемы алгоритма. У логических операторов вместо логических условий “1” и “0” будем записывать соответствующую данному выходу вероятность. Вероят-ность выхода из операторной вершины равна 1. Полученный таким образом граф алгоритма изображен на рис. 2.
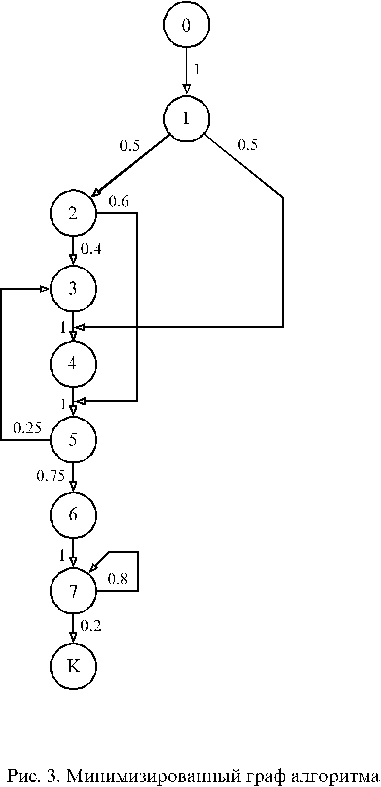
Граф алгоритма можно существенно упростить, если трудоемкость выполнения логических вершин незначительна по сравнению с трудоем-костью выполнения операторных вершин. Тогда состояния, соответствую-щие логическим вершинам, можно слить с предшествующими им состояния-ми, соответствующими операторным вершинам. В нашем примере можно слить состояния (1,2), (3,4), (7,8), (10,11). После вполне понятной перенумера-ции получим минимизированный граф алгоритма, изображенный на рис. 3. При достаточном опыте к нему можно было прийти сразу от схемы алгорит-ма, приведенной на рис. 1.
Обозначим через 
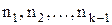 среднее число обращений к операторам
среднее число обращений к операторам 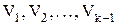 соответственно. Каждый из операторов
соответственно. Каждый из операторов 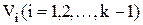 будем характеризовать следующим набором чисел:
будем характеризовать следующим набором чисел:
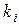 -среднее количество процессорных операций, выполняемых в операторе
-среднее количество процессорных операций, выполняемых в операторе 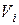 ;
;
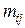 - среднее количество обращений к файлу
- среднее количество обращений к файлу 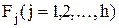 из оператора
из оператора 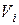 ;
;
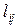 - среднее количество информации, передаваемое при одном обращении к файлу
- среднее количество информации, передаваемое при одном обращении к файлу 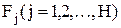 из оператора
из оператора 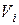 .
.
Тогда трудоемкость алгоритма может быть оценена по следующим формулам:
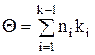 ; (1)
; (1)
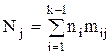 ; (2)
; (2)
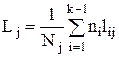 ,
, 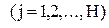 (3)
(3)
где 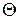 - среднее число процессорных операций, выполняемых при одном прогоне алгоритма;
- среднее число процессорных операций, выполняемых при одном прогоне алгоритма;
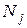 - среднее число обращений к файлу
- среднее число обращений к файлу 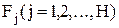 за один прогон алгоритма;
за один прогон алгоритма;
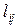 - среднее количество информации, передаваемое при каждом обращении к файлу
- среднее количество информации, передаваемое при каждом обращении к файлу 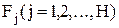 , при одном прогоне программы.
, при одном прогоне программы.
Для определения среднего числа обращений ni к оператору Vi (i=1,2,...,k-1) обычно делаются следующие допущения:
- вероятность выполнения после оператора Vi оператора Vj равна Pij и является постоянной величиной;
- вероятность Pij зависит только от оператора Vi, но никак не связана со способом попадания в оператор Vj, т.е. не зависит от предыстории вычислительного процесса;
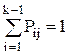 .
.
При выполнении вышеуказанных допущений вычислительный процесс является марковским процессом с состояниями S1,S2,...,Sk. При этом операторы V1,V2,...,Vk-1 соответствуют состояниям S1,S2,...,Sk-1. Состояние Sk соответствует конечной вершине графа алгоритма и является поглощающим, т.е. при достижении состояния процесс прекращается. Состояния S1,S2,...,Sk-1 называются невозвратными, так как процесс непременно их покидает.
В настоящее время существует несколько способов оценки трудоемкости алгоритма. Рассмотрим некоторые из них.
Оценка трудоемкости алгоритмов методами
теории марковских цепей
Для определения среднего числа процессорных операций, выполняемых за один прогон программы, следует граф алгоритма записать в виде стохастической матрицы P. Для рис.3 она примет вид:
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | Sk | |
| S0 | ||||||||
| S1 | 0.5 | 0.5 | ||||||
| S2 | 0.4 | 0.6 | ||||||
| S3 | ||||||||
| S4 | ||||||||
| S5 | 0.25 | 0.75 | ||||||
| S6 | ||||||||
| S7 | 0.8 | 0.2 |
Элементами матрицы P являются вероятности перехода из состояния i в состояние j, которые приведены на графе алгоритма.
Из стохастической матрицы следует, например, что в состоянии S4 процесс может оказаться при переходе из S1 с вероятностью 0.5 или при переходе из состояния S3 с вероятностью 1. Если известны средние числа обращений к вершинам V1 и V3 , то число обращений к вершине V4 будет соответственно равно:
n4 = p14 n1 + p34 n3 = 0.9n1 + n3 .
В самом общем случае можно записать ( суммирование по столбцу стохастической матрицы ):
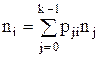 , (n0 = 1, i = 1,2,...,k-1). (4)
, (n0 = 1, i = 1,2,...,k-1). (4)
Последняя запись представляет собой систему линейных алгебраических уравнений, решение которых даст искомое среднее число обращений к операторам.
Для примера из стохастической матрицы имеем:
n1 = 1n0 = 1*1 = 1 ;
n2 = 0.5n1 = 0.5*1 = 0.5 ;
n3 = 0.4n2 + 0.25n5 = 0.2 + 0.25n5 ;
n4 = 0.5n1 + n3 = 0.5 + n3 ;
n5 = 0.6n2 + n4 = 0.3 + n4 ;
n6 = 0.75n5 ;
n7 = n6 + 0.8n7 .
Решая систему уравнений, получим:
n1 = 1; n2 = 0.5; n3 = 0.533; n4 = 1.033;
n5 = 1.333; n6 = 1; n7 = 5.
Для проверки правильности решения системы линейных уравнений можно использовать очевидное тождество:
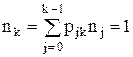 , при n0 = 1. (5)
, при n0 = 1. (5)
В приведенном примере это выполняется так: nk = 0.2 * n7 = 0.2 * 5 = 1.
Данный метод является универсальным ( в случае марковского процесса ), но требует больших затрат времени при значительных размерах стохастической матрицы.
Сетевой подход к оценке трудоемкости алгоритмов
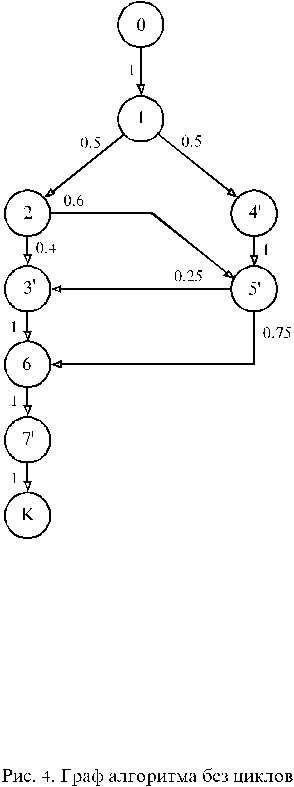
Сетевой подход удобен для анализа вручную и позволяет вычислять среднюю, минимальную и максимальную трудоемкость алгоритма на графах, не содержащих циклы. Для примера рассмотрим граф алгоритма, изображенный на рис.4. Воспользовавшись формулой (4) для рис.4 можем записать:
n0 = 1 ;
n1 = 1 * n0 = 1 ;
n2 = 0.5 * n1 = 0.5 ;
n4’ = 0.5 * n1 = 0.5 ;
n5’ = n4’ + 0.6n2 = 0.5 + 0.6 * 0.2 = 0.8 ;
n3’ = 0.4n2 + 0.25n5’ = 0.4 * 0.5 + 0.25 * 0.8 =0.4 ;
n6 = n3’ + 0.75n5’ = 0.4 + 0.75 * 0.8 = 1 ;
n7’ = 1 * n6 =1 .
За счет отсутствия циклов система оказывается легко разрешимой. Затраты времени на анализ могут быть снижены дополнительно, если ввести эффективную нумерацию состояний графа алгоритма. Последняя заключается в том, что номер вершины должен быть таким, чтобы входящие в эту вершину дуги начинались в вершинах с меньшими номерами. Если после такой нумерации уравнения записывать в порядке возрастания их номеров, то они будут сразу решаться, так как неизвестные с меньшими номерами будут уже вычислены. В приведенном примере нумерация вершин не соответствует указанному требованию, но уравнения записывались в порядке их решения.
При наличии в графе алгоритма циклов последние следует заменить операторами с эквивалентной трудоемкостью. Если в графе алгоритма имеются циклы в цикле, то, очевидно, первоначально следует заменить эквивалентными операторами внутренние циклы, а затем переходить к замене внешних циклов. Расчет трудоемкости алгоритма выполняется по вышеприведенной методике.
Обозначим через pc вероятность замыкания цикла, т. е. вероятность перехода по дуге из конца цикла в его начало. Тогда в соответствии с выражением (4) можно записать :
nc = 1 + pcnc , (6)
где nc - среднее число повторений цикла.
Из выражения (6) имеем:
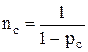 (7)
(7)
Тогда среднее число процессорных операций цикла будет равно :
kc = nckтс ,
где kтс - средняя трудоемкость тела цикла;
kс - средняя трудоемкость цикла.
Среднее число обращений к файлам и среднее количество информации, передаваемое при обращении в цикле к файлам, определяется аналогично.
Рассмотрим пример.
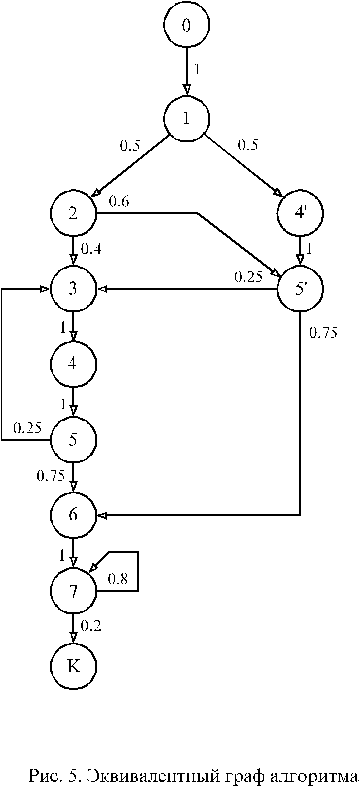
В алгоритме на рис.3 имеется два цикла. Первый содержит операторы V3,V4,V5, а второй состоит только из оператора V7. Первый цикл усложнен входами внутрь цикла из операторов V1 и V2 . Для избавления от входов в цикл не через начало цикла V3 произведем элементарные преобразования графа алгоритма. Эквивалентный граф после очевидных преобразований изображен на рис.5. Из рис.5 следует, что операторы V4 и V5 , которые использовались для входа в тело цикла не через его начало, вынесены отдельно под номерами 4’ и 5’.
Количество повторений циклов из выражения (7) равно :
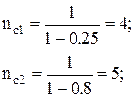
где nc1, nc2 - число повторений первого и второго циклов.
Граф алгоритма без циклов приведен на рис.4.
Вышеприведенный подход позволяет вычислить среднюю трудоемкость алгоритма. Для оценки максимальной и минимальной трудоемкости алгоритма необходимо перебрать все возможные пути, ведущие из начальной вершины графа алгоритма в конечную, и выбрать из них пути, дающие максимальную и минимальную трудоемкость. Следует учесть, что, например, путь с минимальным количеством процессорных операций может иметь не минимально возможное число обращений к файлам. При наличии циклов в графе алгоритма для тела цикла определяется минимальная и максимальная трудоемкость. Находится минимальное и максимальное число повторений цикла и формируются соответствующие эквивалентные по трудоемкости операторы.
В качестве примера оценим минимальное и максимальное число процессорных операций для графа алгоритма, изображенного на рис.4. Для упрощения примем, что все операторы имеют трудоемкость, равную 1000 процессорных операций. Через Ai и Bi будем обозначать соответственно минимальное и максимальное число процессорных операций, которое будет иметь место в момент выхода процесса из i-й вершины графа.
A0 = 0; B0 = 0;
A1 = min(A0) + 1000 = 1000; B1 = max(B0) + 1000 = 1000;
A2 = min(A1) + 1000 = 2000; B2 = max(B1) + 1000 = 2000;
A4’ = min(A1) + 1000 = 2000; B4’ = max(B1) + 1000 = 2000;
A5’ = min(A2,A4’) + 1000 = 3000; B5’ = max(B2,B4’) + 1000 = 3000;
A3’ = min(A2,A5’) + 1000 = 3000; B3’ = max(B2,B5’) + 1000 = 4000;
A6 = min(A3’,A5’) + 1000 = 4000; B6 = max(B3’,B5’) + 1000 = 5000;
A7 = min(A6) + 1000 = 5000; B7 = max(B6) + 1000 = 6000.
Порядок выполнения работы
1. Из табл.1 выбирается логическая схема алгоритма (ЛСА) в соответствии с вариантом. По ЛСА изображается графическая схема алгоритма. В ЛСА символам Нач. и Кон. соответствуют начальный и конечный операторы алгоритма. Символами A, B, C, D, E, K, M обозначены функциональные операторы алгоритма. Символами x1, x2, x3, x4 обозначены логические условия. Если логическое условие равно единице, то выполняется следующий по порядку оператор в ЛСА. Если логическое условие равно нулю, то осуществляется переход по стрелке с соответствующим индексом. У логического условия стрелка направлена вверх. Например, i . У места перехода стрелка направлена вниз - ¯i.
Для схемы алгоритма, изображенной на рис.1 ЛСА имеет вид :
Нач. Ax11Bx33¯2C¯1D¯3Ex22M¯4Kx44 Кон.
Из табл.2 выбираются вероятности переходов при единичных логических условиях. Из табл.3 находятся количества процессорных операций в операторах алгоритма. Из табл.4 по последней цифре варианта выбираются количество обращений и длина записи в килобайтах при обращении к файлам F1, F2, F3.
2. Изображается схема алгоритма, граф алгоритма и минимальный граф алгоритма.
3. Определяется трудоемкость алгоритма методами теории марковских цепей.
4. Определяется средняя трудоемкость алгоритма с помощью сетевого подхода.
5. Вычисляется минимальная и максимальная трудоемкость алгоритма.
6. Полученные результаты анализируются и оформляются в виде отчета.
Контрольные вопросы
1. Что такое трудоемкость алгоритма ?
2. Что такое сложность алгоритма ?
3. Как определяется сложность алгоритма и в каких случаях требуется эта оценка ?
4. Как определяется трудоемкость алгоритма и с какой целью вычисляется эта величина ?
5. Почему трудоемкость алгоритма является, как правило, случайной величиной ?
6. Какие параметры могут быть использованы для характеристики трудоемкости алгоритма ?
7. Как выполнить эффективную нумерацию состояний в графе алгоритма для сетевого анализа ?
8. Что такое стохастическая матрица ?
9. Как определить вероятности выхода из логической вершины ? Привести примеры.
10.Что такое марковский процесс ?
11.Зачем делается допущение о вычислительном процессе как марковском при оценке трудоемкости алгоритма ?
12.Докажите правильность формулы (4).
13.Докажите правильность тождества (5).
14.Докажите правильность выражения (6).
15.Существует ли разность в оценке средней трудоемкости при использовании методов теории марковских цепей и сетевого подхода ? Объясните ее.
Литература
Основы теории вычислительных систем / Под ред. С.А. Майорова. - М.: Высшая школа, 1978. - 408 стр.
Таблица 1 -Варианты схем алгоритмов
| Вариант | Логическая схема алгоритма. |
| Нач. Ax11Bx22C¯3x33D¯2E¯4Mx44K¯1 Кон. | |
| Нач. Ax22Bx33x11D¯3E¯1¯3M¯2x33K Кон. | |
| Нач. Ax22B¯3¯2Cx33¯1Dx11Ex44MK¯4 Кон. | |
| Нач. A¯2¯1Bx11Cx22Dx44¯5Ex33M¯4K Кон. | |
| Нач. ¯1Ax11Bx22Ex33C¯2¯3Mx44D¯4K Кон. | |
| Нач. ¯4Bx22Cx33D¯2¯3Ex44Mx11K¯1 Кон. | |
| Нач. Ax22Cx44Dx33E¯2¯3¯4Kx44MB Кон. | |
| Нач. Dx11Ex22M¯2¯3Ax22Mx33K¯1D Кон. | |
| Нач. x11A¯1¯2Bx22C¯4Dx33K¯3Mx44 Кон. | |
| Нач. x11A¯4¯2Bx22Cx33E¯3Dx44K¯1M Кон. | |
| Нач. ¯3Ax11Bx22C¯2D¯1Ex33Kx44M¯4 Кон. | |
| Нач. x44Ax11B¯2Cx22D¯1Ex33K¯4M¯3x11 Кон. | |
| Нач. Ax11Bx22C¯2¯1D¯3¯4EKx44Mx33 Кон. | |
| Нач. ¯5Ax11Bx22C¯2D¯3Ex33C¯1DEx33Kx44M¯4 Кон. | |
| Нач. ¯2Ax11B¯1Cx22DEx33K¯3Mx22 Кон. | |
| Нач. ¯1Ax11B¯4¯2Cx22Dx44Ex22Kx33M¯3 Кон. | |
| Нач. ¯1Ax11Bx33C¯3Dx44E¯2Kx22M¯4 Кон. | |
| Нач. ¯4Ax44Bx11C¯1Dx33Ex22K¯2M¯3 Кон. | |
| Нач. x11A¯3Bx22Cx44D¯2¯4Ex33KM¯4 Кон. | |
| Нач. ¯4Ax11B¯1C¯2¯3Dx11Ex22Kx33Mx44 Кон. | |
| Нач. x11A¯3Bx22Cx44D¯4E¯2K¯1Mx33 Кон. | |
| Нач. x22A¯3Bx11C¯2Dx44E¯1¯4KMx33 Кон. | |
| Нач. x11Ax22B¯2¯1Cx44D¯3Ex33KM¯4 Кон. | |
| Нач. x11A¯2B¯1Cx22D¯3Ex33¯4Mx44 Кон. | |
| Нач. x33Ax22¯1Bx11C¯2¯3D¯4Ex44MK Кон. |
Таблица 2 - Вероятности перехода ( по Х=1 )
| Вариант | P1 | P2 | P3 | P4 |
| 0.1 | 0.3 | 0.6 | 0.9 | |
| 0.2 | 0.2 | 0.7 | 0.8 | |
| 0.3 | 0.1 | 0.8 | 0.7 | |
| 0.4 | 0.2 | 0.9 | 0.6 | |
| 0.5 | 0.3 | 0.8 | 0.5 | |
| 0.6 | 0.4 | 0.7 | 0.4 | |
| 0.7 | 0.5 | 0.6 | 0.3 | |
| 0.8 | 0.6 | 0.5 | 0.2 | |
| 0.9 | 0.7 | 0.4 | 0.1 | |
| 0.8 | 0.8 | 0.3 | 0.2 | |
| 0.7 | 0.9 | 0.2 | 0.3 | |
| 0.6 | 0.8 | 0.1 | 0.4 | |
| 0.5 | 0.7 | 0.2 | 0.5 | |
| 0.4 | 0.6 | 0.3 | 0.4 | |
| 0.3 | 0.5 | 0.4 | 0.3 | |
| 0.2 | 0.4 | 0.5 | 0.2 | |
| 0.1 | 0.3 | 0.6 | 0.1 | |
| 0.2 | 0.2 | 0.7 | 0.2 | |
| 0.3 | 0.1 | 0.8 | 0.3 | |
| 0.4 | 0.2 | 0.9 | 0.4 | |
| 0.5 | 0.3 | 0.8 | 0.5 | |
| 0.6 | 0.4 | 0.7 | 0.6 | |
| 0.7 | 0.5 | 0.6 | 0.7 | |
| 0.8 | 0.6 | 0.5 | 0.8 | |
| 0.9 | 0.7 | 0.4 | 0.9 |
Таблица 3 - Количество процессорных операций в операторах (в тысячах)
| № п/п | A | B | C | D | E | M | K |
Таблица 4 - Количество обращений к файлам ( числитель ) и длина записи в килобайтах ( знаменатель )
| № | A | B | C | D | E | M | K | |||||||||||
| п/п | F1 | F2 | F1 | F2 | F3 | F1 | F2 | F3 | F1 | F2 | F1 | F2 | F3 | F1 | F2 | F3 | F1 | F2 |
| 0/0 | 1/1 | 2/2 | 3/3 | 4/4 | 3/5 | 2/6 | 1/7 | 0/0 | 1/8 | 2/9 | 3/8 | 4/7 | 3/6 | 2/5 | 1/4 | 0/0 | 1/3 | |
| 2/2 | 3/1 | 4/2 | 3/3 | 2/4 | 1/5 | 0/0 | 1/6 | 2/7 | 3/6 | 4/9 | 3/8 | 2/7 | 1/6 | 0/0 | 1/5 | 2/4 | 3/3 | |
| 4/2 | 0/0 | 1/1 | 2/2 | 3/3 | 4/4 | 3/5 | 2/6 | 1/7 | 0/0 | 1/8 | 2/9 | 3/8 | 4/7 | 3/6 | 2/5 | 1/4 | 0/0 | |
| 1/3 | 2/2 | 3/1 | 4/2 | 3/3 | 2/4 | 1/5 | 0/0 | 1/6 | 2/7 | 3/8 | 4/9 | 3/8 | 2/7 | 1/6 | 0/0 | 1/5 | 2/4 | |
| 3/3 | 4/2 | 3/1 | 2/2 | 1/3 | 0/0 | 1/4 | 2/5 | 3/6 | 4/7 | 3/8 | 2/9 | 1/1 | 0/0 | 1/2 | 2/3 | 3/4 | 4/5 | |
| 1/6 | 0/0 | 1/7 | 2/8 | 3/9 | 4/8 | 3/7 | 2/6 | 1/5 | 0/0 | 2/4 | 3/3 | 4/2 | 3/1 | 2/2 | 1/3 | 0/0 | 1/4 | |
| 2/5 | 1/6 | 0/0 | 1/7 | 2/8 | 3/9 | 4/8 | 3/7 | 2/6 | 1/5 | 0/0 | 1/4 | 2/3 | 3/2 | 4/1 | 3/2 | 2/3 | 1/4 | |
| 0/0 | 2/5 | 3/6 | 1/7 | 2/8 | 3/9 | 4/8 | 3/7 | 2/6 | 1/5 | 0/0 | 1/4 | 2/3 | 3/2 | 4/1 | 3/2 | 2/3 | 1/4 | |
| 4/5 | 3/6 | 2/7 | 1/8 | 0/0 | 1/9 | 2/8 | 3/7 | 4/6 | 3/5 | 2/4 | 1/3 | 0/0 | 1/2 | 2/1 | 3/2 | 4/3 | 3/4 | |
| 2/5 | 1/6 | 0/0 | 1/7 | 2/8 | 3/9 | 4/8 | 0/0 | 1/7 | 2/6 | 3/5 | 4/4 | 3/3 | 2/2 | 1/1 | 0/0 | 1/2 | 2/3 |
|
из
5.00
|
Обсуждение в статье: ОЦЕНКА ТРУДОЕМКОСТИ АЛГОРИТМА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

