I. Определение Гамильтонова пути в графе

2015-11-12

556

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 12

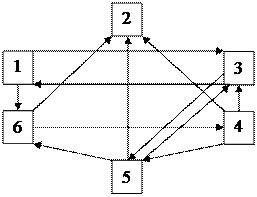1.1 Для заданного графически, ориентированного графа составить матрицу смежности R с единицами на главной диагонали (матрица достижимости за один шаг).

1.2 Найти ГП в графе, используя алгоритм Фаулкса (алгоритм выполнения смотри в теоретической части).

Рассмотрев матрицу R, мы не нашли ни одной начальной и ни одной конечной вершины. Переходим к следующему циклу.

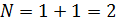
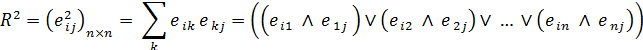
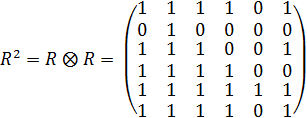
Рассмотрев матрицу R², замечаем, что вершина №2 есть конечная вершина гамильтонова пути на данном цикле вычислений.

Это свойство выражается наличием единиц во всем столбце №2 и нулей во всей строке №2 (за исключением их пересечения).

Так же заметим, что вершина №5 есть начальная вершина гамильтонова пути на данном цикле вычислений.

Это свойство выражается наличием единиц во всей строке №5 и нулей во всем столбце №5 (за исключением их пересечения).

Упростив матрицу R², за счет вычеркивания строк и столбцов №2 и №5, получаем матрицу:

То же проделываем и с начальной матрицей R, получаем:

Так как 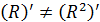, переходим к :

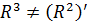
Все элементы , равны единице. Следовательно, что и и и т.д. будут равны, то есть будут иметь все элементы равные единице.

Путем возвращения вычеркнутых строк и столбцов получаем матрицу:

Группируем матрицу так, чтобы все нули были расположены под главной диагональю, а единицы – над ней:

R^c =

Нами получено три класса эквивалентности:

1. вершина – 5;

2. вершины – 1, 3, 4, 6;

3. вершина – 2.

Таким образом, гамильтонов путь может быть таким:

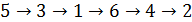
Алгоритм Фаулкса в общем случае не решает однозначно задачу нахождения гамильтонова пути, он только частично упорядочивает множество вершин, снижая тем самым размерность решаемой задачи.

В случае, когда в каждый класс эквивалентности входит одна вершина, алгоритм Фаулкса определяет Гамильтонов путь однозначно.

II. Поиск Эйлерова пути (ЭП) в графе.

1.1 Для заданного графически неориентированного графа составить матрицу смежности с единицами на главной диагонали (матрица достижимости за один шаг).

№

R =

3

1.2 Найти Эйлеров путь в графе, используя алгоритм, приведенный в теоретической части.

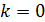. Эйлеров путь существует, так как степени всех вершин четные. Выберем начальную вершину №1, то есть 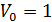. Число непомеченных ребер .

. С вершиной №1 связаны вершины №2 и №5. . Следующей вершиной Эйлерова пути является вершина №2. Ребро помечается.

. С вершиной №2 связаны вершины №3, №5 и №6. . Следующей вершиной Эйлерова пути является вершина №3. Ребро помечается.

. С вершиной №3 связаны вершины №4, №5 и №6. 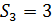. Следующей вершиной Эйлерова пути является вершина №4. Ребро 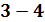помечается.

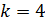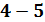. С вершиной №4 связаны вершина №5. . Следующей вершиной Эйлерова пути является вершина №5. Ребро помечается.

. С вершиной №5 связаны вершины №1, №2 и №3. . Следующей вершиной Эйлерова пути является вершина №1. Ребро помечается.

. Нет вершин связанных с вершиной №1 непомеченными ребрами. . Получен цикл .

Вершины №2, №3 и №5, входящие в этот цикл, имеют непомеченные ребра. Рассмотрим вершину №2 в качестве начальной точки следующего цикла.

. С вершиной №2 связаны вершины №5 и №6. . Следующей вершиной Эйлерова пути является вершина №5. Ребро помечается.

. С вершиной №5 связана вершина №3. . Следующей вершиной Эйлерова пути является вершина №3. Ребро помечается.

. С вершиной №3 связана вершина №6. 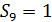. Следующей вершиной Эйлерова пути является вершина №6. Ребро помечается.

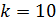. С вершиной №6 связана вершина №2. . Следующей вершиной Эйлерова пути является вершина №2. Ребро помечается.

. Нет вершин связанных с вершиной №2 непомеченными ребрами. 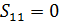. Получен цикл .

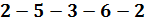В найденных циклах не осталось вершин с непомеченными ребрами. Следовательно работа алгоритма завершена.Для нахождения Эйлерова пути необходимо объединить найденные циклы:

1. ;

2. .

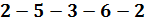Объединив циклы в вершине №2 получаем Эйлеров путь:

1.3 Найти Эйлеров путь в графе для начальной вершины, выбранной в пункте №2, используя стандартную программу на ЭВМ.

№

R =

3

Эйлеровы пути:

1) 1―2―3―4―5―2―6―3―5―1

2) 1―2―3―4―5―3―6―2―5―1

3) 1―2―3―5―2―6―3―4―5―1

4) 1―2―3―5―4―3―6―2―5―1

5) 1―2―3―6―2―5―3―4―5―1

6) 1―2―3―6―2―5―4―3―5―1

7) 1―2―5―3―2―6―3―4―5―1

8) 1―2―5―3―6―2―3―4―5―1

9) 1―2―5―4―3―2―6―3―5―1

10) 1―2―5―4―3―6―2―3―5―1

11) 1―2―6―3―2―5―3―4―5―1

12) 1―2―6―3―2―5―4―3―5―1

13) 1―2―6―3―4―5―2―3―5―1

14) 1―2―6―3―4―5―3―2―5―1

15) 1―2―6―3―5―2―3―4―5―1

16) 1―2―6―3―5―4―3―2―5―1

17) 1―5―2―3―4―5―3―6―2―1

18) 1―5―2―3―5―4―3―6―2―1

19) 1―5―2―6―3―4―5―3―2―1

20) 1―5―2―6―3―5―4―3―2―1

21) 1―5―3―2―5―4―3―6―2―1

22) 1―5―3―2―6―3―4―5―2―1

23) 1―5―3―4―5―2―3―6―2―1

24) 1―5―3―4―5―2―6―3―2―1

25) 1―5―3―6―2―3―4―5―2―1

26) 1―5―3―6―2―5―4―3―2―1

27) 1―5―4―3―2―5―3―6―2―1

28) 1―5―4―3―2―6―3―5―2―1

29) 1―5―4―3―5―2―3―6―2―1

30) 1―5―4―3―5―2―6―3―2―1

31) 1―5―4―3―6―2―3―5―2―1

32) 1―5―4―3―6―2―5―3―2―1