Правила вычисления погрешностей

В практической деятельности человеку приходится измерять различные величины, учитывать материалы и продукты труда, производить различные вычисления. Результатами различных измерений, подсчетов и вычислений являются числа. Однако точные измерения невозможны ввиду несовершенства наших органов зрения, неточности измерительных приборов и некоторых свойств самих измеряемых объектов.

При различных измерениях одной и той же величины получают различные приближенные значения. Каждое из этих приближений отличается от истинного значения на некоторую величину, называемую погрешностью.

I Абсолютной погрешностью называется модуль разности истинного и приближенного значения некоторой величины, обозначается буквой и измеряется в тех же единицах, что и вычисляемая величина.

Из этого определения следует, что истинное значение величины равно приближенному значению абсолютная погрешность .

Абсолютная погрешность приближения не характеризует качества измерений, т.к., например, точность 1 см для определения ширины футбольного поля является высокой, а для определения длины карандаша - низкой. Поэтому для характеристики точности измерения вводится понятие относительной погрешности.

Если в расчетной формуле используется табличное значение, то его абсолютная погрешность определяется следующем образом: берется последняя цифра числа и приравнивается единице.

Пример: плотность воды

Поверхностное натяжение воды

II Относительной погрешностью приближения называется отношение абсолютной погрешности приближения к модулю числа приближенного значения и обозначается буквой (эпсилон)

где x – приближенное значение некоторой величины.

Погрешность приближенного равенства x очень мала по сравнению с погрешностью x. Поэтому при оценке абсолютной погрешности x можно считать, что x=dx, где dx-дифференциал (производная) величины x.

1) Относительная погрешность произведения не превышает суммы относительных погрешностей ее сомножителей.

X=U*V; , т. е.

;откуда

абсолютная погрешность величины х равна

Во всех остальных случаях (после расчёта относительной погрешности) абсолютная погрешность вычисляется по этой же формуле.

2) Относительная погрешность степени равна относительной погрешности основания, умноженной на показатель степени.

;

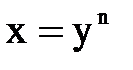3) Относительная погрешность корня равна относительной погрешности подкоренного числа, деленной на показатель степени корня.

;

4)Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

X=U/V;

5) Относительная погрешность суммы равна сумме относительных погрешностей слагаемых.

X=U+V;

6) Относительная погрешность разности не превышает суммы

погрешностей уменьшаемого и вычитаемого.

X=U – V;

Исключение составляет случай, когда разность находится в знаменателе дробного выражения.

Пример 1:

X= ;

Пример 2:

X= ; .

Окончательный результат вычислений записывается системой

x и измеряются в одних и тех же единицах, а - в процентах.

Относительная погрешность высчитывается для всех физических величин, стоящих в формуле.

III Абсолютная погрешность непосредственно измеренных величин (систематическая погрешность приборов) равна половине цены деления шкалы прибора.

IV Погрешность констант (табличных значений) равна половине их абсолютной погрешности.