 |
Главная |
Применения скалярного произведения
|
из
5.00
|
ВЕКТОРЫ
Вектор - направленный отрезок.  =
=  - длина вектора. Если
- длина вектора. Если  =1, то
=1, то  - единичный вектор.
- единичный вектор.
Коллинеарными (  )называют векторы, расположенные
)называют векторы, расположенные  на параллельных (в частности, на одной) прямых, а компланарными– векторы, расположенные в параллельных (в частности, в одной) плоскостях.
на параллельных (в частности, на одной) прямых, а компланарными– векторы, расположенные в параллельных (в частности, в одной) плоскостях.
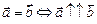 (коллинеарны и одинаково направлены - сонаправлены) и
(коллинеарны и одинаково направлены - сонаправлены) и  .
.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, перемещая начало  в любую другую точку на плоскости или в пространстве. Такие векторы называются свободными.
в любую другую точку на плоскости или в пространстве. Такие векторы называются свободными.
Линейные операции над геометрическими векторами
Сумма 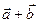

|    Правило треугольника Правило параллелограмма Разность
Правило треугольника Правило параллелограмма Разность 
|
Умножение на число:  .
1. .
1. 
 2.
2. 
|  
 ; ;  ; ;  ; ;  . .
|
Линейная зависимость и независимость векторов. Базис
Вектор  , где
, где 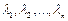 – произвольные действительные числа, называется линейной комбинацией векторов
– произвольные действительные числа, называется линейной комбинацией векторов 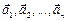 .
.
Система векторов 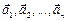 линейно зависима, если, по крайней мере, один из них является линейной комбинацией остальных. В противном случае линейно независимы. Например, если
линейно зависима, если, по крайней мере, один из них является линейной комбинацией остальных. В противном случае линейно независимы. Например, если  , то векторы
, то векторы 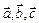 линейно зависимы.
линейно зависимы.
Любые  линейно независимых векторов пространства
линейно независимых векторов пространства  называют базисом этого пространства. Если эти векторы единичные и попарно перпендикулярные, то базис называется ортонормированным.
называют базисом этого пространства. Если эти векторы единичные и попарно перпендикулярные, то базис называется ортонормированным.
Базис на плоскости (в  )
образуют любые два неколлинеарные вектора )
образуют любые два неколлинеарные вектора
  и и   
| Ортонормированный базис в  - -
 три попарно перпендикулярных единичных вектора три попарно перпендикулярных единичных вектора  : :  Разложение вектора по базису
Разложение вектора по базису
 , ,
 , ,  , ,  – координаты вектора.
Обозначение: – координаты вектора.
Обозначение: 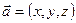
|
Базис в пространстве (в  )
образуют любые три некомпланарных вектора )
образуют любые три некомпланарных вектора  
|
| Проекция вектора на ось | Прямоугольная декартова система координат (ПДСК) | |
 пр
пр
|   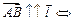 пр пр 
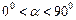  пр пр 
   пр пр 
  пр пр 
  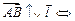 пр пр 
| 
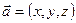  , ,
 – абсцисса, – абсцисса,  – ордината, – ордината,  – аппликата. – аппликата.
|
ВПДСК:  пр
пр 
 пр
пр 
 пр
пр  где
где  – углы, которые составляет вектор
– углы, которые составляет вектор  с координатными осями
с координатными осями  соответственно;
соответственно;  называются направляющими косинусами вектора
называются направляющими косинусами вектора  :
:  .
.
 единичный вектор, сонаправленный с вектором
единичный вектор, сонаправленный с вектором  ,– орт вектора
,– орт вектора 
(нормированный вектор).
Если даны точки А  и В и В  , то , то
| ||
координаты вектора 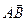
| координаты середины М отрезка АВ | длина отрезка АВ (модуль вектора 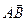 ) )
|

| 
| 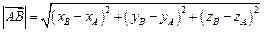
|
Если векторы заданы координатами 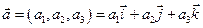 и и  , то , то
| |||
| модуль вектора | Линейные операции | Равенство векторов | Коллинеарность |
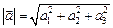
|   

|
  
|   

|
Скалярное произведение двух векторов (обозначение: 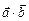 или
или 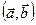 )
)
| По определению | В проекцииях | В координатах | Свойства |
Число, равное
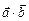 = = 
| 
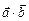 = = 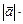 пр пр  = =  пр пр 
|
 =
= 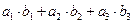
| 1) 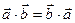 ; 2) ; 2)  ;
3) ;
3)  ;
4) ;
4)  ; 5) ; 5)  . .
|
Применения скалярного произведения
| Модуль вектора | Угол между векторами | Условие ортогональности | Вычисление проекций | Вычисление работы силы |


| 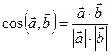 =
= =
= 
|
  

|
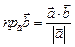
| 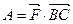

|
Полярные координаты точки  :
:  радиус-вектор точки М,
радиус-вектор точки М,  полярный радиус,
полярный радиус,  полярный угол,
полярный угол,


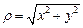

 Пример: Найти полярные координаты точки
Пример: Найти полярные координаты точки  , если ее декартовы координаты
, если ее декартовы координаты  .
.
Решение.  ,
, 
|
из
5.00
|
Обсуждение в статье: Применения скалярного произведения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

