 |
Главная |
ТЕМА «Определенный интеграл»
|
из
5.00
|
Вычислить интегралы:
1.  ; 2.
; 2. 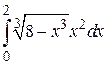 ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 
6. 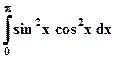 ; 7.
; 7.  .
.
Вычислить несобственные интегралы или установить их расходимость:
8.  ; 9.
; 9.  .
.
Вычислить площадь фигуры, ограниченной линиями:
10.  11.3x+2y–6 = 0, 3x2–2y = 0, y = 0.
11.3x+2y–6 = 0, 3x2–2y = 0, y = 0.
12. Вычислить длину дуги кривой, заданной параметрически:

13. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями  вокруг оси OY.
вокруг оси OY.
ТЕМА «Дифференциальные уравнения»
- Найти общее решение (общий интеграл) дифференциального уравнения:
а)  ; b)
; b)  ; c)
; c)  .
.
- Найти частное решение (частный интеграл) дифференциального уравнения:
 .
.
- Найти общее решение дифференциального уравнения:
 .
.
- Найти частное решение дифференциального уравнения и вычислить значение полученной функции
 при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
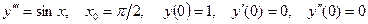 .
.
- Найти общее решение дифференциального уравнения, допускающего понижение порядка:
 .
.
- Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка:
 .
.
- Проинтегрировать следующее уравнение:
 .
.
- Найти общее решение ЛОДУ второго порядка.
1.  2.
2.  3.
3. 
- Найти частное решение ДУ
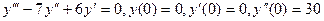
- Определить и записать структуру частного решения
 ЛНДУ по виду функции f(x):
ЛНДУ по виду функции f(x):


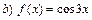
- Найти общее решение ЛНДУ
 ;
;  ;
; 
- Найти общее решение ЛНДУ методом вариации постоянных
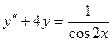 .
. - Решить систему дифференциальных уравнений

- Найти общее решение (общий интеграл) дифференциального уравнения:
а)  ; b)
; b) 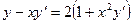 ; c)
; c)  .
.
2. Найти частное решение (частный интеграл) дифференциального уравнения:
 .
.
- Найти общее решение дифференциального уравнения:
 .
.
- Найти частное решение дифференциального уравнения и вычислить значение полученной функции
 при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
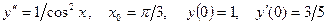 .
.
- Найти общее решение дифференциального уравнения, допускающего понижение порядка:
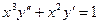 .
.
- Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка:
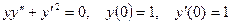 .
.
- Проинтегрировать следующее уравнение:
 .
.
- Найти общее решение ЛОДУ второго порядка.
1.  2.
2.  3.
3. 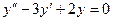
- Найти частное решение ДУ

- Определить и записать структуру частного решения
 ЛНДУ по виду функции f(x):
ЛНДУ по виду функции f(x):



- Найти общее решение ЛНДУ
 ;
;  ;
; 
- Найти общее решение ЛНДУ методом вариации постоянных
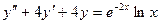 .
.
- Решить систему дифференциальных уравнений

Вариант 1
- Пусть
 ; чему равно
; чему равно  ?
? - Если
 , то значение производной
, то значение производной  равно (выбрать правильный ответ)
равно (выбрать правильный ответ)
1)  2)
2)  3)
3)  4)
4)  5)
5) 
- Найдите первую производную для частного
 двух функций
двух функций  и
и  .
. - Результат вычисления значения первой производной функции
 в точке
в точке  равен (выбрать правильный ответ)
равен (выбрать правильный ответ)
1) 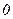 2)
2)  3)
3)  4)
4)  5)
5)  .
.
- Производная функции
 имеет вид (выбрать правильный ответ)
имеет вид (выбрать правильный ответ)
1)  2)
2) 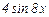 3)
3)  4)
4)  5)
5)  .
.
- Запишите уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой  .
. - Результат вычисления интеграла
 равен (выбрать правильный ответ)
равен (выбрать правильный ответ)
1) 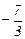 2)
2)  3)
3)  4)
4)  5)
5) 
- Интеграл
 равен (выбрать правильный ответ)
равен (выбрать правильный ответ)
1)  2)
2) 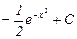 3)
3)  4)
4)  5)
5)  .
.
- Если
 , то результат вычисления значения
, то результат вычисления значения  при
при  равен (выбрать правильный ответ)
равен (выбрать правильный ответ)
1)  2)
2)  3)
3)  4)
4)  5)
5) 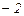 .
.
- Найдите неопределенный интеграл
 .
. - Найдите неопределенный интеграл
 .
. - Площадь фигуры, ограниченной параболой
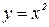 и отрезками прямых
и отрезками прямых  и
и  , равна (выбрать правильный ответ)
, равна (выбрать правильный ответ)
1)  2)
2)  3)
3)  4)
4)  5)
5)  .
.
Вариант экзаменационного теста
- Вычислить:
 .
. - Найти градиент функции
 в точке
в точке  и вычислить его модуль. Найти производную этой функции в точке в направлении вектора
и вычислить его модуль. Найти производную этой функции в точке в направлении вектора  , если
, если  .
.
3. Вычислить: 
- Вычислить (с точностью до двух знаков после запятой) длину дуги данной линии
 между точками
между точками  и
и  . Изобразить данную линию.
. Изобразить данную линию.
5. Найти общее решение: 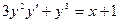
6. Найти общее решение: 
7. Найти общее решение: 
|
из
5.00
|
Обсуждение в статье: ТЕМА «Определенный интеграл» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

