Угловая скорость и угловое ускорение. Вычисление угла поворота тела при равномерном и равноускоренном вращении. Связь линейных и угловых характеристик

Перемещение, скорость, путь, ускорение. Вычисление пройденного пути при равномерном и равноускоренном прямолинейном движении.

Путь – расстояние, которое проходит точка (тело) вдоль траектории. Перемещение – вектор, соединяющий начальную и конечную точки на траектории. Кинематическое уравнение движения материальной точки представляет собой зависимость радиуса - вектора точки от времени .

Мгновенная скорость, средняя скорость (перемещения) и средняя путевая скорость выражаются соответственно формулами

, , ,

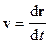где Dr (dr) — перемещение, а Ds — путь, пройденный точкой за интервал времени Dt (dt).

Величина мгновенной скорости может также быть определена по формуле

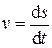
Мгновенное и среднее ускорения

, .

Путь Ds не может убывать и принимать отрицательные значения, т.е. Ds³0. В общем случае путь находят по формуле

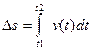
В случае прямолинейного движения с постоянным ускорением (a=const) справедлива формула

,

где a>0 для случая равноускоренного движения и a<0 для равнозамедленного.

Криволинейное движение. Нормальное и тангенциальное ускорения. Кривизна траектории.

При движении тела по криволинейной траектории скорость тела направлена по касательной к траектории, т.е. может изменятся как по величине так и по направлению.

Полное ускорение тела можно разложить на две взаимно перпендикулярные составляющие – тангенциальное и нормальное ускорения.

Тангенциальное ускорение обусловлено изменением скорости по величине и рассчитывается по формуле

. Направлено вдоль касательной к траектории, т.е. по скорости или противрпрложно ей.

Нормальное ускорение обусловлено изменением скорости по направлению и рассчитывается по формуле

(R – радиус кривизны траектории в рассматриваемой ее точке). Направлено перпендикулярно касательной к траектории, т.е. скорости.

Полное ускорение равно

Угловая скорость и угловое ускорение. Вычисление угла поворота тела при равномерном и равноускоренном вращении. Связь линейных и угловых характеристик

Кинематическое уравнение движения материальной точки по окружности представляет зависимость угла поворота точки от времени .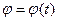

Угловая скорость .

Угловая скорость является псевдовектором (условным вектором). Она параллельна оси вращения точки или тела, а ее направление зависит от направления вращения и определяется правилом правого винта.

Угловое ускорение .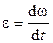

Направлено также как и угловая скорость в случае ускоренного вращения и в противоположную сторону в случае замедленного.

В случае вращения по окружности с постоянным угловым ускорением (ε= const) справедливы формулы

, , ,

где ε>0 для случая равноускоренного движения по окружности и ε<0 для равнозамедленного.

Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:

, , ,

где υ — линейная скорость; a_τ и a_n — тангенциальное и нормальное ускорения; ω — угловая скорость; ε — угловое ускорение; R — радиус окружности.