 |
Главная |
Самостоятельная работа № 2
|
из
5.00
|
Вариант №5
Множественная регрессия
Исходные данные:
| y | x1 | x2 | x3 |
1.Рассчитаем среднеквадратические отклонения и коэффициенты вариации: 
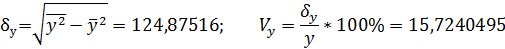
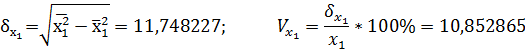
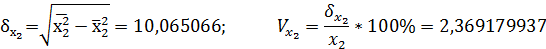
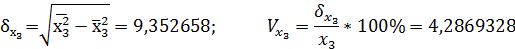
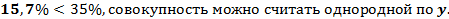
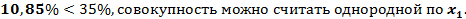

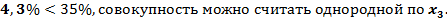
Можно сделать вывод об умеренном варьировании всех признаков.
2. Рассчитаем параметры линейной модели множественной регрессии в чистом виде:
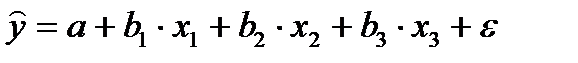 ,
,
МНК для множественной регрессии:
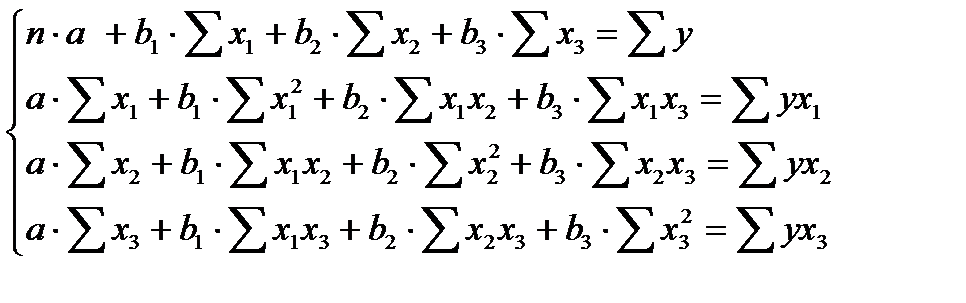
Исходные и расчетные данные:
| y | x1 | x2 | x3 | y2 | x12 | x22 | x32 | |
| Сумма | ||||||||
| Ср.знач | 794,1667 | 108,25 | 424,8333 | 218,1667 | 646294,5 | 11856,083 | 180584,67 | 47684,17 |
| yx1 | yx2 | yx3 | x1x2 | x1x3 | x2x3 | |
| Сумма | ||||||
| Ср.знач. | 85943,33333 | 337854,6 | 172335,8 | 45972,58333 | 23665,41667 | 92687,33333 |

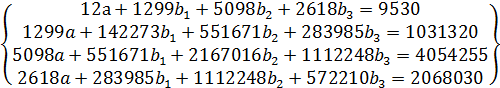
Решим систему методом Крамера:
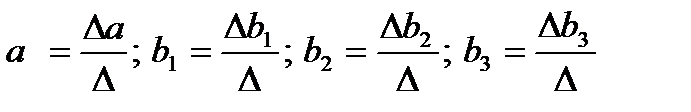 , где
, где
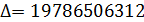
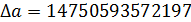
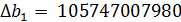
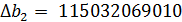
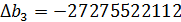
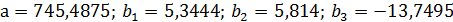
Получили модель: 
В Excel:
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | 745,4875 | 294,7825 | 2,528941 |
| Переменная X 1 | 5,3444 | 0,592119 | 9,025894 |
| Переменная X 2 | 5,813662 | 0,619284 | 9,38771 |
| Переменная X 3 | -13,7495 | 0,737601 | -18,6409 |
3.Рассчитаем парные коэффициенты корреляции и построим матрицу парных коэффициентов корреляции:
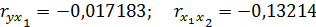
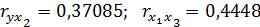
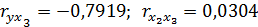
Построим матрицу парных коэффициентов корреляции с помощью Excel:
| y | x1 | x2 | x3 | |
| y | ||||
| x1 | -0,017182872 | |||
| x2 | 0,370848705 | -0,132139017 | ||
| x3 | -0,791890953 | 0,444814942 | 0,030393661 |
Мультиколлинеарности нет: 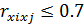
4.Частные коэффициенты корреляции:
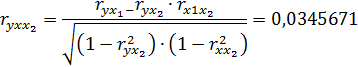
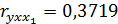
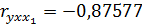
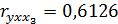
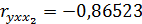
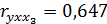
5.Найдем уравнение регрессии в стандартизированном масштабе:
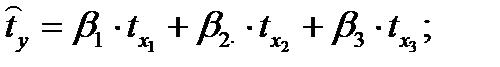
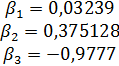
Тогда:
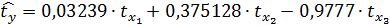
Следовательно, наибольшее влияние на 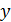 оказывают
оказывают 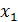 и
и 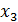 .
.
Коэффициент детерминации:
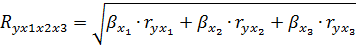
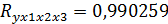
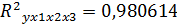
Вариация величины 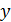 на 99,02% объясняется учтенными факторами в модели, на долю прочих факторов, не учитываемых в модели приходится 0,98%
на 99,02% объясняется учтенными факторами в модели, на долю прочих факторов, не учитываемых в модели приходится 0,98%
Скорректированный коэффициент детерминации:
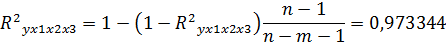
| Регрессионная статистика | |
| Множественный R | 0,990259 |
| R-квадрат | 0,980614 |
| Нормированный R-квадрат | 0,973344 |
| Стандартная ошибка | 21,29465 |
| Наблюдения |
Значимость уравнения регрессии оцениваем через общий F-критерий Фишера:
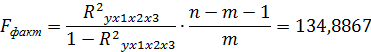
Табличное значение 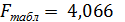 при уровне значимости
при уровне значимости 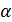 =0,05 и числе степеней свободы 3 и 8. Т.к. 134,8867>4,066, то уравнение статистически значимо. И между
=0,05 и числе степеней свободы 3 и 8. Т.к. 134,8867>4,066, то уравнение статистически значимо. И между 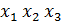 и y существует зависимость.
и y существует зависимость.
Частные F-критерии оценивают целесообразность включения в модель одного фактора после других.
Оценим целесообразность включений 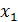 после факторов
после факторов 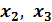 :
:
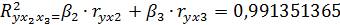
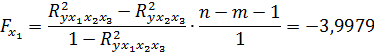
Табличное значение критерия при уровне значимости 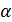 =0,05 и числе степеней свободы 1 и 8 равно
=0,05 и числе степеней свободы 1 и 8 равно 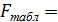 5,318 Т.к.
5,318 Т.к. 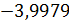 < 5,318 , то не целесообразно включение
< 5,318 , то не целесообразно включение 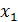 после факторов
после факторов 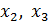 .
.
Оценим целесообразность включений 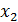 после факторов
после факторов 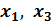 :
:
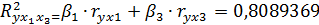
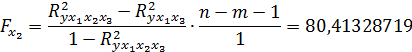
Табличное значение критерия при уровне значимости 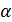 =0,05 и числе степеней свободы 1 и 8 равно
=0,05 и числе степеней свободы 1 и 8 равно 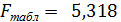 . Т.к.
. Т.к. 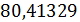 >5,318, то целесообразно включение
>5,318, то целесообразно включение 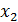 после факторов
после факторов 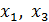 .
.
Оценим целесообразность включений 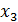 после факторов
после факторов 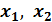 :
:
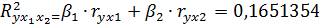
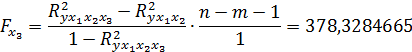
Табличное значение критерия при уровне значимости 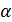 =0,05 и числе степеней свободы 1 и 8 равно
=0,05 и числе степеней свободы 1 и 8 равно 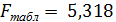 . Т.к.
. Т.к. 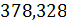 > 5,318, то целесообразно включение
> 5,318, то целесообразно включение 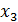 после факторов
после факторов 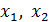 .
.
Частные средние коэффициенты эластичности используются для характеристики относительной силы влияния факторов на 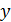 .
.
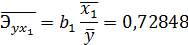
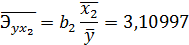
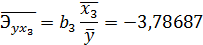
С увеличение 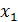 на 1% от своего среднего уровня
на 1% от своего среднего уровня 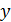 увеличивается на 0,7285% от своего среднего уровня при фиксированных значениях
увеличивается на 0,7285% от своего среднего уровня при фиксированных значениях 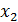 и
и 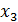 .
.
С увеличение 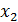 на 1% от своего среднего уровня
на 1% от своего среднего уровня 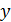 увеличивается на 3,11 % от своего среднего уровня при фиксированных значениях
увеличивается на 3,11 % от своего среднего уровня при фиксированных значениях 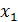 и
и 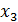 .
.
С увеличение 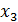 на 1% от своего среднего уровня
на 1% от своего среднего уровня 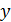 уменьшается на 3,787% от своего среднего уровня при фиксированных значениях
уменьшается на 3,787% от своего среднего уровня при фиксированных значениях 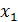 и
и  .
.
Частные коэффициенты эластичности:
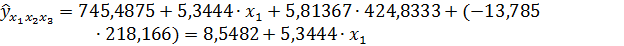
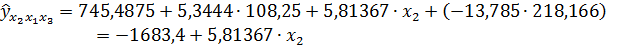
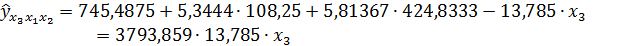
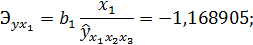
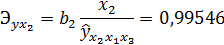
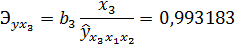
Наибольшее воздействие оказывает 1-й фактор.
Прогноз:
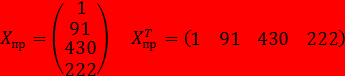
Точечный прогноз:
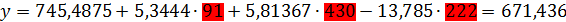
Ошибка прогноза:
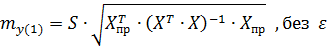
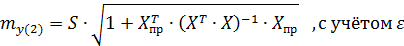
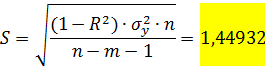
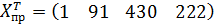
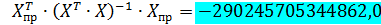
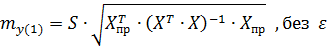
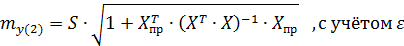
Тогда:
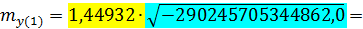 24691483,66
24691483,66
;
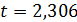 при p=95% и степенях свободы 12-3-1=8
при p=95% и степенях свободы 12-3-1=8
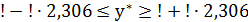
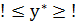

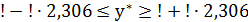
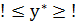
Вывод:
Совокупность неоднородна 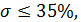 мультиколлинеарность отсутствует
мультиколлинеарность отсутствует 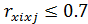 . Множественный коэффициент корреляции близок к 1 (
. Множественный коэффициент корреляции близок к 1 ( 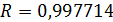 ).
). 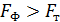 581,289>4,066, то можно сказать, что уравнение статистически значимо. И между
581,289>4,066, то можно сказать, что уравнение статистически значимо. И между 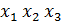 и y существует зависимость. Частные коэффициенты эластичности приблизительно равны средним. Наибольшее воздействие оказывает 1-й фактор.
и y существует зависимость. Частные коэффициенты эластичности приблизительно равны средним. Наибольшее воздействие оказывает 1-й фактор.
|
из
5.00
|
Обсуждение в статье: Самостоятельная работа № 2 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

