Свойства дискретных схем

5.1 Точность

Точность характеризует приемлемость численной схемы для её практического использования. Оценка точности дискретной схемы представляется весьма сложной задачей, поскольку оказывается практически невозможно отделить ошибки, возникшие вследствие свойств схемы, от ошибок, возникших вследствие прочих факторов (таких как ошибки округления, неточность задания граничных и начальных условий и др.).

Когда говорят о точности дискретной схемы, обычно имеют в виду погрешность аппроксимации производных[27]. В частности, если погрешность аппроксимации сопоставима со второй степенью шага расчетной сетки, то говорят, что дискретная схема имеет второй порядок точности. Более подробно этот вопрос рассматривался в § 3.

 

5.2 Согласованность

Дискретная схема называется согласованнойс исходным дифференциальным уравнением, если при измельчении расчетной сетки погрешность аппроксимации (см. § 3) стремится к нулю,

Известны расчетные схемы, у которых для достижения согласованности необходимо выполнение дополнительных условий, [Андерсон и К]. Поскольку проверка согласованности расчетных схем является задачей разработчиков (а не пользователей) программного обеспечения более подробно этот вопрос здесь обсуждаться не будет.

5.3 Устойчивость

Дискретная схема называется устойчивой, если при каждом шаге по маршевой[28] координате случайная ошибка решения не возрастает при переходе от одного шага к другому.

В качестве примера, рассмотрим решение нестационарного уравнения теплопроводности (21) при помощи явной разностной схемы (22а). Соотношение шагов расчетной сетки Δt и Δх выберем таким, чтобы выполнялось условие . Пусть в начальный момент времени температура центрального узла составляет один градус, а температура остальных узлов – нулевая. Граничные условия также примем нулевыми.

Результаты расчета для первых четырех шагов по времени на расчетной сетке, состоящей из девяти узлов, приведены в табл. 5.1. Как следует из этой таблицы, полученные результаты полностью противоречат физическому смыслу – вместо постепенного выравнивания температуры по длине стержня, наблюдается её скачкообразное изменение во всех узлах расчетной сетки, причем амплитуда колебаний постоянно нарастает – решение "идет в разнос".

Таблица 5.1

Номер узла сетки	Номер шага по времени
					-4
				-3
			-2		-16
		-1		-7
			-2		-16
				-3
					-4

На рис. 14а приведен график, демонстрирующий изменение температуры в центральном узле расчетной сетки для случая r=0,513. В этом случае также наблюдаются осцилляции с нарастающей амплитудой, однако, даже после шестидесяти шагов по времени, амплитуда колебаний не превышает одного градуса. Можно доказать, что уменьшение параметра r (за счет уменьшения шага по времени Δt по отношению к шагу Δх) до величины 0,5 полностью ликвидирует осцилляции и позволяет получить физически обоснованное решение. В качестве примера, на рис. 14б приведена зависимость температуры от номера шага по времени для случая r=0,30.

Потеря устойчивости при чрезмерном увеличении шага по маршевой координате характерна для всех явных расчетных схем. Следует отметить, что упомянутое условие устойчивости разностной схемы (22а) r≤0,5 является весьма "жестким". Дело в том, что попытка уменьшения шага по пространственной координате в два раза, вынудит исследователя одновременно уменьшить шаг по времени в четыре раза. В одномерном случае это приведет к увеличению трудоемкости расчета в восемь раз, в двумерном – в шестнадцать раз, а в трехмерном случае трудоемкость расчета возрастет в тридцать два раза!

Простейший практический способ оценки устойчивости разностной схемы заключается в умышленном внесении некоторого возмущения в исходные данные задачи и последующем изучении распространения этого возмущения, подобно тому, как это было сделано в вышеприведенном примере.

К настоящему времени разработан ряд теоретических методов исследования устойчивости линейных дифференциальных уравнений в частных производных, но их изложение выходит за рамки данной работы.

а) r=0,513	б) r=0,30
Рис. 14. Зависимость температуры в центральном узле сетки (i=4) от номера шага по времени

 

5.4 Сходимость

 

Расчетную схему называют сходящейся, если при уменьшении шага сетки решение дискретного аналога стремится к решению исходного дифференциального уравнения, т.е. если выполняется условие вида:

,

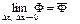(33)

 

где Ф – численное решение дифференциального уравнения;, – точное решение; Δх – шаг по пространственным координатам; Δt – шаг по времени.

Применительно к линейным дифференциальным уравнениям в частных производных доказана теорема Лакса (теорема об эквивалентности):

Необходимым и достаточным условием сходимости разностной схемы для решения корректно поставленной задачи с начальными данными[29] для линейного уравнения в частных производных является выполнение условий согласованности и устойчивости.

Таким образом:

Сходимость = Согласованность + Устойчивость

(34)

 

Доказательство данной теоремы выходит за рамки нашего курса.

Многие авторы предполагают справедливость теоремы Лакса для нелинейных дифференциальных уравнений в частных производных, хотя для таких уравнений эта теорема не доказана [Андерсон и К].

При решении граничных задач итерационными методами (см. п. 4.1), могут возникнуть проблемы, связанные с отсутствием сходимости итераций. Как отмечалось ранее, для повышения устойчивости итерационного процесса, рекомендуется применять нижнюю релаксацию. Следует отметить, что с математической точки зрения, введение нижней релаксации аналогично уменьшению шага по времени при решении маршевых задач.

Практический способ исследования сходимости заключается в решении дискретного аналога дифференциального уравнения на расчетных сетках с различным шагом. Если при анализе результатов расчетов удастся продемонстрировать независимость решения от шага расчетной сетки, то дискретную схему признают сходящейся.

 

[1] Для простоты изложения в данной работе будут рассматриваться только двумерные задачи

[2] Для сравнения имеет смысл указать, что емкость оперативной памяти широко распространенных персональных ЭВМ класса Pentium-IV составляет от 256 до 4000 мегабайт.

[3] Пульсации вязкости обычно полагают малыми и пренебрегают ими.

[4] Для случая несжимаемой жидкости.

[5] В последние годы бурно развивается альтернативный метод упрощения уравнений Навье-Стокса, связанный с разделением пульсаций искомых характеристик течения на крупно- и мелкомасштабные – метод крупных вихрей (Large Eddy Simulation, LES). Уравнения метода LES по форме схожи с уравнениями Рейнольдса (3).

[6] Напряжениями Рейнольдса называются величины

[7] Сплошность (межатомные пустоты не влияют на характер напряженного состояния тела), изотропность (независимость свойств материала от направления), физическая линейность (выполнение закона Гука), геометрическая линейность (малость деформаций по сравнению с размерами тела).

[8] В двумерном случае.

[9] Решением дифференциального уравнения является функция, обращающая это уравнение в тождество.

[10] Для дифференциального уравнения первого порядка. При решении уравнений старших порядков потребуются дополнительные граничные условия для производных, заданные на этой же границе. Попытка задания условий на обеих границах в маршевой задаче может привести к тому, что она окажется несовместной.

[11] См. предыдущее примечание. Важно понимать, что граничная задача требует задания условий на всех границах интервала, а маршевая – только на входной.

[12] Современные цифровые ЭВМ способны оперировать только элементами множества “вещественных” чисел, имеющими ограниченное число значащих цифр, которое определяется “разрядной сеткой” ЭВМ. Можно отметить, что множество вещественных чисел не содержит иррациональных чисел и включает в себя не все рациональные числа. Число элементов множества вещественных чисел, доступного данной ЭВМ, конечно, что влечет за собой принципиальную невозможность описания всего множества действительных чисел, которое бесконечно велико. Вторая причина, вынуждающая нас использовать сеточные функций, заключается в необходимости разумной экономии времени выполнения расчетов.

[13] Процесс построения восполнений (непрерывных функций, совпадающих в узлах сетки со значениями сеточной функции) называется интерполяцией.

[14] Вообще говоря, функция (х) может быть нам не известна. Ставя задачу по оценке её производной, мы тем самым предполагаем, что (х) дифференцируемая.

[15] Для точки х_*, лежащей посередине отрезка (x_k-1,x_k), коэффициент при ²(х_*) в (9) равен нулю и, следовательно, точность оценки производной возрастает.

[16] В случае Δx=const.

[17] Для сравнения: по данным табл. 3.1, вследствие применения пятиточечной аппроксимации, ошибка уменьшилась примерно в 2000 раз!

[18] Описываемый способ интегрирования обыкновенных дифференциальных уравнений называется методом Эйлера.

[19] В случае сетки, имеющей переменные шаги Δx и Δу, формулы будут более громоздкими.

[20] Для определенности будем полагать, что на обоих концах стержня заданы граничные условия Дирихле, а расчетные шаги по пространственной координате Δx и по времени Δt примем постоянными.

[21] Как указывалось выше, время является односторонней координатой, а пространственная координата х – двусторонней (см. § 3). Именно этим обстоятельством объясняется выбор различных аппроксимаций для производных.

[22] Значения температуры при i=0 и i=N известны из граничных условий задачи.

[23] Подобный эффект, например, наблюдается при решении уравнений Прандтля вблизи точки отрыва пограничного слоя [Белоцерковский и др.].

[24] Естественно, вместо критерия сходимости (26) в данном случае должна использоваться величина ε/r.

[25] Современные программно-вычислительные комплексы, как правило, предоставляют пользователю возможность такого выбора.

[26] Использование более точных методов интерполяции возможно, но приведет к более громоздким выкладкам, не изменяя существа дела.

[27] Напомним, что погрешностью аппроксимации называют ошибку, возникающую при замене производной конечно-разностным соотношением.

[28] Теоретическое понятие устойчивости применимо только к маршевым расчетным схемам, однако на практике неустойчивость решения может наблюдаться и у граничных задач.

[29] Т.е. для маршевой задачи.