 |
Главная |
Целочисленное линейное программирование
|
из
5.00
|
1-30.Найти целочисленное решение задач. Дать геометрическую интерпретацию.
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 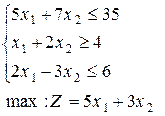
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 
| 20. | 
|
| 21. | 
| 22. | 
|
| 23. | 
| 24. | 
|
| 25. | 
| 26. | 
|
| 27. | 
| 28. | 
|
| 29. | 
| 30. | 
|
| Использование компьютерных технологий для решения задач математического программирования |
4.1 Пакет "The management scientist"
Пакет прикладных программ предназначен для решения задач с использованием методов математического программирования и некоторых задач, содержащих статистические зависимости. Для начала работы в пакете требуется запустить на выполнение файл ms.exe. В появившемся диалоговом окне предлагается выбрать диск, на котором будет происходить работа, на него будут записываться сохраненные задачи и результаты решений. Допустим, нами выбран диск С:, тогда в качестве места работы указывают: С:.
Главное меню программы имеет вид, представленный на рис. 1.
| 1. Линейное программирование 2. Транспортная задача 3. Назначение 4. Целочисленное линейное программирование 5. Кратчайший маршрут 6. Минимальная сеть | 7. PERT/CPM 8. Инвентарь 9. Очереди 10. Анализ решений 11. Прогноз 12. Марковский процесс |
| 13. Выход в doc |
Рисунок 1 – Главное меню пакета
Выбрав требуемый пункт, вводят его номер, например, 2 (это позволит перейти к решению транспортной задачи) и нажимают клавишу ENTER. Для прекращения работы с пакетом следует ввести число 13 или нажать совместно клавиши CTRL и BREAK . Независимо от выбранного пункта появляется стандартное “Меню выбора проблемы” (см. рисунок 2).
| 1. Создать новую проблему 2. Вызвать сохраненную ранее проблему 3. Продолжить работу с текущей проблемой 4. Удалить ранее сохраненную проблему 5. Возврат в меню верхнего уровня |
Рисунок 2 – Меню выбора проблемы
При записи математической моделидействуют следующие правила:
§ имена переменных должны состоять не более, чемиз 14 символов, индексыне используются, например, XI, АВ12, С33;
§ вещественные числа вводятся с использованием точки, отделяющей дробную и целую части 0.7; 3.61;
§ при программировании целевой функции первым указывается ее тип, а затем вводятся коэффициенты при неизвестных:
max 10Х1+3Х2
илиmin 7.4 XI + 6.8 X2;
§ запись вида .53 равносильна 0.53.
Если вводится математическая модель новой задачи или вызывается ранее созданная, то следующий шаг – это работа в меню, представленном на рис. 3.
| Меню работы с проблемой 1. Решить проблему 2. Сохранить проблему 3. Просмотр / Редактирование 4. Вернуться в меню выбора проблемы |
Рисунок 3 – Меню решения задачи
Для получения решения задачи выбирают опцию 1 (рис. 3), для сохранения – 2. При сохранении модуля следует придерживаться следующего правила: имя файла не должно превышать восемь знаков, причем запрещается использовать пробел, запятую, “, /, [ , ], :, <, >, +, =, ;. После того, как задача будет решена, появляется меню, представленное на рисунке 4.
| Меню решения проблемы 1. Вывести ещё раз 2. Вывести решение на принтер 3. Продолжить текущую проблему 4. Вернуться в предыдущее меню |
Рисунок 4 – Меню решения проблемы
Если необходимо скорректировать модель, в “Меню решения задачи” (рис. 3) выбирается соответствующий пункт, передающий управление “Меню редактирования” (рис. 5).
| Меню редактирования 1. Просмотреть проблему 2. Просмотр и редактирование целевой функции 3. Просмотр / Редактирование ограничений 4. Добавка ограничений 5. Удалить ограничение 6. Возврат в меню работы с проблемой |
Рисунок 5 – Меню редактирования задачи
Рассмотрим пример: Найти максимум функции  при ограничениях:
при ограничениях:

В главном меню (рис. 1) выберем опцию “Линейное программирование”, затем, после перехода в меню выбора проблемы (рис. 2) зададим вариант “Создать новую проблему”. Ввод модели осуществляетсяпоэтапно.
Шаг I.
 Введите целевую функцию, используя имена переменных из 14 символов или менее; Введите целевую функцию, используя имена переменных из 14 символов или менее;
| |
Целевая функция: 
|
Шаг II.
Пожалуйста, введите ограничения:
| < для менее илиравно | |
| = для равно | |
| > для более или равно |
После появления слов “ограничение” ввести налагаемыеусловия и нажать ENTER. Когда все условия будут введены,напечатать END.
ограничение 1: 
ограничение 2: 
ограничение 3: 
ограничение 4: 
ограничение 5: 
ограничение 6:end
После завершения ввода математической постановки экстремальной задачи пакет автоматически переходит в меню работы с проблемой (рис. 3). Перед дальнейшим использованием модель желательно сохранить, выбрав соответствующую опцию меню. Дадим ей имя LP1. Решение задачи будет распечатано в виде
Целевая функция Значение = 32.8
| Переменные -------------------------- | Значения ––––––––––––––––– | Измененные цены –––––––––––––––––––– |
| XI | 1.6 | 0.0 |
| Х2 | 5.6 | 0.0 |
| Ограничения --------------------- | Недостаток/Избыток ------------------------------- | Чувствительность ------------------------–- |
| 9.2 | 0.0 | |
| 0.0 | 0.7 | |
| 0.0 | 0.5 | |
| 4.0 | 0.0 | |
| 38.2 | 0.0 |
Величины, указанные в колонке “Недостаток/ Избыток”, означают резерв ресурса, отраженного в соответствующем ограничении. Колонка “Чувствительность” показывает, на сколько улучшится оптимальное значение при увеличении на единицу значения правой стороны неравенства. Так, для второго ограничения повышение ресурса на единицу приведет к увеличению значения целевой функции на 0.7. Аналогично для других ограничений.
Следующая таблица характеризует:
§ нижние и верхние пределы коэффициентов, в пределах которых может меняться один из коэффициентов, и при этом решение будут обеспечивать те же значения;
§ диапазоны правой части неравенств, для которой чувствительность остается постоянной.
|
из
5.00
|
Обсуждение в статье: Целочисленное линейное программирование |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

