 |
Главная |
Метод золотого сечения
|
из
5.00
|
Поиск экстремума. Вводные замечания.
Под задачей оптимизации будем понимать нахождение экстремума (минимума или максимума) функции одного или нескольких вещественных переменных. К решению оптимизационных задач сводятся задачи поиска корней нелинейных уравнений и систем, аппроксимации функций и др.
Пусть дана вещественная функция 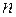 вещественных переменных
вещественных переменных 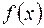 ,
, 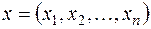 , определенная в замкнутой области
, определенная в замкнутой области  . Требуется найти
. Требуется найти
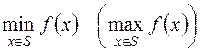
| (13.1) |
и точку  , в которой он достигается.
, в которой он достигается.
Заметим, что поиск максимума функции 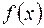 эквивалентен поиску минимума функции
эквивалентен поиску минимума функции 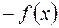 . Поэтому далее будем рассматривать задачу минимизации.
. Поэтому далее будем рассматривать задачу минимизации.
Множество  выражает ограничения задачи. Например, во многих физических задачах, требуется, чтобы переменные были неотрицательны:
выражает ограничения задачи. Например, во многих физических задачах, требуется, чтобы переменные были неотрицательны: 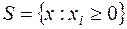 . Если
. Если  совпадает с
совпадает с  , то говорят о задаче безусловной оптимизации, в противном случае говорят об условной оптимизации.
, то говорят о задаче безусловной оптимизации, в противном случае говорят об условной оптимизации.
Будем говорить, что 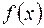 имеет в точке
имеет в точке  глобальный минимум, если
глобальный минимум, если  для любого
для любого 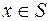 . Аналогично,
. Аналогично, 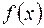 имеет в точке
имеет в точке  локальный минимум, если
локальный минимум, если  для любого
для любого 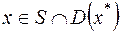 , где
, где 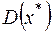 – окрестность точки
– окрестность точки  .
.
Если локальный минимум (экстремум) достигается во внутренней точке  области
области  и функция
и функция 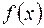 дифференцируема в этой точке, то
дифференцируема в этой точке, то  является критической точкой, т.е. выполняются условия:
является критической точкой, т.е. выполняются условия:
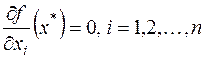
| (13.2) |
Обратное, вообще говоря, неверно: критическая точка может не быть экстремумом (например, точка перегиба).
Мы ограничимся поиском локальных минимумов в задаче безусловной оптимизации. Отметим, что таких минимумов (как и максимумов) на заданном интервале может быть несколько, поэтому нам необходимо локализовать экстремум, т.е. определять отрезок с единственной экстремальной точкой функции 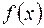 .
.
13.1. Одномерная оптимизация.
Метод Ньютона
В основе метода Ньютона лежит приближение функции 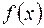 в окрестности экстремума квадратичной функцией
в окрестности экстремума квадратичной функцией  . В свою очередь, экстремум квадратичной функции
. В свою очередь, экстремум квадратичной функции  находится явно (
находится явно ( 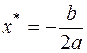 - абсцисса экстремума) и используется в качестве следующего начального приближения.
- абсцисса экстремума) и используется в качестве следующего начального приближения.
Пусть некоторая точка 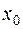 – приближение абсциссы экстремума. Запишем разложение функции
– приближение абсциссы экстремума. Запишем разложение функции  в ряд Тейлора в окрестности
в ряд Тейлора в окрестности 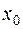 (для квадратичной функции отличны от нуля только первые две производные):
(для квадратичной функции отличны от нуля только первые две производные):

| (13.3) |
Правая часть выражения (13.3) представляет собой квадратичную функцию относительно  (
( 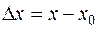 ), экстремум которой достигается в точке
), экстремум которой достигается в точке

| (13.4) |
Раскрывая  , в качестве следующего приближения можем взять
, в качестве следующего приближения можем взять

Получаем итерационный процесс:
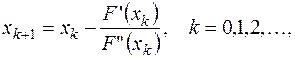
| (13.5) |
дающий алгоритм метода Ньютона.
Отметим, что при выборе начального приближения достаточно близко к точке экстремума метод Ньютона гарантированно сходится. Однако метод Ньютона может сходиться как к локальному минимуму, так и к локальному максимуму, поэтому в полученной точке экстремума 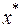 , если не использовать локализацию, требуется дополнительно вычислить
, если не использовать локализацию, требуется дополнительно вычислить  , причем, если
, причем, если  , то мы имеет дело с локальным минимумом, если же
, то мы имеет дело с локальным минимумом, если же  – с локальным максимумом, если
– с локальным максимумом, если  – метод Ньютона завершится делением на 0.
– метод Ньютона завершится делением на 0.
Пример 1.Найти точку минимума функции 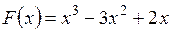 . Сделать три итерации.
. Сделать три итерации.
Решение.Для применения формулы (13.5) вычислим производные:  ,
, 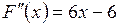 . Подставляя в (13.5), получим:
. Подставляя в (13.5), получим:  . Выберем в качестве начального приближения
. Выберем в качестве начального приближения  . Подставляя в расчётную формулу, последовательно найдём
. Подставляя в расчётную формулу, последовательно найдём  . Точное значение
. Точное значение  . Если в качестве начального приближения выбрать значение
. Если в качестве начального приближения выбрать значение  , то остановится, не начавшись, т.к. в этом случае
, то остановится, не начавшись, т.к. в этом случае 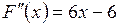 равна нулю (значение
равна нулю (значение  является точкой перегиба исходной функции).
является точкой перегиба исходной функции).
Метод золотого сечения.
Метод золотого сечения – метод разбиения отрезка: отношение длины большей части к длине всего отрезка равно отношению длины меньшей части отрезка к длине его большей части, т.е. выполняется пропорция золотого сечения (рис. 2.).
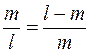
| (13.6) |
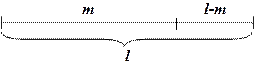
Рис. 2.
Разрешая пропорцию (13.6) относительно 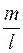 и учитывая тот факт, что длина отрезка не может быть отрицательной, получаем
и учитывая тот факт, что длина отрезка не может быть отрицательной, получаем

Число  называется золотым сечением и является фундаментальным числом, возникающим во многих областях науки и техники.
называется золотым сечением и является фундаментальным числом, возникающим во многих областях науки и техники.
|
из
5.00
|
Обсуждение в статье: Метод золотого сечения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

