 |
Главная |
Коэффициенты эластичности в нелинейных регрессиях
|
из
5.00
|
Степенная функция используется в эконометрических исследованиях очень широко. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, то есть он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
ПРИМЕР
Кривая Энгеля была построена для расходов на питание в США за период с 1959 по 1983 г. с использованием тех же данных, что и в лекции «Парная линейная регрессия», однако вместо линейной функции в данном случае использовалась нелинейная, приведенная к линейному виду путем взятия логарифмов. Преобразованное выражение имело вид :
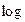 y = 1,20 + 0,55 log x
y = 1,20 + 0,55 log x
Выполнив обратные преобразования, получим
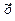 = е 1,20х 0,55 = 3,32 х 0,55
= е 1,20х 0,55 = 3,32 х 0,55
Если уравнение (4.6.) представляет собой правильную формулу зависимости ( в действительности, это, безусловно, сильно упрощено), то полученный результат предполагает, что эластичность спроса на продукты питания по доходу составляет 0,55, что означает, что увеличение личного располагаемого дохода на 1% приведет к увеличению расходов на питание на 0,55%. Коэффициент 3,32 не имеет простого толкования. Он помогает прогнозировать значения у при заданных значениях х, приводя их к единому масштабу.
О правомерности подобного истолкования параметра b можно судить, если рассмотреть формулу расчета коэффициента эластичности
Э= 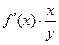
 4.13.
4.13.
где 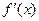 - первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Для степенной функции она составит
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Для степенной функции она составит 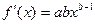 . Соответственно коэффициент эластичности окажется равным
. Соответственно коэффициент эластичности окажется равным
Э = 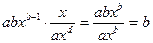 4.14.
4.14.
Коэффициент эластичности можно определить и для других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b. В других функциях коэффициент эластичности зависит от значения фактора х. Так, для линейной регрессии у=а+bх коэффициент эластичности определяется по формуле
Э= 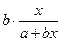 4.15.
4.15.
так как 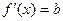 .
.
В силу того, что для линейной функции коэффициент эластичности не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле
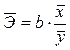 4.16.
4.16.
Для параболы второго порядка у=а+bx+cx2 первая производная функции 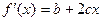 , а коэффициент эластичности также зависит от величины х
, а коэффициент эластичности также зависит от величины х
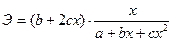 4.17.
4.17.
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в %. Например, не имеет смысла определять в % такие признаки, как возраст, число комнат, тарифный разряд рабочего и др. В такой ситуации степенная функция не может быть экономически интерпретирована, поэтому даже если она оказывается наилучшей по формальным математическим соображениям (минимальная остаточная дисперсия), значительно больший интерес для интерпретации может иметь линейная регрессия с меньшим коэффициентом корреляции.
5. Корреляция для нелинейной регрессии.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем тесноты связи, а именно – индексом корреляции R
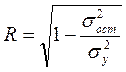 4.18.
4.18.
где 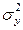 -общая дисперсия результативного признака;
-общая дисперсия результативного признака;
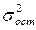 - остаточная дисперсия.
- остаточная дисперсия.
Учитывая связь дисперсии с объемом вариации, можно легко доказать, что индекс корреляции через объемы вариации определяется следующим образом:
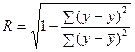 4.19.
4.19.
Нам уже известно, что величина данного показателя находится в пределах от нуля до единицы. Чем он ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняющей переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого совпадет с индексом корреляции. (Доказательство дано в учебнике Елисеевой И.И. «Эконометрика»)
Обратимся к равносторонней гиперболе 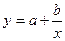 . Заменив
. Заменив 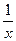 на z, имеем регрессию вида
на z, имеем регрессию вида 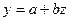 , для которой может быть определен линейный коэффициент корреляции
, для которой может быть определен линейный коэффициент корреляции 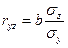 . По своей величине он будет равен коэффициенту корреляции между у и х , то есть ryч.
. По своей величине он будет равен коэффициенту корреляции между у и х , то есть ryч.
Иначе обстоит дело, когда преобразование уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции. Так, для степенной функции 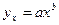 после перехода к логарифмически линейному уравнению loqy=loqa+bloqx может быть найден линейный коэффициент корреляции не для фактических значений переменных у и х, а для их логарифмов (то есть rloqy.loqx). Квадрат линейного коэффициента корреляции будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов. Между тем при расчете индекса корреляции используются суммы квадратов отклонений именно у, а не их логарифмов.
после перехода к логарифмически линейному уравнению loqy=loqa+bloqx может быть найден линейный коэффициент корреляции не для фактических значений переменных у и х, а для их логарифмов (то есть rloqy.loqx). Квадрат линейного коэффициента корреляции будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов. Между тем при расчете индекса корреляции используются суммы квадратов отклонений именно у, а не их логарифмов.
Квадрат индекса корреляции (i2) называют индекс детерминации, он имеет тот же смысл, что и линейный коэффициент детерминации, то есть представляет собой отношение факторной и общей суммы квадратов отклонений.
Индекс детерминации используется для проверки существенности уравнения нелинейной регрессии в целом по F-критерию Фишера
F = 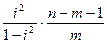 4.20.
4.20.
где п – число наблюдений;
т – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной дисперсии, а (n – m – 1) – число степеней свободы для остаточной суммы квадратов. Для степенной функции т=1 и формула F-критерия примет тот же вид, что и при линейной парной зависимости
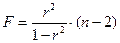 4.21.
4.21.
Для параболы второй степени m=2 и
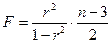 4.22.
4.22.
Расчет критерия Фишера можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции (лекция 3).
Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем меньше значение линейного коэффициента детерминации по сравнению с индексом детерминации. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина i2-r2≤0.1 , то предположение о линейной форме связи считается оправданным. Иными словами, если нет уверенности в правильности выбора нелинейной функции, то в целях лучшей интерпретации связи она может быть заменена уравнением прямой.
Возможность построения нелинейных моделей значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя – возникает проблема выбора. Выбор модели с максимальным коэффициентом детерминации не всегда возможен. В частности, нельзя сравнивать эти показатели для линейного и логарифмического вариантов модели. В большинстве случаев лучшей следует признать модель, которая при достоверных параметрах имеет меньший объем остаточной вариации, легче интерпретируется и требует меньшего объема наблюдений.
Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.
Факторами производственной функции могут являться следующие переменные:
1) объём выпущенной продукции (в стоимостном или натуральном выражении);
2) объём основного капитала или основных фондов;
3) объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней);
4) затраты электроэнергии;
5) количество станков, потребляемое в производстве и др.
Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных.
Основными разновидностями однофакторных производственных функций являются:
1) линейная однофакторная производственная функция вида:
y=β0+β1x,
например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями:
а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β0(β0›0);
б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β1 (β1›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике;
2) параболическая однофакторная производственная функция вида:
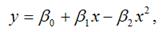
при условиях β0›0, β1›0, β2›0.
Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;
3) степенная однофакторная производственная функция вида:
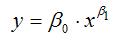
при условиях β0›0, β1›0.
Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;
4) показательная однофакторная производственная функция вида:
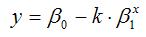
при условиях 0‹β1‹0.
Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0.
5) гиперболическая однофакторная производственная функция вида:
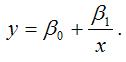
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.
Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.
Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами.
Изоквантойназывается сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства.
Многофакторные производственные функции используются для изучения зависимости объёма производства от n-го количества факторов производства.
Общий вид многофакторной производственной функции:
y=f(xi),
где
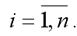
|
из
5.00
|
Обсуждение в статье: Коэффициенты эластичности в нелинейных регрессиях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

