 |
Главная |
Вращательное броуновское движение
|
из
5.00
|
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра общей физики
БРОУНОВСКОЕ
ДВИЖЕНИЕ.
ТЕМПЕРАТУРА
Учебно-методическое пособие для студентов
Специальности 1 - 31 04 01 «Физика»
МИНСК
БРОУНОВСКОЕ ДВИЖЕНИЕ
Сущность и причины
Броуновского движения
Пусть небольшое макроскопическое тело массы 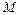 находится в жидкой или газообразной среде. Предположим, что сила тяжести отсутствует либо скомпенсирована какими-либо силами, например, архимедовой подъёмной силой. Под воздействием ударов молекул среды центр масс тела совершает беспорядочные тепловые движения, скорость которых:
находится в жидкой или газообразной среде. Предположим, что сила тяжести отсутствует либо скомпенсирована какими-либо силами, например, архимедовой подъёмной силой. Под воздействием ударов молекул среды центр масс тела совершает беспорядочные тепловые движения, скорость которых:
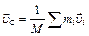 ,
,
где 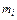 – масса, а
– масса, а 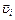 – скорость
– скорость 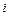 -ой молекулы тела.
-ой молекулы тела.
Возведя в квадрат, получим
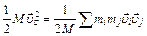
Усредним по времени. Ввиду хаотичности теплового движения молекул тела их скорости не скоррелированы, поэтому 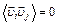 при
при 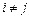 .
.
Тогда 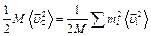
Для каждой молекулы тела 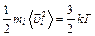 ,
,
следовательно, 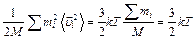
В результате: 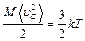 .
.
Таким образом, при тепловом равновесии на поступательное движение центра масс макроскопического тела в среднем приходится та же энергия 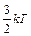 , что и на поступательное движение одной молекулы. В этом отношении тело можно рассматривать как гигантскую молекулу.
, что и на поступательное движение одной молекулы. В этом отношении тело можно рассматривать как гигантскую молекулу.
Аналогично можно показать, что 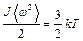 .
.
Если маленькие твёрдые частицы размером порядка 10-6 м поместить в каплю жидкости и наблюдать их под микроскопом, то оказывается, что частицы не находятся в покое, а постоянно движутся в разных направлениях.
Это явление получило название броуновского движения в честь английского ботаника Броуна, который впервые наблюдал его в 1827 г.
Энергия 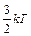 , приходящаяся на три поступательные степени свободы частицы, приводит к движению её центра масс, которое и наблюдается под микроскопом в виде дрожания.
, приходящаяся на три поступательные степени свободы частицы, приводит к движению её центра масс, которое и наблюдается под микроскопом в виде дрожания.
В 1905 г. Эйнштейн объяснил броуновское движение случайными флуктуациями, возникающими в состоянии равновесия. Движение твёрдых частиц в жидкости подвержено воздействию флуктуаций силы, появляющейся в результате многих случайных столкновений молекул жидкости с этими частицами. Так как броуновские частицы имеют небольшой размер, то число молекул, взаимодействующих с ними в единицу времени, также мало, и соответственно флуктуации велики. Результирующее случайное движение частицы поэтому легко наблюдать. Броуновское движение наглядно подтверждает представления молекулярно-кинетической теории о хаотическом тепловом движении атомов и молекул.
Случайное блуждание
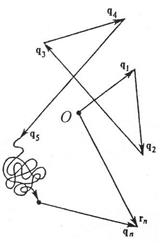
| Рассмотрим положение броуновской частицы через некоторые фиксированные промежутки времени 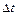 (см. рис.):
точка O – начало координат, (см. рис.):
точка O – начало координат,
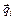 – вектор перемещения между двумя наблюдениями.
Следует отметить, что перемещение частицы в промежутках времени между моментами наблюдения также происходит по сложной изломанной линии.
По истечении – вектор перемещения между двумя наблюдениями.
Следует отметить, что перемещение частицы в промежутках времени между моментами наблюдения также происходит по сложной изломанной линии.
По истечении 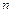 наблюдений радиус-вектор частицы: наблюдений радиус-вектор частицы: 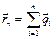 .
Вычислим средний квадрат удаления частицы от начала после .
Вычислим средний квадрат удаления частицы от начала после 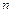 шагов в большой серии опытов: шагов в большой серии опытов:
|
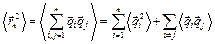 ,
,
где 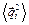 – средний квадрат смещения частицы на
– средний квадрат смещения частицы на 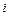 -ом шаге (в большой серии опытов он для всех шагов одинаков и равен какой-то положительной величине, которую обозначим как
-ом шаге (в большой серии опытов он для всех шагов одинаков и равен какой-то положительной величине, которую обозначим как 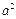 ).
).
Кроме того, 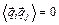 при
при 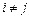 (т.к. перемещения при
(т.к. перемещения при 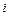 -ом и
-ом и 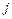 -ом шаге являются независимыми величинами).
-ом шаге являются независимыми величинами).
Поэтому 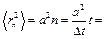
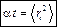 ,
,
где 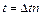 – время, в течение которого средний квадрат удаления частицы стал равным
– время, в течение которого средний квадрат удаления частицы стал равным 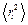 .
.
Таким образом, несмотря на то, что направления, в которых частица перемещается при каждом шаге, равновероятны, в среднем частица будет удаляться от её начального положения, поскольку 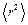 ~
~ 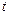 .
.
Расчёт движения
Броуновской частицы
Будем считать, что броуновская частица имеет форму шарика радиуса 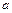 . При равномерном движении шарика в жидкости со скоростью
. При равномерном движении шарика в жидкости со скоростью 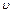 на него действует сила сопротивления, определяемая формулой Стокса:
на него действует сила сопротивления, определяемая формулой Стокса:
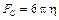
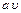 , где
, где 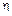 – вязкость жидкости.
– вязкость жидкости.
Т.е. 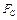 ~
~ 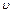 или записывают
или записывают 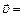
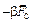 , где
, где 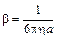 – подвижность частицы.
– подвижность частицы.
Уравнение движения броуновской частицы в направлении оси 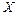 имеет вид
имеет вид
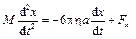 , (1)
, (1)
где 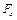 – проекция случайной силы, возникающей за счёт беспорядочных ударов молекул о частицу.
– проекция случайной силы, возникающей за счёт беспорядочных ударов молекул о частицу.
Слагаемое 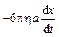 также обусловлено толчками молекул (в сред-
также обусловлено толчками молекул (в сред-
нем толчки, действующие против движения, сильнее толчков, действующих в направлении движения).
Умножим (1) на 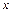 и учтём тождества:
и учтём тождества:
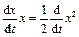 ;
;
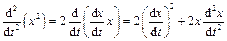
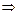
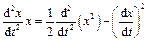
Тогда 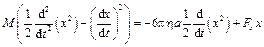 .
.
Усредним по ансамблю броуновских частиц
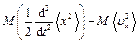
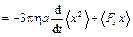 (2)
(2)
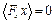 ввиду случайного характера силы
ввиду случайного характера силы 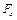 и координаты частицы
и координаты частицы 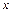 и их независимости друг от друга.
и их независимости друг от друга.
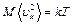 в соответствии с теоремой о равнораспределении энергии по степеням свободы.
в соответствии с теоремой о равнораспределении энергии по степеням свободы.
Из предыдущего пункта:
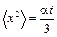 (поскольку
(поскольку 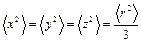 ).
).
Подставив в (2), получаем: 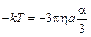 , т.е.
, т.е. 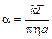 .
.
Значит, 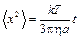 или
или
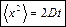 – формула Эйнштейна,
– формула Эйнштейна,
где 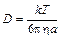 – коэффициент диффузии для сферических частиц.
– коэффициент диффузии для сферических частиц.
Формулу Эйнштейна можно записать в виде
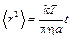 – средний квадрат смещения частицы пропорционален времени.
– средний квадрат смещения частицы пропорционален времени.
Коэффициент пропорциональности не зависит от массы частицы.
Опыты Перрена.
Вращательное броуновское движение.
Опыт Капплера
Формула Эйнштейна была экспериментально подтверждена французским физиком Жаном Перреном в ряде работ, начатых в 1908 г.
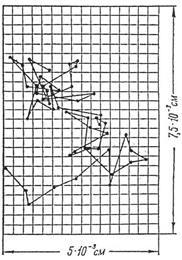
Перрен отмечал через равные промежутки времени (τ=30 c) положения в поле зрения микроскопа броуновской частицы, взвешенной в воде (см. рис.).
Серия опытов позволяет вычислить значение среднего квадрата смещения 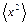 и по формуле и по формуле 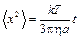 найти постоянную Больцмана найти постоянную Больцмана 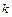 и число Авогадро и число Авогадро  . Перрен получил для них значения, согласующиеся с другими методами. . Перрен получил для них значения, согласующиеся с другими методами.
|
|
Вращательное броуновское движение – беспорядочное вращение броуновской частицы под влиянием ударов молекул среды.
Средний квадрат углового смещения частицы:
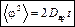 ,
,
где 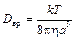 – коэффициент диффузии вращательного броуновского движения для сферической частицы.
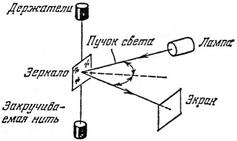
Модельный опыт по наблюдению вращательного броуновского движения поставлен Капплером в 1932 г. (см. рис.) и состоит в следующем. – коэффициент диффузии вращательного броуновского движения для сферической частицы.
Модельный опыт по наблюдению вращательного броуновского движения поставлен Капплером в 1932 г. (см. рис.) и состоит в следующем.
|
|
На очень тонкой кварцевой нити подвешивается маленькое зеркальце.
Под действием ударов молекул окружающего газа зеркальце совершает беспорядочные крутильные колебания около положения равновесия. Это и есть вращательное броуновское движение. Для его наблюдения на зеркальце направляется световой луч. По положению светового зайчика на шкале можно определить угловое положение зеркальца.
Малые крутильные колебания являются гармоническими, поэтому
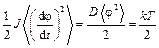 ,
,
где использована теорема о равнораспределении энергии по степеням свободы,
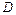 – модуль кручения нити,
– модуль кручения нити,
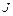 – момент инерции зеркальца.
– момент инерции зеркальца.
Тогда 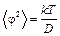 .
.
Полученные с помощью этой формулы результаты для 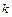 хорошо согласуются с найденными из опытов по проверке распределения Больцмана и исследованию поступательного броуновского движения.
хорошо согласуются с найденными из опытов по проверке распределения Больцмана и исследованию поступательного броуновского движения.
ТЕМПЕРАТУРА
|
из
5.00
|
Обсуждение в статье: Вращательное броуновское движение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

