Импульс (количество движения)

материальной точки р = mν,

где m – масса материальной точки.

 

 

Основное уравнение динамики мате-

Риальной точки (второй закон

Ньютона)

F = ma.

Закон сохранения импульса для

изолированной системы Σm_iν_i = const.

 

Радиус-вектор центра масс r_c = Σm_ir_i/Σm_i.

 

Скорости частиц после столкновения:

упругого центрального

u₁ = - ν₂ + 2 ,

u₂ = - ν₂ + 2 ;

неупругого

u₁ = u₂ = ,

где ν₁ и ν₂ – скорости частиц до

столкновения,

m₁ и m₂ – массы частиц.

 

Сила сухого трения F_тр = f F_n,

где f – коэффициент трения,

F_n – сила нормального давления.

 

Сила упругости F_уп = kΔl,

где k – коэффициент упругости

(жесткость),

Δl – деформация.

 

Сила гравитационного взаимо-

Действия

,

где m₁ и m₂ – массы частиц,

G – гравитационная постоянная,

r – расстояние между частицами.

 

Работа силы .

Мощность .

Потенциальная энергия:

упругодеформированного тела;

 

 

гравитационного взаимодейст-

вия двух частиц ;

тела в однородном гравита-

ционном поле ,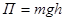

где g – напряженность гравитационного

поля (ускорение свободного

падения),

h – расстояние от нулевого уровня.

 

Напряженность гравитационного

поля Земли ,

где М_з – масса Земли,

R_з – радиус Земли,

h – расстояние от поверхности

Земли.

 

Потенциал гравитационного поля

Земли .

 

Кинетическая энергия материальной

точки

Закон сохранения механической

энергии

Момент инерции материальной

точки ,

где r – расстояние до оси вращения.

 

Момент инерции тел массой m отно-

Сительно оси, проходящей через

центр масс:

тонкостенного цилиндра (коль-

ца) радиуса R, если ось вращения

совпадает с осью цилиндра ;

 

сплошного цилиндра (диска) ра-

диуса R, если ось вращения

совпадает с осью цилиндра ;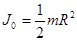

 

шара радиуса R ,

 

тонкого стержня длиной l, если

ось вращения перпендикулярна

стержню .

 

Момент инерции тела массой m отно-

Сительно произвольной оси (теорема

Штейнера) ,

где J₀ – момент инерции относительно

параллельной оси, проходящей

через центр масс,

d – расстояние между осями.

 

Момент силы ,

где r – радиус-вектор точки приложения

силы.

 

Момент импульса .

 

Основное уравнение динамики вра-

щательного движения

 

Закон сохранения момента импульса

для изолированной системы

Работа при вращательном движении

Кинетическая энергия вращающе-

гося тела

Релятивистское сокращение длины

где l₀ – длина покоящегося тела,

с – скорость света в вакууме.

 

Релятивистское замедление времени

где t₀ – собственное время.

 

Релятивистская масса

где m₀ – масса покоя.

 

Энергия покоя частицы

Полная энергия релятивистской

частицы

Релятивистский импульс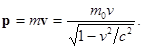

Кинетическая энергия релятивистс-

кой частицы

Релятивистское соотношение между

полной энергией и импульсом