 |
Главная |
Метод зеркальных изображений
|
из
5.00
|
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Решение многих задач электростатики, т.е. определение электростатического поля системы покоящихся зарядов, не требующее интегрирования дифференциальных уравнений Лапласа и Пуассона, возможно в тех случаях, когда поле обладает определенной симметрией. При отсутствии таковой обращаются, если это возможно, к приемам, приближающим систему к симметричной. Одним из таких приемов является метод зеркальных изображений, применяемый тогда, когда поле ограничено проводящими поверхностями правильной геометрической формы - например, плоской либо цилиндрической, - а также поверхностями имеющими геометрически правильную границу раздела между диэлектрическими средами.
Метод практически в разной мере пригоден и для расчетов электрических полей постоянного тока аналогичной структуры, если поменять величины зарядов на токи, а характеристики диэлектрических сред - на характеристики проводников. С некоторыми ограничениями методом пользуются также при расчете магнитных полей постоянные токов.
Эти приемы нашли наибольшее применение при изучении и расчетах электростатических и электрических полей плоскопараллельной структуры, которые изменяются лишь в определенной плоскости и являются функциями только двух координат. В направлении, перпендикулярном этой плоскости, рассматриваемое поле не изменяется.

В дальнейшем изучаются только плоскопараллельные поля, в этом случае плоские границы между средами превращаются в прямые линии, а цилиндрические поверхности - в окружности.
Основой метода зеркальных изображений является поле двух параллельных осей, заряженных равными по величине и обратными по знакам электрическими зарядами  и
и  (рис. 1). Эта модель позволяет описать поле между проводом и землей (эквипотенциальные поверхности 1 и 2), поле двухпроводной линии (2 и 3), поле параллельных цилиндров различных диаметров (3 – 4), поле анаксиального кабеля (2 – 4 ):
(рис. 1). Эта модель позволяет описать поле между проводом и землей (эквипотенциальные поверхности 1 и 2), поле двухпроводной линии (2 и 3), поле параллельных цилиндров различных диаметров (3 – 4), поле анаксиального кабеля (2 – 4 ):
Метод зеркальных изображений
Сущность метода состоит в том, что вместо поля электрических зарядов, расположенных в однородной среде вблизи границы с другой, проводящей или диэлектрической средой, рассматривается вспомогательное поле в однородной среде. В его создании участвуют как заданные, так и дополнительные заряды, величины и местоположение которых выбираются таким образом, чтобы были удовлетворены граничные условия исходного поля. Если граница раздела между двумя средами плоская, дополнительные (их иногда называют «фиктивными») заряды помещаются там, где находятся зеркальные, в геометрическом смысле, отображения заданных зарядов.
Обоснованием метода зеркальных изображений и правильности полученного в результате его применения решения служит теорема единственности, согласно которой электрические поля в областях, ограниченных геометрически совпадающими поверхностями, тождественны, если одинаковы граничные условия.
Рассмотрим в качестве примера электрическое поле равномерно заряженного положительным зарядом прямолинейного провода, расположенного параллельно плоской поверхности проводящей среды. Это соответствует прикладной задаче о проводе, подвешенном над поверхностью земли с достаточно большой электропроводностью.
Все линии напряженности поля, начинающиеся на положительно заряженном проводе, заканчиваются на поверхности проводящей среды, где появляется индуктированный отрицательный заряд (рис. 2). Поле определяется как зарядами провода, тан и всеми зарядами, распределенными по поверхности проводящей среды. Распределение индуктированного заряда вдоль проводящей поверхности из условий задачи неизвестно и его необходимо определить, что значительно усложняет решение. Между тем, применение метода зеркальных изображений быстро приводит к решению.
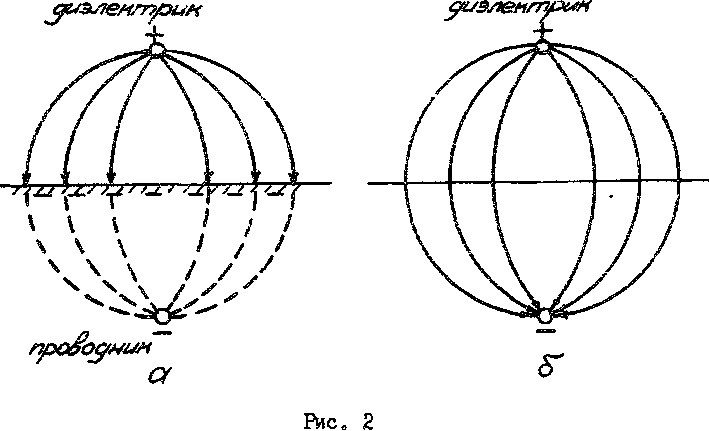
Устраним мысленно проводящую среду и заменим систему провод-земля расположенной в однородной диэлектрической среде системой провод-провод (см. рис. 2,б), причем вспомогательный провод является зеркальным отражением реального провода относительно поверхности раздела и несет заряд той же величины, что и реальный провод, но противоположного знака. Действительный провод и его зеркальное изображение составляют двухпроводную линию, а плоскость, расположенная посредине между ними, является поверхностью равного потенциала. В действительных условиях поверхность проводящей среды геометрически совпадает с этой плоскостью и также является поверхностью равного потенциала.
Отсюда следует, что если заменить проводящую среду зеркальным изображением провода (с изменением знака заряда), то в области над проводящей поверхностью поле останется таким же, как в исходной задаче.
Более сложным и не столь наглядным оказывается применение метода зеркальных изображений при цилиндрической поверхности проводящей среды. Если положительно заряженный прямолинейный провод расположен внутри проводящего цилиндра параллельно его оси (рис. 3,а), силовые линии поля начинаются на положительно заряженном проводе и заканчиваются на поверхности проводящего цилиндра. Зеркально отобразить заряженную ось относительно поверхности цилиндра – это найти такое положение вспомогательной отрицательно заряженной оси (рис. 3,б), при котором в поле двух осей, заданной и вспомогательной» при отсутствии проводящей цилиндрической поверхности одна из эквипотенциальных поверхностей геометрически совпадает с поверхностью удаленного цилиндра. Поле внутри этой эквипотенциали совпадает с искомым полем, а силовые линии расчетной модели начинаются на заданной оси и оканчиваются на вспомогательной.

Метод зеркальных изображений применим также в случае двух или нескольких заряженных достаточно тонких проводов, расположенных параллельно друг другу вблизи проводящей поверхности. Конкретное применение метода при этом усложняется.
Если имеется плоская граница раздела между двумя диэлектриками с различными проницаемостями, можно использовать модификацию метода зеркальных изображений.
На рис. 4 верхнее полупространство представляет собой среду с диэлектрической проницаемостью 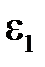 , нижнее – с
, нижнее – с 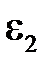 . Между ними располагается плоская граница раздела. В верхнем полупространстве параллельно границе раздела сред находится заряженная ось с линейной плотностью зарядов
. Между ними располагается плоская граница раздела. В верхнем полупространстве параллельно границе раздела сред находится заряженная ось с линейной плотностью зарядов  . Вследствие поляризации диэлектриков на границе раздела появляются связанные заряды, которые влияют на поле в обеих средах. Влияние связанных зарядов на поле учитывают, вводя два дополнительных фиктивных заряда
. Вследствие поляризации диэлектриков на границе раздела появляются связанные заряды, которые влияют на поле в обеих средах. Влияние связанных зарядов на поле учитывают, вводя два дополнительных фиктивных заряда  и
и 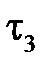 . При этом необходимо удовлетворить граничным условиям, что и достигается подбором соответствующих значений этих зарядов.
. При этом необходимо удовлетворить граничным условиям, что и достигается подбором соответствующих значений этих зарядов.
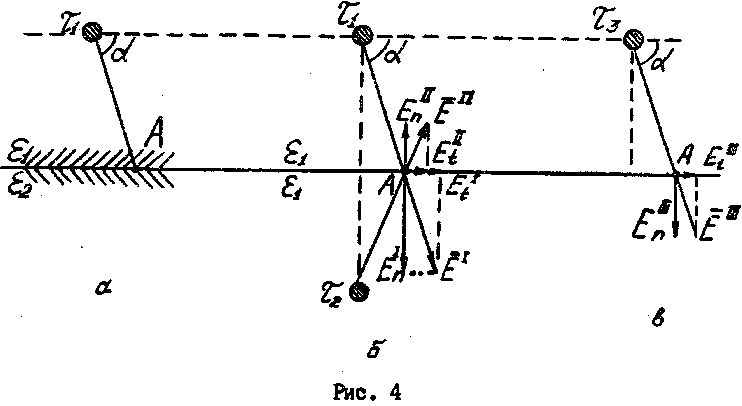
Поле в любой точке верхнего полупространства рассчитывают от двух зарядов: заданного  и фиктивного
и фиктивного  , расположенного в зеркально отраженной точке. При этом и верхнее, и нижнее полупространства заполнены средой с проницаемостью (см. рис. 4,б). Поле в любой точке нижнего полупространства рассчитывают как поле от фиктивного заряда
, расположенного в зеркально отраженной точке. При этом и верхнее, и нижнее полупространства заполнены средой с проницаемостью (см. рис. 4,б). Поле в любой точке нижнего полупространства рассчитывают как поле от фиктивного заряда 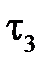 , расположенного в той же точке, где находится заданный заряд
, расположенного в той же точке, где находится заданный заряд  . В этом случае и верхнее, и нижнее полупространства заполнены диэлектриком с проницаемостью
. В этом случае и верхнее, и нижнее полупространства заполнены диэлектриком с проницаемостью  (см. рис. 4,в).
(см. рис. 4,в).
Для определения величины и знака фиктивных зарядов  и
и  воспользуемся граничными условиями в электростатике:
воспользуемся граничными условиями в электростатике:
 и
и  и рис. 4,в, и 4,б.
и рис. 4,в, и 4,б.
Из условия равенства тангенциальных, составляющих вектора на границе раздела, приняв за положительное направление перемещения вправо, имеем
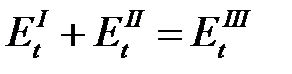 .
.
или

где  – расстояние от зарядов до любой точки А, находящейся на границе раздела диэлектриков. Отсюда
– расстояние от зарядов до любой точки А, находящейся на границе раздела диэлектриков. Отсюда
 (1)
(1)
Из условия равенства нормальных составляющих вектора D на границе раздела, приняв за положительное для нормали направление вниз, имеем

или
 ,
,
Откуда
 . (2)
. (2)
Решая совместно уравнения (1) и (2), получаем значения вспомогательных зарядов:
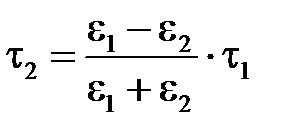 ;
;  .
.
|
из
5.00
|
Обсуждение в статье: Метод зеркальных изображений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

