 |
Главная |
Свойства предела функции
|
из
5.00
|
ПРЕДЕЛ ФУНКЦИИ
Число A называется пределом функции y = f(x) в точке x0, если для любого положительного числа e можно найти такое положительное число d, что для всех x из d-окрестности точки x0 соответствующие значения y попадают в e-окрестность точки y = A.
ИЛИ: Число A называется пределом функции y = f(x) в точке x0, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию 0 < êx – x0ê < d, выполняется условиеêy – Aê < e.
Тот факт, что A есть предел функции y = f(x) в точке x = x0, записывается формулой

|
 .
.
Очевидно, чтобы функция имела предел в точке x = x0, не требуется, чтобы она была определена в этой точке.
Рассмотрим функцию  . Очевидно, что если x > 0, то y = 2x; если x < 0, то y = –2x; при x = 0 функция не определена.
. Очевидно, что если x > 0, то y = 2x; если x < 0, то y = –2x; при x = 0 функция не определена.
График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.
Функция y = f(x) называется непрерывной в точке x = x0, если она определена в этой точке и ее значение f(x0) равно пределу функции в этой точке:  .
.
Функция y = x2 непрерывна в точке x = 2, как и во всех точках числовой оси. Функция  не является непрерывной в точке x = 2. Функция
не является непрерывной в точке x = 2. Функция 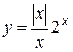 не является непрерывной в точке x = 0.
не является непрерывной в точке x = 0.
 Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.
Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.
Свойства предела функции
1. Функция не может иметь в одной точке два разных предела.
2.  , если C — постоянная функция.
, если C — постоянная функция.
3. Если существует  и C — постоянная функция, то
и C — постоянная функция, то  .
.
4. Если существуют  и
и  , то существует
, то существует  , равный
, равный  , а также существует
, а также существует  , равный
, равный  . Если при этом
. Если при этом  , то существует
, то существует  , равный
, равный  .
.
Введем определения так называемых “односторонних пределов”.
Число B называется пределом функцииf(x)в точкеaсправа (это записывается в виде формулы  ), если для любого положительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
), если для любого положительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
Согласно приведенному определению 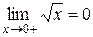 . Отметим, что обыкновенного предела функция
. Отметим, что обыкновенного предела функция  в точке x = 0 не имеет.
в точке x = 0 не имеет.
Число С называется пределом функцииf(x)в точкеbслева (это записывается в виде формулы  ), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
Функция f(x) называется непрерывной в точкеa справа (непрерывной в точке b слева), если
 (
(  ).
).
Функция  непрерывна справа в точке x=0.
непрерывна справа в точке x=0.
Функция называется непрерывной на замкнутом промежутке[a, b], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Достаточно просто можно доказать теорему, связывающую понятия предела функции в точке и односторонних пределов. Мы ограничимся только формулировкой теоремы.
Для того, чтобы выполнялось равенство  , необходимо и достаточно, чтобы одновременно выполнялись два равенства:
, необходимо и достаточно, чтобы одновременно выполнялись два равенства:
 ;
; 
В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f(x), определенную на полубесконечном промежутке (х0; ¥). Число А называется пределом функции f(x) при х, стремящемся к бесконечности:
 ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, превосходящих М, выполняется условие:
½f(x) – A½ < e.
Пусть теперь функция f(x) определена на полубесконечном промежутке
(–¥; х0). Число А называется пределом функции f(x) при х, стремящемся к минус бесконечности:
 ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, меньших, чем – М, выполняется условие:
½f(x) – A½ < e.
Отметим два, так называемых, "замечательных предела".
1.  . Геометрический смысл этой формулы заключается в том, что прямая
. Геометрический смысл этой формулы заключается в том, что прямая  является касательной к графику функции
является касательной к графику функции  в точке
в точке 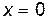 .
.
2.  . Здесь e — иррациональное число, приблизительно равное 2,72.
. Здесь e — иррациональное число, приблизительно равное 2,72.
Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S0 с условием, что через период времени T будет возвращена сумма ST. Определим величину r относительного роста формулой
 . (1)
. (1)
Относительный рост можно выразить в процентах, умножив полученное значение r на 100.
Из формулы (1) легко определить величину ST:
ST = S0(1 + r)
При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S0 возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма S1 = S0(1 + r), то есть S2 = S0(1 + r)2. Аналогично получается S3 = S0(1 + r)3. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:
Sn = S0(1 + r)n.
В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k. Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка Tk составляет  часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма ST рассчитывается по формуле
часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма ST рассчитывается по формуле
 (2)
(2)
Здесь  — целая часть числа
— целая часть числа  , которая совпадает с самим числом, если, например, T ‑ целое число.
, которая совпадает с самим числом, если, например, T ‑ целое число.
Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S0 наращивается до величины, определяемой формулой
 (3)
(3)
В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции ST и S1. Применим эту процедуру к формуле (3):
 .
.
Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S0 за 1 год наращивается до величины S1*, которая определяется из формулы
S1* = S0er. (4)
Пусть теперь сумма S0 предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим re годовую ставку, при которой в конце года сумма S0 наращивается до величины S1* из формулы (4). В этом случае будем говорить, что re — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении.Из формулы (3) получаем
 .
.
Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и re:
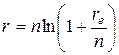 ,
,  .
.
Эти формулы широко используются в финансовых расчётах.
|
из
5.00
|
Обсуждение в статье: Свойства предела функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

