КОНСПЕКТ ЛЕКЦИИ «КОМПЛЕКСНЫЕ ЧИСЛА»

 

План лекции:

1. Числовые множества.

2. Основные понятия множества комплексных чисел.

3. Геометрическое изображение комплексных чисел.

4. Формы записи комплексных чисел

5. Действия над комплексными числами, представленными в алгебраической форме:

5.1. сложение;

5.2. вычитание;

5.3. умножение;

5.4. деление.

6. Действия над комплексными числами, представленными в тригонометрической и показательной форме:

6.1. умножение;

6.2. возведение в степень;

6.3. деление;

6.4. извлечение корня.

 

1. Числовые множества

 

Натуральные числа – это числа, которые используются для пересчета предметов: 1, 2, 3, … Все натуральные числа можно записать как множество:

Натуральные числа можно писать со знаком (+) : 1 = + 1; 2 = + 2; 3 = + 3, ... . Числа +1, +2, +3, ... - это целые положительные числа.

Натуральные числа со знаком минус ( - ) -1, -2, -3, ... - это целые отрицательные числа.

0 - это тоже целое число (не положительное и не отрицательное ).

Все целые числа можно записать как множество:

Z = {... -3, -2, -1, 0, 1, 2, 3, ... }.

Дробные числа, как и целые, могут быть положительные и отрицательные.

Например, ; ; 0,7; +1,18; - 3,485.

Конечные дроби – это рациональные числа.

Все рациональные числа можно записать как множество:

Иррациональные числа - это бесконечные непериодические десятичные дроби. Например, число - (пи): = 3,141592... - это иррациональное число. Множество иррациональных чисел обозначают буквой J.

Все рациональные и иррациональные числа - это действительные числа. Множество действительных чисел обозначают буквой R.

Действительные числа - это положительные числа, отрицательные числа и 0: .

2. Основные понятия

 

Комплексным числом zназывается выражение вида z = x + iy, где х и у - действительные числа, a i - так называемая мнимая единица, i² = -1.

 

Число х называется действительной частьюкомплексного числа z и обозначается х = Re z. а у - мнимой частью z, у = Im z.

 

Если х = 0, то число 0 + iy = iy называется чисто мнимым; если у = 0, то число х + i0 = х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. е. R С.

Два комплексных числа z₁ = х₁ + iy₁ и z₂ = x₂ + iy₂ называются рав­ными (z₁ = z₂) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х₁ = х₂, у₁ = у₂. В частности, комплекс­ное число z = х + iy равно нулю тогда и только тогда, когда х = у = 0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Два комплексных числа z = х + iy и = х - iy, отличающиеся лишь знаком мнимой части, называются сопряженными.

Два комплексных числа z = х + iy и -z =- х - iy, отличающиеся знаком, называются противоположными.

 

3. Геометрическое изображение комплексных чисел

 

Всякое комплексное число z = x + iy можно изобразить точкой М(х; у) плоскости Оху такой, что х = Rez, у = Imz. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассма­тривать как образ комплексного числа z = x + iy (см. рис. 1).

 

Рис. 1.

 

Плоскость, на которой изображаются комп­лексные числа, называется комплексной плос­костью. Ось абсцисс называется действи­тельной осью, так как на ней лежат действи­тельные числа z = х + 0i = х. Ось ординат назы­вается мнимой осью, на ней лежат чисто мни­мые комплексные числа
z = 0 + iy = iy.

Комплексное число z = x + iy можно задавать с помощью радиус-вектора = = 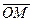(х;у).

Длина вектора , изображающего комплексное число z, называется модулемэтого числа и обозначается |z| или r.

Ве­личина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументомэтого комплексного числа, обозначается Arg z или φ.

Аргумент комплексного числа z = 0 не определен. Аргумент комплекс­ного числа z ≠ 0 - величина многозначная и определяется с точностью до слагаемого 2πk (к = 0, -1,1, -2,2...): Arg z = arg z + 2πk, где arg z - главное значение аргумента, заключенное в промежутке ( - π; π], т. е. - π < arg z ≤ π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2π)).

 

4. Формы записи комплексных чисел

 

Запись числа z в виде z = х + iy называют алгебраической формойкомплексного числа.

Модуль r и аргумент φ комплексного числа можно рассматривать как полярные координаты вектора = 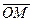,изображающего комплексное число z = х + iy (см. рис. 2).

Тогда получа­ем х = r cos φ, у = r sin φ. Следовательно, ком­плексное число z = х + iy можно записать в виде z = r cos φ + ir sin φ или

z = r (cos φ + i sin φ).

Такая запись комплексного числа называется тригонометрической формой.

 

Рис. 2.

 

Модуль r = |z| однозначно определяется по формуле

Аргумент φ определяется из формул , , .

Так как φ = Arg z = arg z + 2kπ,

то cos φ = cos(arg z + 2kπ) = cos(arg z), sin φ = sin(arg z).

Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение ар­гумента комплексного числа z, т. е. считать φ = arg z.

Так как - π < arg z ≤π, то из формулы -получаем, что

Если точка z лежит на действительной или мни­мой оси, то arg z можно найти непосредственно (см. рис. 3).

 

Пример.
arg z₁ = 0 для z₁ = 2;
arg z₂ = π для z₂ = -3;
arg z₃ = π/2 для z₃ = i;
arg z₄ = -π/2 для z₄ = -8i

 

 

Рис. 3.

 

 

 

Используя формулу Эйлера: e^iφ = cos φ + i sin φ,

комплексное число z = r(cos φ + i sin φ) можно записать в так назы­ваемой показательной(или экспоненциальной) форме z = re^iφ,

где r = |z| - модуль комплексного числа, а угол φ = arg z = arg z + 2kπ (k = 0,-1,1,-2,2...).

В силу формулы Эйлера, функция e^iφ периодическая, с основным пери­одом 2π. Для записи комплексного числа z в показательной форме, доста­точно найти главное значение аргумента комплексного числа, т. е. считать φ = aig z.

Пример. Записать комплексные числа z₁ = -1 + i и z₂ = - 1 в тригонометрической и показательной формах.

 

Решение: Для z₁ имеем

Для z₂ имеем , arg z = arg(-1) = π

т. е. φ = π. Поэтому -1 = cos π + i sin π = е^iπ.

 

5. Действия над комплексными числами, представленными
в алгебраической форме

 

5.1. Сложение комплексных чисел

 

Суммойдвух комплексных чисел z₁ = х₁ + iy₁ и z₂ = х₂ + iy₂ называется комплексное число, определяемое равенством

z₁+ z₂ = (x₁ + x₂) + i(y₁ + у₂).

Свойства суммы комплексных чисел:

· переместителъное(коммутативное) z₁ + z₂ = z₂ + z₁ ,

· сочетатель­ное(ассоциативное) (z₁ + z₂) +z₃ = z₁ + (z₂ + z₃).

Геометрически (см. рис. 4). комплексные числа складываются как векторы.

 

 

Рис. 4.

 

Непосредственно из рисунка видно, что |z₁ + z₂| ≤ |z₁| + |z₂|. Это соот­ношение называется неравенством треугольника.

 

5.2. Вычитание комплексных чисел

 

Вычитание определяется как действие, обратное сложению.

Разностьюдвух комплексных чисел z₁ и z₂ называется такое комплексное число z, которое, будучи сложенным с z₂, дает число z₁, т. е. z = z₁ - z₂, если z + z₂ = z₁. Если z₁ = х₁ + iy₁, z₂ = х₂ + iy₂, то из этого определения легко полу­чить z:

z = z₁ – z₂ = (x₁ – x₂) + i(y₁ – y₂).

Геометрически комплексные числа вычи­таются как векторы (см. рис. 5).

 

 

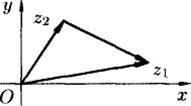
Рис. 5.

 

 

Непосредственно из рисунка видно, что |z₁ - z₂\ ≥ |z₁| - |z₂|.

Отметим, что , т. е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.

Поэтому, например, равенство |z - 2i| = 1 определяет на комплекс­ной плоскости множество точек z, находящихся на расстоянии 1 от точки z₀ = 2i, т. е. окружность с центром в z₀ = 2i и радиусом 1.

 

5.3. Умножение комплексных чисел

 

Произведениемкомплексных чисел z₁ = x₁ + iy₁ и z₂ = х₂ + iy₂ называется комплексное число, определяемое равенством

z = z₁z₂ = (x₁x₂ – y₁y₂) + i(х₁у₂ + y₁x₂).

 

Отсюда, в частности, следует важнейшее соотношение i² = -1.

Действительно, i² = ii = (0 + 1i)(0 + 1i) = (0 - 1) + i(0 + 0) = -1.

Формула умножения получается формально путем перемножения двучленов х₁ + iy₁ и х₂ + iу₂:

(x₁ + iy₁)(x₂ + iy₂) = x₁x₂ + x₁iy₂ + iy₁x₂ + iy₁iy₂ = x₁x₂ + i²y₁y₂ + i(x₁y₂ + у₁х₂) = x₁x₂ - у₁у₂ + i(х₁у₂ + y₁x₂)

Заметим, что z = (х + iу)(х - iу) = х² + у² - действительное число.

 

Умножение комплексных чисел обладает свойствами:

· переместительным z₁z₂ = z₂z₁;

· сочета­тельным (z₁z₂)z₃ = z₁(z₂z₃);

· распределительным (дистрибутивным) z₁(z₂ +z₃) = z₁z₂ + z₁z₃.

 

5.4. Деление комплексных чисел

 

Деление определяется как действие, обратное умножению.

Частным двух комплексных чисел z₁ и z₂ ≠ 0 называется комплексное число z, которое, будучи умноженным на z₂, дает число z₁, т.е. = z, если z₂z = z₁. Таким образом,

 

Если положить z₁ = x₁ + iy₁, z₂ = x₂ + iy₂ ≠ 0, z = х + iу, то из равенства
(x₂ + iy₂)(х + iy) = x₁ + iy₁ следует

Решая систему, найдем значения х и y:

,

Таким образом,

 

 

На практике частное двух комплексных чисел находят путем умноже­ния числителя и знаменателя на число, сопряженное знаменателю («из­бавляются от мнимости в знаменателе»).

 

Пример. Выполнить деление .

Решение: