 |
Главная |
ЛАБОРАТОРНАЯ РАБОТА № 3. ИССЛЕДОВАНИЕ ЗАКОНОВ ПОСТОЯННОГО ТОКА
|
из
5.00
|
ИССЛЕДОВАНИЕ ЗАКОНОВ ПОСТОЯННОГО ТОКА
Цель работы: исследование зависимости величины UR (падения напряжения на внешнем сопротивлении цепи) от величины силы тока; определение ЭДС и внутреннего сопротивления источника; изучение зависимости между Р, полной мощностью всей цепи; PR, мощностью внешней части цепи; Рr, мощностью внутри источника, КПД источника и внешним сопротивлением R .
Приборы и оборудование: установка для изучения законов постоянного тока.
Теоретические сведения
Работа по переносу электрического заряда определяется по формуле
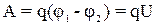
Так как величина заряда q=It, то работа электрического тока на участке цепи
A = UIt.
Для однородного участка цепи U=IR, т.е.
A =I2Rt= 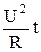
Так как мощность 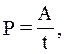 то P=IU; для однородного участка цепи
то P=IU; для однородного участка цепи
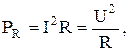 (1)
(1)
где PR - мощность, выделяемая во внешней части цепи, обладающей сопротивлением R.
Учитывая закон Ома для замкнутой цепи
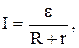
получим выражение
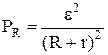 . (2)
. (2)
Взяв производную 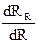 и приравняв ее к нулю, найдем, что PR будет иметь максимальное значение при R=r,т.е. когда внешнее сопротивление цепи равно внутреннему сопротивлению источника. В замкнутой цепи работу совершают только сторонние силы. По определению ЭДС
и приравняв ее к нулю, найдем, что PR будет иметь максимальное значение при R=r,т.е. когда внешнее сопротивление цепи равно внутреннему сопротивлению источника. В замкнутой цепи работу совершают только сторонние силы. По определению ЭДС
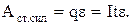
Полная мощность всей замкнутой цепи
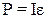
Учитывая закон Ома для замкнутой цепи, получим выражение
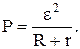 (3)
(3)
Коэффициент полезного действия источника тока рассчитывается по формуле
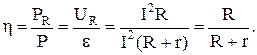 (4)
(4)
Для исследования законов постоянного тока применяется установка, схема которой изображена на рис. 1 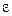 - источник тока; mA – миллиамперметр для измерения тока; V – вольтметр для измерения напряжения на внешнем резисторе;
- источник тока; mA – миллиамперметр для измерения тока; V – вольтметр для измерения напряжения на внешнем резисторе; 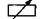 - магазин резисторов, при помощи которого можно устанавливать необходимое сопротивление).
- магазин резисторов, при помощи которого можно устанавливать необходимое сопротивление).
По закону Ома для замкнутой цепи
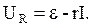 (5)
(5)

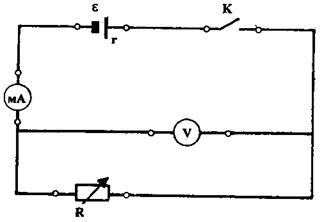
Рис. 1
График зависимости UR(I), см. рис. 2, есть прямая линия, отсекающая на оси UR значение, равное ЭДС источника ε, а на оси I-значение, равное силе тока короткого замыкания 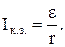
Внутреннее сопротивление источника –
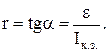
Мощность внешней части цепи (полезная мощность) –
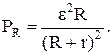
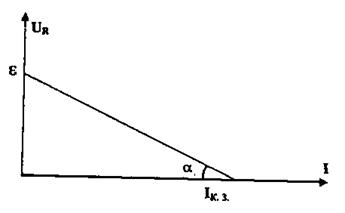
Рис. 2
Графиком зависимости PR(R), см. рис. Заявляется кривая линия, имеющая экстремальную точку при R=r и асимптотически приближающаяся к оси сопротивления R:
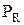 →0 при R→0;
→0 при R→0;
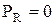 при R=0
при R=0
Полная мощность равна 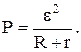
Графиком зависимости Р(R) является гипербола (рис. 4):
При R→0 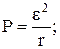
При R→∞ Р→0.
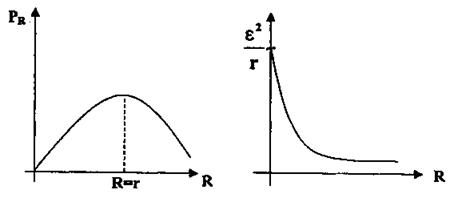
Рис. 3 Рис. 4
Коэффициент полезного действия источника тока 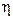 определяется по формуле (4)
определяется по формуле (4)
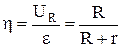
и имеет график, асимптотически приближающийся к горизонтальной прямой 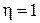 ; при R→∞
; при R→∞ 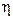 →1 (рис. 5).
→1 (рис. 5).
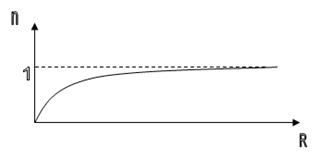
Рис.5
Порядок выполнения работы
1.Собрать рабочую схему (рис. 1) на тренаже и показать ее преподавателю.
2. Получив допуск, подойти к готовой установке и замкнуть цепь ключом К.
3. На магазине резисторов установить сопротивления R, равные 10, 20, 30 Ом
и т.д. Выбрать 30 точек, записывая при этом показания миллиамперметра и
вольтметра в таблицу.
Таблица
| R | I | 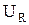
| 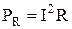
| 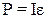
| 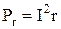
| 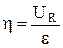
|
4. По данным таблицы построить график зависимости 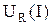 так, чтобы число
так, чтобы число
экстремальных точек, лежащих ниже и выше этой прямой, было одинаково.
Разброс точек происходит из-за случайных явлений, сопровождающих процесс измерения.
5. По графику определить ЭДС источника ε и внутреннее сопротивление г, учитывая, что 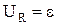 при I=0,
при I=0, 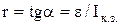
6. Провести дополнительные измерения I и 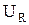 при R=r и в окрестности этой
при R=r и в окрестности этой
точки через 2 Ома.
7. Заполнить нее графы таблицы по расчетным формулам, указанным в ней.
8. По данным таблицы построить графики зависимостей P(R), PR(Р), Pr(R)
9. По данным таблицы построить графики зависимости 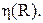
10.Сравнить полученные экспериментальные кривые с теоретическими
кривыми.
Контрольные вопросы
1.Дать понятие мощности тока и назвать единицы ее измерения.
2. Какие виды мощности вы знаете? Дать их краткую характеристику.
3. От чего зависит КПД источника тока?
4. По графику (рис. 6) определить зависимость UR(I), ЭДС источника 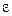 , силу
, силу
тока короткого замыкания 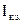 ; внутреннее сопротивление источника г, силу
; внутреннее сопротивление источника г, силу
тока и падение напряжения, при которых мощность, выделяемая на внешнем
резисторе, будет максимальной.
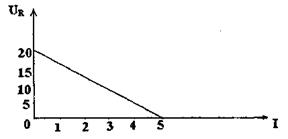
Рис. 6
5. На координатной плоскости изображены 3 графика (рис. 7). Указать, какой из них соответствует графикам зависимости: Pr(R ) - полезной мощности от внешнего сопротивления, P(R ) - полной мощности от внешнего сопротивления, 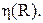 КПД источника от внешнего сопротивления.
КПД источника от внешнего сопротивления.
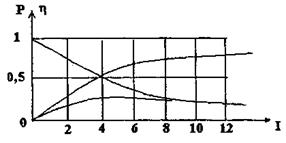
Рис. 7
Определить по этим графикам ЭДС источника ε, внутреннее сопротивление источника r и записать аналитическое выражение зависимостей P(R), PR(R ), 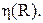
6. Как изменятся графики зависимостей PR(R), UR(I), PR(I), если внутреннее сопротивление источника увеличится вдвое? Почему лампочка в 3,5 В не горит при подключении ее к батарее «Крона» - источнику питания для транзисторных приемников (ЭДС источника равна 9В)?
ЛАБОРАТОРНАЯ РАБОТА 4
ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА С ПОМОЩЬЮ
ЭЛЕКТРОННОГО ВОЛЬТМЕТРА
Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов.
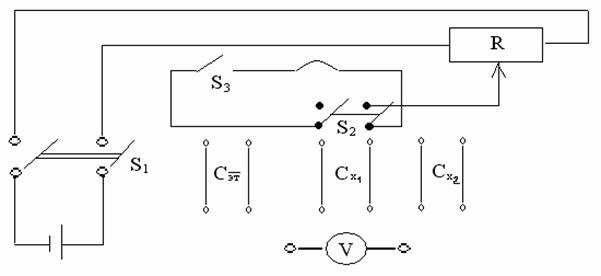
Приборы и оборудование: источник питания ( 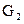 ), электронный вольтметр (В7-16А), потенциометр (R14), эталонный конденсатор (Сэт), исследуемый конденсатор (Сх), переключатель (S4 ).
), электронный вольтметр (В7-16А), потенциометр (R14), эталонный конденсатор (Сэт), исследуемый конденсатор (Сх), переключатель (S4 ).
Теоретические сведения
Опытным путем было установлено, что в природе существует два типа электрических зарядов, условно названных положительными и отрицательными. Одноименные заряды отталкиваются друг от друга, разноименные притягиваются.
Р, Милликеи доказал, что электрический заряд дискретен, т.е. величина заряда любого тела составляет целое число, кратное элементарному электрическому заряду е (e=1,6∙10-19 Кл). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
В результате обобщения опытных данных был сформулирован фундаментальный закон природы - закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри нее.
Единица электрического заряда, 1 кулон (Кл), - это электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за время, рапное 1с :
1Кл=1 А∙1с.
Закон взаимодействия неподвижных точечных электрических зарядов был открыт Кулоном: сила взаимодействия F двух точечных зарядов прямо пропорциональна величине зарядов q1 и q2 и обратно пропорциональна квадрату расстояния г между ними:
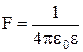 ∙
∙ 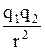 (1)
(1)
где  - электрическая постоянная;
- электрическая постоянная; 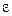 - диэлектрическая проницаемость среды (безразмерная величина).
- диэлектрическая проницаемость среды (безразмерная величина).
Напряженность 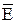 электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:
электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:
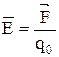
Направление вектора 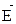 совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряженности электрического поля:
совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряженности электрического поля:
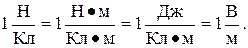
Графически электростатическое поле изображают с помощью линий напряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженности (рис. I).
Величина
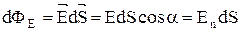
называется потоком вектора напряженности через площадку dS. Здесь dS = dSn - вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке ( 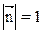 ).
).
Электростатические поля подчиняются принципу суперпозиции: напряженность 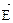 результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:
результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:
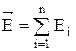 (3)
(3)
где 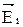 - напряженность электростатического поля, созданного i-м зарядом.
- напряженность электростатического поля, созданного i-м зарядом.
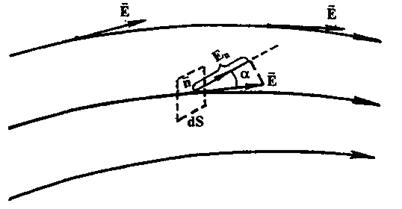
Рис. 1
Теорема Остроградского-Гаусса для электростатического поля в вакууме звучит так: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на eq:
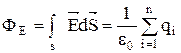 (4)
(4)
Из теоремы Гаусса следует, что напряженность электростатического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями в вакууме будет равна
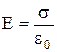 , (5)
, (5)
где 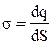 - поверхностная плотность заряда плоскостей.
- поверхностная плотность заряда плоскостей.
Если между заряженными плоскостями находится изолятор с диэлектрической проницаемостью 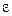 , то напряженность поля внутри него уменьшается в
, то напряженность поля внутри него уменьшается в 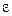 раз (рис. 2):
раз (рис. 2):
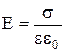 (6)
(6)
Электростатическое поле является полем консервативных сил, т.е. работа, совершаемая силами поля по перемещению электрического заряда из одной точки пространства в другую, не зависит от траектории движения заряда, а определяется только его начальным и конечным положениями. Для такого рода полей можно ввести понятие потенциальной энергии заряда, численно равной работе, совершаемой силами электростатического поля по перемещению его ич данной точки пространства в другую (ту, в которой потенциальная энергия заряда равна нулю).
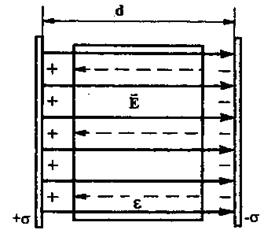
Рис. 2
Как правило, потенциальная энергия заряда, удаленного в бесконечность, считается равной нулю. Поэтому она будет равна
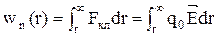 , (7)
, (7)
где 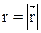 - модуль радиус-вектора
- модуль радиус-вектора 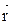 ;
; 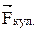 - кулоновская сила;
- кулоновская сила; 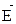 - напряженность электростатического поля; qo - электрический заряд.
- напряженность электростатического поля; qo - электрический заряд.
Если заряд q0 перемещается из первой точки во вторую(определяются соответственно радиус-векторами 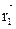 и
и 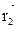 то работу, совершаемую силами поля, можно найти как разность работ
то работу, совершаемую силами поля, можно найти как разность работ
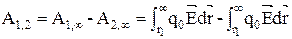
A 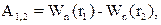 (8)
(8)
где 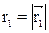 и
и 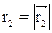 ;
; 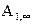 и
и 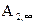 - работы, совершаемые силами поля при перемещении заряда из первой и второй точек в бесконечность.
- работы, совершаемые силами поля при перемещении заряда из первой и второй точек в бесконечность.
Потенциал - физическая величина, определяемая работой сил поля по перемещению единичного положительного заряда из данной точки в бесконечность:
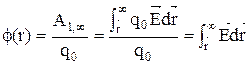
Единица потенциала - вольт (В): 1 В - потенциал такой точки поля, в которой заряд в 1Кл обладает потенциальной энергией в 1 Дж:
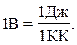
Поскольку 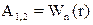 , то
, то
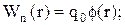
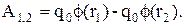 (10)
(10)
Отсюда
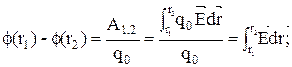
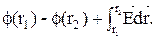 (11)
(11)
Зная потенциал в каждой точке пространства 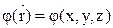 можно найти напряженность электростатического поля:
можно найти напряженность электростатического поля:
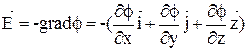 (12)
(12)
Знак «минус» указывает на то, что вектор напряженности Ё направлен в сторону убывания потенциала.
Потенциал уединенного проводника прямо пропорционален его заряду;
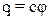
При этом величину 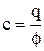 (13)
(13)
называют электроемкостью уединенного проводника. Единица электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1Кл, т.е.
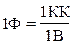
Для накопления значительных зарядов служат конденсаторы, состоящие из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы подразделяются на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению накопленного заряда q к разности потенциалов 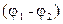 между обкладками:
между обкладками:
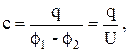
где 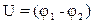 напряжение между обкладками. Плоский конденсатор обладает емкостью
напряжение между обкладками. Плоский конденсатор обладает емкостью
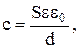
где 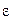 - диэлектрическая проницаемость изолятора;
- диэлектрическая проницаемость изолятора;  - электрическая постоянная; S - площадь обкладки; d - расстояние между обкладками.
- электрическая постоянная; S - площадь обкладки; d - расстояние между обкладками.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи параллельно или последовательно. У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна 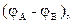 см рис. 3.
см рис. 3.
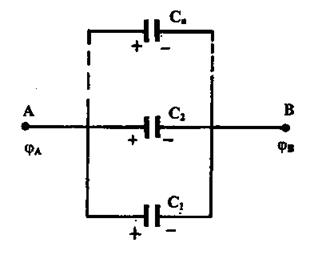
Если емкости отдельных конденсаторов 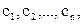 то их заряды равны соответственно
то их заряды равны соответственно
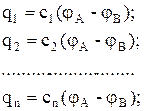
а заряд батареи конденсаторов-
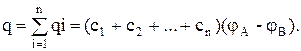
Полная емкость батареи –
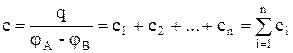 , (16)
, (16)
т.е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
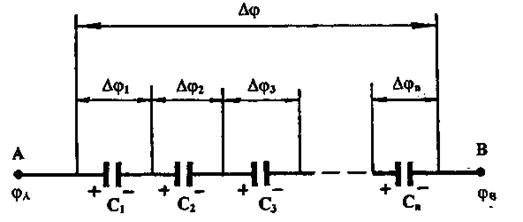
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи, см. рис. 4, равна
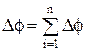 .
.
Причем для любого из рассматриваемых конденсаторов
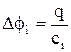 .
.
С другой стороны,
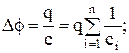
откуда 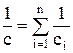 , (17)
, (17)
т.е. при последовательном соединении конденсаторов суммируются обратные величины емкостей.
Если дана емкость эталонного конденсатора Сэт, то неизвестную емкость другого конденсатора Сх можно определить следующим образом.
Сначала конденсатор Сэт зарядить от источника постоянного тока (рис.5а). При этом накапливается заряд q. С помощью вольтметра измерить напряжение на обкладках конденсатора:
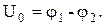
Тогда
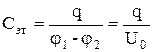 .
.
Отсюда
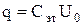 . (18)
. (18)
Затем эталонный конденсатор отключить от источника питания и к нему параллельно присоединить конденсатор неизвестной емкости Сх (рис. 5б). Электрический заряд q распределится по конденсаторам Сэт и Сх.
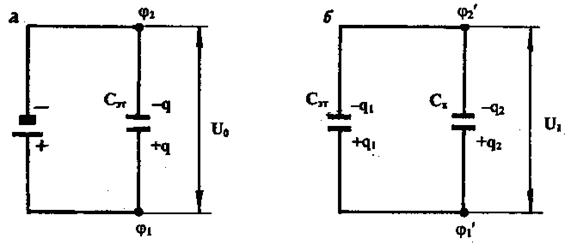
Согласно закону сохранения зарядов в замкнутой системе
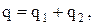 (19)
(19)
где q1, q2- электрические заряды на конденсаторах Сэти Сх.
После этого измерить напряжение 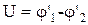 на обкладках конденсаторов, причем
на обкладках конденсаторов, причем
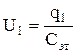 и
и 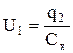 .
.
Отсюда
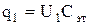 и
и 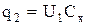 . (20)
. (20)
Поэтому
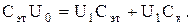
В результате 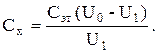 (21)
(21)
Порядок выполнения работы
1. Тумблером включить установку.
2. Клеммы Сэт проводниками соединить с клеммами переключателя S2.
3. Переключателем S включить напряжение от источника питания на эталонном конденсаторе.
4. Установить движком потенциометра R на напряжение U0=(1±0,2) В. Снять показания вольтметра.
5. Переключателем S2 отключить эталонный конденсатор от источника питания.
6. Соединить проводниками Сэт и Сх1 параллельно и снять показания вольтметра U1.
7. Тумблером S3 разрядить конденсаторы.
8. Подавая на эталонный конденсатор напряжение от 1 В до 1,4 В, провести измерения 3 раза. Данные занести в таблицу.
9. Для каждой пары значений напряжений U0 и U1 найти электроемкость по формуле
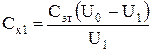 .
.
Затем определить среднюю величину электроемкости Сх1(ср). Результаты вычислений занести в таблицу.
10. По п.п. 3-9 найти электроемкость Сх2.
Таблица
| U0 | U1 | Cx1 | U0 | U2 | Cx2 | U0 | Uпар | Cпар | U0 | Uпосл | Cпосл |
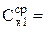
| 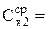
| 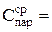
| 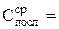
|
11. Соединить конденсаторы Сх1 и Сх2 параллельно.
12. По п.п. 3-9 найти электроемкость батареи Спар.
13. Соединить конденсаторы Сх1 и Сх2 последовательно.
14. По п.п. 3-9 найти электроемкость батареи Спосл.
По формулам 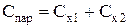 и
и 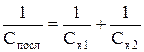 вычислить емкость батареи последовательно и параллельно соединенных конденсаторов и сравнить результаты с экспериментальными значениями.
вычислить емкость батареи последовательно и параллельно соединенных конденсаторов и сравнить результаты с экспериментальными значениями.
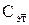 =1000 мкФ.
=1000 мкФ.
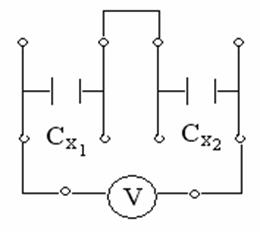
| Последовательно |
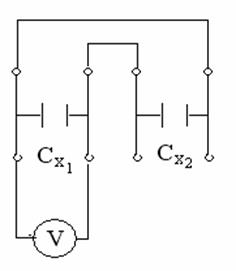
| Параллельно |
ЛАБОРАТОРНАЯ РАБОТА 5
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ
ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Цель работы: определение горизонтальной составляющей индукции магнитного поля Земли при помощи тангенс-буссоли.
Приборы и оборудование: тангенс-буссоль, миллиамперметр, резистор, источник питания, коммутатор.
Теоретические сведения
Подобно тому как в пространстве, окружающем электрические заряды, возникает электростатическое поле, в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Особенностью магнитного поля является то, что оно действует только на движущиеся электрические заряды. Характер влияния магнитного поля на электрический ток зависит от формы проводника, его расположения и направления тока.
При исследовании магнитного поля используются магнитная стрелка или замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до проводника с током, образующего магнитное поле. Ориентация контура характеризуется направлением нормали к нему. В качестве положительного принимается направление, связанное с правилом правого винта, т.е. направление поступательного движения винта, головка которого вращается в направлении тока, идущего по рамке (рис. 1). За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная к рамке нормаль.
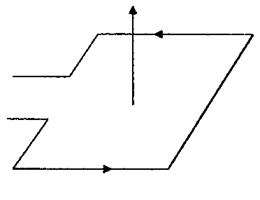
Рис. 1
Рамка с током испытывает ориентирующее влияние поля, т.к. на нее действует пара сил. Вращающий момент сил определяется векторным произведением 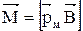 , где
, где 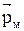 - вектор магнитного момента рамки с током;
- вектор магнитного момента рамки с током; 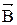 - вектор магнитной индукции. Индукция магнитного поля является силовой характеристикой поля,
- вектор магнитной индукции. Индукция магнитного поля является силовой характеристикой поля,
Для плоского контура с током
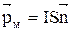 (1)
(1)
где I - сила тока; S - площадь контура; 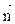 - единичный вектор нормали к поверхности рамки.
- единичный вектор нормали к поверхности рамки.
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с силой тока, равной единице, когда нормаль к рамке перпендикулярна направлению поля. За единицу магнитной индукции принята индукция такого поля, в котором на контур площадью 1м2 при силе тока 1А со стороны поля действует максимальный момент сил 1 Н∙м. Эта единица - тесла (Тл):
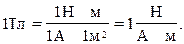
Линии, касательные к которым в каждой точке совпадают с направлением вектора 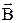 , называют силовыми линиями магнитной индукции. Величина магнитной индукции прямо пропорциональна числу силовых линий, пересекающих единицу площади. Их направление определяется правилом правого винта: головка винта, ввинчиваемого в направлении тока, вращается в направлении линий магнитной индукции (рис. 2).
, называют силовыми линиями магнитной индукции. Величина магнитной индукции прямо пропорциональна числу силовых линий, пересекающих единицу площади. Их направление определяется правилом правого винта: головка винта, ввинчиваемого в направлении тока, вращается в направлении линий магнитной индукции (рис. 2).
Линии индукции магнитного поля, созданного катушкой с током, показаны на рис. 3.
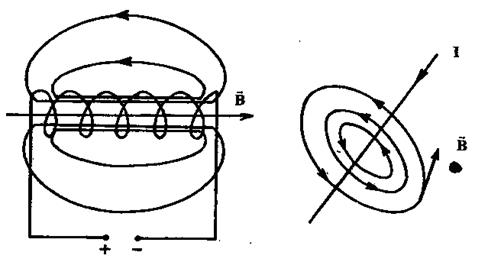
Рис. 2 Рис. 3
Эти линии всегда замкнуты и охватывают проводники с током. Поле, обладающее замкнутыми силовыми линиями, называется вихревым.
Магнитное поле постоянных токов изучалось Био и Саваром; окончательная формулировка найденного ими закона принадлежит Лапласу. Поэтому этот закон носит название закона Био-Савара-Лапласа.
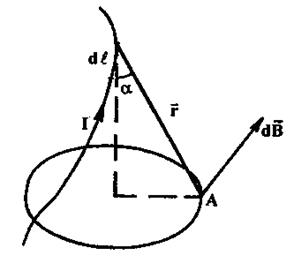
Рис. 4
Закон Био-Савара-Лапласа для проводника с током I, элемент 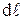 которого создает в некоторой точке А (рис. 4) индукцию поля dB записываются в виде:
которого создает в некоторой точке А (рис. 4) индукцию поля dB записываются в виде:
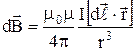 , (2)
, (2)
где 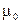 - магнитная постоянная
- магнитная постоянная 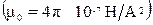 ;
; 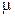 - магнитная проницаемость среды;
- магнитная проницаемость среды; 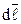 - вектор, по модулю равный длине
- вектор, по модулю равный длине 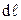 элемента проводника и совпадающий по направлению с током;
элемента проводника и совпадающий по направлению с током; 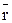 - радиус-вектор, проведенный из элемента проводника
- радиус-вектор, проведенный из элемента проводника 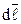 в некоторую точку А поля. Направление
в некоторую точку А поля. Направление 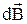 перпендикулярно плоскости, натянутой на
перпендикулярно плоскости, натянутой на 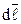 и
и 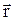 .
.
Модуль вектора В определяется выражением
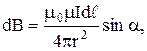 (3)
(3)
где 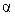 - угол между вектором
- угол между вектором 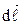 и радиус-вектором г.
и радиус-вектором г.
Для магнитного поля справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых каждым током или движущимся зарядом в отдельности.
Согласно принципу суперпозиции
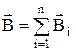 (4)
(4)
Если распределение тока симметрично, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать индукцию магнитного поля.
Согласно предположению Ампера в любом теле существуют микроскопические токи (микротоки), обусловленные движением электронов в атомах. Они создают свое магнитное поле и ориентируются в магнитных полях макротоков. Макроток - это ток в проводнике под действием ЭДС или разности потенциалов. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Магнитное поле макротоков описывается также и вектором напряженности Н. В случае однородной изотропной среды вектор магнитной индукции связан с вектором напряженности соотношением
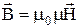 (5)
(5)
где μ0 - магнитная постоянная; μ- магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается или ослабляется за счет микротоков среды. Иначе говоря, μ показывает, во сколько раз вектор индукции магнитного поля в среде больше или меньше, чем в вакууме.
Единица напряженности магнитного поля - А/м. 1А/м - напряженность такого поля, магнитная индукция которого в вакууме равна 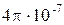 Тл. Земля представляет собой огромный шарообразный магнит. Действие магнитного поля Земли обнаруживается на ее поверхности и в окружающем пространстве.
Тл. Земля представляет собой огромный шарообразный магнит. Действие магнитного поля Земли обнаруживается на ее поверхности и в окружающем пространстве.
Магнитным полюсом Земли называют ту точку на ее поверхности, в которой свободно подвешенная магнитная стрелка располагается вертикально. Положения магнитных полюсов подвержены постоянным изменениям, что обусловлено внутренним строением нашей планеты. Поэтому магнитные полюса не совпадают с географическими. Южный полюс магнитного поля Земли расположен у северных берегов Америки, а Северный полюс - в Антарктиде. Схема силовых линий магнитного поля Земли показана на рис. 5 (пунктиром обозначена ось вращения Земли): 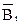 -горизонтальная составляющая индукции магнитного поля; Nr, Sr - географические полюсы Земли; N, S - магнитные полюсы Земли.
-горизонтальная составляющая индукции магнитного поля; Nr, Sr - географические полюсы Земли; N, S - магнитные полюсы Земли.
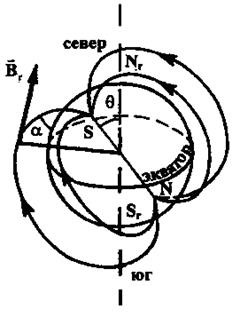
Рис. 5
Направление силовых линий магнитного поля Земли определяется с помощью магнитной стрелки. Если свободно подвесить магнитную стрелку, то она установится по направлению касательной к силовой линии. Так как магнитные полюсы находятся внутри Земли,магнитная стрелка устанавливается не горизонтально, а под некоторым углом а к плоскости горизонта. Этот угол a называют магнитным наклонением. С приближением к магнитному полюсу угол а увеличивается. Вертикальная плоскость, в которой расположена стрелка, называется плоскостью магнитного меридиана, а угол 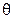 между магнитным и географическим меридианами - магнитным склонением. Силовой характеристикой магнитного поля, как уже отмечалось, является магнитная индукция В. Ее значение невелико и изменяется от 0,42∙10-4 Тл на экваторе до 0,7∙10-4 Тл у магнитных полюсов.
между магнитным и географическим меридианами - магнитным склонением. Силовой характеристикой магнитного поля, как уже отмечалось, является магнитная индукция В. Ее значение невелико и изменяется от 0,42∙10-4 Тл на экваторе до 0,7∙10-4 Тл у магнитных полюсов.
Вектор индукции магнитного поля Земли можно разделить на две составляющие: горизонтальную Вг и вертикальную 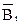 (рис. 5). Укрепленная на вертикальной оси магнитная стрелка устанавливается в направлении горизонтальной составляющей Земли
(рис. 5). Укрепленная на вертикальной оси магнитная стрелка устанавливается в направлении горизонтальной составляющей Земли 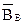 . Магнитное склонение 6, наклонение а и горизонтальная составляющая магнитного поля
. Магнитное склонение 6, наклонение а и горизонтальная составляющая магнитного поля 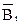 являются основными параметрами магнитного поля Земли.
являются основными параметрами магнитного поля Земли.
Значение 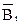 определяют магнитометрическим методом, который основан на взаимодействии магнитного поля катушки с магнитной стрелкой. Прибор, называемый тангенс-буссолью, представляет собой небольшую буссоль (компас с лимбом, разделенным на градусы), укрепленную внутри катушки 1 из нескольких витков изолированной проволоки.
определяют магнитометрическим методом, который основан на взаимодействии магнитного поля катушки с магнитной стрелкой. Прибор, называемый тангенс-буссолью, представляет собой небольшую буссоль (компас с лимбом, разделенным на градусы), укрепленную внутри катушки 1 из нескольких витков изолированной проволоки.
Катушка расположена в вертикальной плоскости. Она создает добавочное магнитное поле 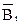 (диаметр катушки и число витков указываются на приборе).
(диаметр катушки и число витков указываются на приборе).
В центре катушки помещается магнитная стрелка 2. Она должна быть небольшой, чтобы можно было принимать индукцию, действующую на ее полюсы, равной индукции в центре кругового тока. Плоскость контура катушки устанавливается так, чтобы она совпадала с направлением стрелки и была перпендикулярна горизонтальной составляющей земного поля 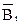 . Под действием
. Под действием 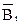 индукции поля Земли и индукции поля катушки стрелка устанавливается по направлению равнодействующей индукции
индукции поля Земли и индукции поля катушки стрелка устанавливается по направлению равнодействующей индукции 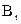 (рис. 6 а, б).
(рис. 6 а, б).
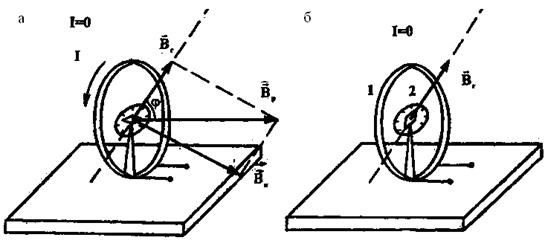
Рис. 6
Из рис. 6 видно, что
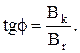 (6)
(6)
Индукция магнитного поля катушки в центре –
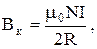 (7)
(7)
где N - число витков катушки; I - ток, идущий по ней; R - радиус катушки. Из (6) и (7) следует, что
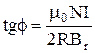 t
t
Или
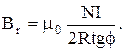 (8)
(8)
Важно понять, что формула (8) является приближенной, т.е. она верна только в том случае, когда размер магнитной стрелки намного меньше радиуса контура R. Минимальная ошибка при измерении фиксируется при угле отклонения стрелки ≈45°. Соответственно этому и подбирается сила тока в катушке тангенс-буссоли.
Порядок выполнения работы
1.Установить катушку тангенс-буссоли так, чтобы ее плоскость совпала с на
правлением магнитной стрелки.
2. Собрать цепь по схеме (рис. 7).
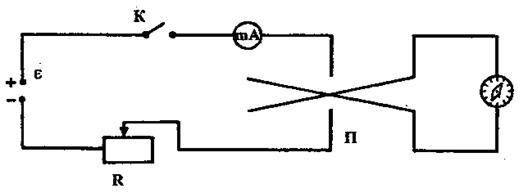
Рис. 7
3. Включить ток и измерить углы отклонения у концов стрелки 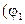 и
и 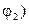 . С помощью переключателя П изменить направление тока на противоположное, не меняя величины силы тока, и измерить углы отклонения у обоих концов стрелки
. С помощью переключателя П изменить направление тока на противоположное, не меняя величины силы тока, и измерить углы отклонения у обоих концов стрелки 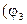 и
и 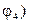 вновь. Таким образом устраняется ошибка, связанная с несовпадением плоскости катушки тангенс-буссоли с плоскостью магнитного меридиана. Вычислить
вновь. Таким образом устраняется ошибка, связанная с несовпадением плоскости катушки тангенс-буссоли с плоскостью магнитного меридиана. Вычислить
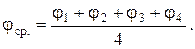
Результаты измерений I и 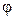 занести в таблицу.
занести в таблицу.
Таблица
| № | I, A | 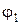
| 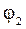
| 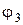
| 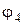
| 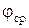
| 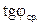
| 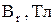
| 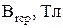
| 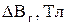
| ||
Популярное: Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас... Генезис конфликтологии как науки в древней Греции: Для уяснения предыстории конфликтологии существенное значение имеет обращение к античной...  ©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (3932)
|
Почему 1285321 студент выбрали МегаОбучалку... Система поиска информации Мобильная версия сайта Удобная навигация Нет шокирующей рекламы |
(0.009 сек.)

