 |
Главная |
Предел функции по Коши и по Гейне, их эквивалентность
|
из
5.00
|
6. Определение 1. (Предел функции по Коши) Предел функции  при
при  стремящемся к
стремящемся к 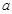 равен
равен  (записывается
(записывается  ), если для каждого положительного, сколь угодно малого числа
), если для каждого положительного, сколь угодно малого числа  найдется число
найдется число  , обладающее тем свойством, что при условии
, обладающее тем свойством, что при условии  выполнено условие
выполнено условие 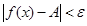 .
.
Запишем это определение в терминах математической логики: 
 .
.
7. Определение 2. (Предел функции по Гейне) Предел функции  при
при  стремящемся к
стремящемся к 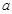 равен
равен  , если для каждой числовой последовательности такой, что
, если для каждой числовой последовательности такой, что  и
и  выполнено условие
выполнено условие  .
.
Запишем это определение в терминах математической логики: 
 .
.
8. Теорема 1. Определения 1 и 2 эквивалентны.
9. Доказательство. Пусть выполнены условия определения 1 и задано произвольное положительное число  . По определению 1 для него существует число
. По определению 1 для него существует число  , обладающее тем свойством, что при
, обладающее тем свойством, что при  выполнено соотношение
выполнено соотношение 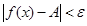 . Зафиксируем это число
. Зафиксируем это число  и рассмотрим произвольную числовую последовательность, члены которой
и рассмотрим произвольную числовую последовательность, члены которой  не равны числу
не равны числу  , и предел которой равен
, и предел которой равен  . Следовательно, для этого
. Следовательно, для этого  существует номер
существует номер  , обладающий тем свойством, что при
, обладающий тем свойством, что при  выполнено условие
выполнено условие  и
и  , т. е.
, т. е.  . Отсюда выполнено условие
. Отсюда выполнено условие  , а это и означает, что
, а это и означает, что  . Первая часть теоремы доказана.
. Первая часть теоремы доказана.
Пусть выполнены условия определения 2. Доказательство того, что выполнены условия определения 1 проведем методом «от противного». Если определение 1 не выполняется, то это означает, что существует положительное число  такое, что для любого числа
такое, что для любого числа  , например, для
, например, для 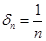 найдется соответствующее
найдется соответствующее  , обладающее тем свойством, что при условии
, обладающее тем свойством, что при условии  выполнено условие
выполнено условие  . А это означает, что построенная таким образом последовательность
. А это означает, что построенная таким образом последовательность  и в то же время не выполнено условие выполнено условие
и в то же время не выполнено условие выполнено условие  . Мы пришли в противоречие с тем, что выполнено определение 2. Теорема доказана.
. Мы пришли в противоречие с тем, что выполнено определение 2. Теорема доказана.
10. Теорема 2. Если предел функции существует, то он единственный.
11. Определение 3. Функции  называется бесконечно малой величиной в точке
называется бесконечно малой величиной в точке 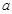 , если
, если  .
.
Итак, функция называется бесконечно малой (б. м.) в точке, если предел функции при подходе к этой точке равен 0.
12. Теорема 3. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая. Произведение б. м. величины (функции) на ограниченную величину (функцию) есть величина б. м. в этой же точке.
13. Доказательство совершенно аналогично доказательству теорем для последовательностей.
14. Теорема 4. Функции  имеет предел при
имеет предел при  стремящемся к
стремящемся к 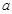 , равный
, равный  (записывается
(записывается  ), тогда и только тогда, когда функция
), тогда и только тогда, когда функция  является бесконечно малой величиной в точке
является бесконечно малой величиной в точке  .
.
15. Доказательство. Пусть  , т.е. при в силу определения Коши при соответствующих условиях
, т.е. при в силу определения Коши при соответствующих условиях 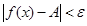 . Но это равносильно тому, что при тех же условиях
. Но это равносильно тому, что при тех же условиях  , т. е. функция
, т. е. функция  является б. м. величиной.
является б. м. величиной.
Под бесконечно большой величиной мы понимаем величину, обратная к которой является б. м.
|
из
5.00
|
Обсуждение в статье: Предел функции по Коши и по Гейне, их эквивалентность |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

