 |
Главная |
Напряженность электрического поля произвольного распределения зарядов
|
из
5.00
|
Формула— закон Кулона
где к коэффициент пропорциональности
q1,q2 неподвижные точечные заряды
r расстояние между зарядами

3. Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы  действующей на неподвижный[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда
действующей на неподвижный[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда  :
:  .
.
Напряжённость электрического поля точечного заряда
[править]В единицах СИ
Для точечного заряда в электростатике верен закона Кулона

Напряженность электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:

где каждое


4. При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
· результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
· Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
· Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
· Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.
В электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.
5. Работа электрического поля. 
6. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля  и потенциал
и потенциал  связаны соотношением[1]
связаны соотношением[1]

7. Принцип суперпозиции электростатических полей.Силы или поля от различных зарядов складываются с учетом их позиции или направленности (вектора). Это выражает принцип “суперпозиции” поля или потенциалов:потенциал поля нескольких зарядов равен алгебраической сумме потенциалов отдельных зарядов, φ=φ1+φ2+…+φn= ∑inφi. Знак потенциала совпадает со знаком заряда,φ=kq/r.
8. Потенциальная энергия заряда в электрическом поле. Продолжим сравнение гравитационного взаимодействия тел и электростатического взаимодействия зарядов. Тело массойm в поле тяжести Земли обладает потенциальной энергией.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком:
A = -(Wp2- Wp1) = mgh.
(Здесь и далее мы будем обозначать энергию буквой W.)
Точно так же, как тело массой m в поле силы тяжести обладает потенциальной энергией, пропорциональной массе тела, электрический заряд в электростатическом поле обладает потенциальной энергией Wp, пропорциональной заряду q. Работа сил электростатического поля А равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

9. Теорема о циркуляции вектора напряженности в интегральной форме: 
В дифференциальной форме: 
10. Связь потенциала и напряженности. E= - grad  = -Ñ
= -Ñ  .
.
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность Eнаправлена в сторону убывания потенциала
11. Поток вектора напряженности. 
|
| ||||

|
| ||||

|
|
Теорема Гаусса в интегральной форме:  где
где
·  — поток вектора напряжённости электрического поля через замкнутую поверхность
— поток вектора напряжённости электрического поля через замкнутую поверхность  .
.
·  — полный заряд, содержащийся в объёме, который ограничивает поверхность
— полный заряд, содержащийся в объёме, который ограничивает поверхность  .
.
·  — электрическая постоянная.
— электрическая постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
В дифференциальной форме:  Здесь
Здесь  — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а
— объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а  — оператор набла.
— оператор набла.
12. Применение закона Гаусса.1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность  заряда в любой точке сферы будет одинакова.
заряда в любой точке сферы будет одинакова.

a. Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
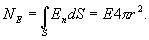
По теореме Гаусса

Следовательно

| (13.8) |
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
b. Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

| (13.9) |
c. Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е.  Следовательно, по теореме Гаусса,
Следовательно, по теореме Гаусса, 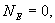 и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.
и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.

Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью  .
.

Проведем коаксиальную цилиндрическую поверхность радиуса 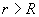 Поток вектора напряженности через эту поверхность
Поток вектора напряженности через эту поверхность

По теореме Гаусса

Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
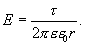
| (13.13) |
Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).

Суммарный поток вектора; напряженности равен вектору  , умноженному на площадь S первого основания, плюс поток вектора
, умноженному на площадь S первого основания, плюс поток вектора  через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,
через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,  С другой стороны по теореме Гаусса
С другой стороны по теореме Гаусса

Следовательно

но  тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна

| (13.14) |
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
13. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ.
Электрический диполь— система двух равных по модулю разноименных точечных зарядов (  ), расстояние
), расстояние  между которыми значительно меньше расстояния до рассматриваемых точек поля.
между которыми значительно меньше расстояния до рассматриваемых точек поля.
Плечо диполя — вектор  , направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между зарядами.
, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между зарядами.
Электрический момент диполя (дипольный момент):
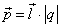 .
.
Потенциал поля диполя:

Напряженность поля диполя в произвольной точке (согласно принципу суперпозиции):

где 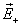 и
и 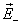 — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами.
— напряженности полей, создаваемых соответственно положительным и отрицательным зарядами.

Напряженность поля диполя на продолжении оси диполя в точке А:
 .
.
Напряженность поля диполя на перпендикуляре, восставленном к оси из его середины в точке B:
 .
.

|
из
5.00
|
Обсуждение в статье: Напряженность электрического поля произвольного распределения зарядов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

